IB Docs (2) Team
Paired sample t-tests
When writing the IA, nothing seems to worry students (and teachers) more than the application of inferential statistics. And yet - it is actually not as difficult as it may seem.
The paired sample t-test is used when we have a repeated measures design. The t-test is used with larger sample sizes. Using the t-test with smaller sample sizes may lead to a Type I error - that is, the rejection of a true null hypothesis. If you have a sample size smaller than 30, you should test the normality of the distribution of your data before carrying out the t-test; otherwise, the use of the test is not justified.
- The study uses a repeated measures design.
- The data is quantitative and at the interval or ratio level of data.
- The sample size is 30 or more. It is recommended for the IA in psychology that the Wilcoxon Signed Ranks test be used instead of a t-test for sample sizes lower than 30.
- The data is normally distributed. In sample sizes less than 30, evidence of normal distribution should be provided to justify the use of the t-test.
A sample IA
One of the commonly done internal assessment replications is the study done by Stroop (1966).
In this replication of the study, there are two conditions. In condition 1 (T1), participants were asked to read the list of words in the image to the left. In this case, there was no cognitive interference. In condition 2 (T2), the participants were asked to name the "colour of the word." This task has a high level of cognitive interference. The task of reading is an associative task - that is, it is our normal inclination to read a word, not identify its colour!
Let's say that we have a sample of 20 participants. The chart below shows the data for this experiment. The unit of the data is the number of seconds it took the participant to complete the task.
| T1 | 10.5 | 9.8 | 7.6 | 8.9 | 10.8 | 12.5 | 7.2 | 8.9 | 9.5 | 10.4 |
| T2 | 15.4 | 10.9 | 11.6 | 13.5 | 13.8 | 15.0 | 11.8 | 12.1 | 13.5 | 12.0 |
| T1 | 11.3 | 9.4 | 7.0 | 8.8 | 12.1 | 9.7 | 8.5 | 7.6 | 10.3 | 9.9 |
| T2 | 15.6 | 12.1 | 9.5 | 11.6 | 16.8 | 14.4 | 12.1 | 9.5 | 13.8 | 12.7 |
The mean for Condition 1 is 9.535 seconds with a median of 9.6. The standard deviation of the data is 1.528
The mean for Condition 2 is 12.885 with a median of 12.4. The standard deviation of the data is 1.949.
The question is - is there a significant difference between the average time taken when simply reading the words and identifying the colour of the words?
First, we need to find out if our data is normally distributed.
Checking for a normal distribution
The Central Limit Theorem assumes that the larger the sample, the more likely we are to have a normal distribution. Here is an explanation of the theorem. (Students studying statistics in IB math probably already know about this theorem!)
The general guidance for a normal distribution is to have a sample of 30 or more. However, the t-test may be used with smaller samples if we can show that the sample is normally distributed. How do we do this?
The test for normality is called the Kolmogorov-Smirnov test [K-S]. It is designed to test normality by comparing your data to a normal distribution with the same mean and standard deviation as your sample. If the test is NOT significant, then the data are normal, so any value above .05 indicates normality.
The easiest way to do this test is to use an online calculator. A good example can be found here.
When you click on the link, enter your data for each group into the boxes, separating the data by commas. Your data entry should look like the image below.
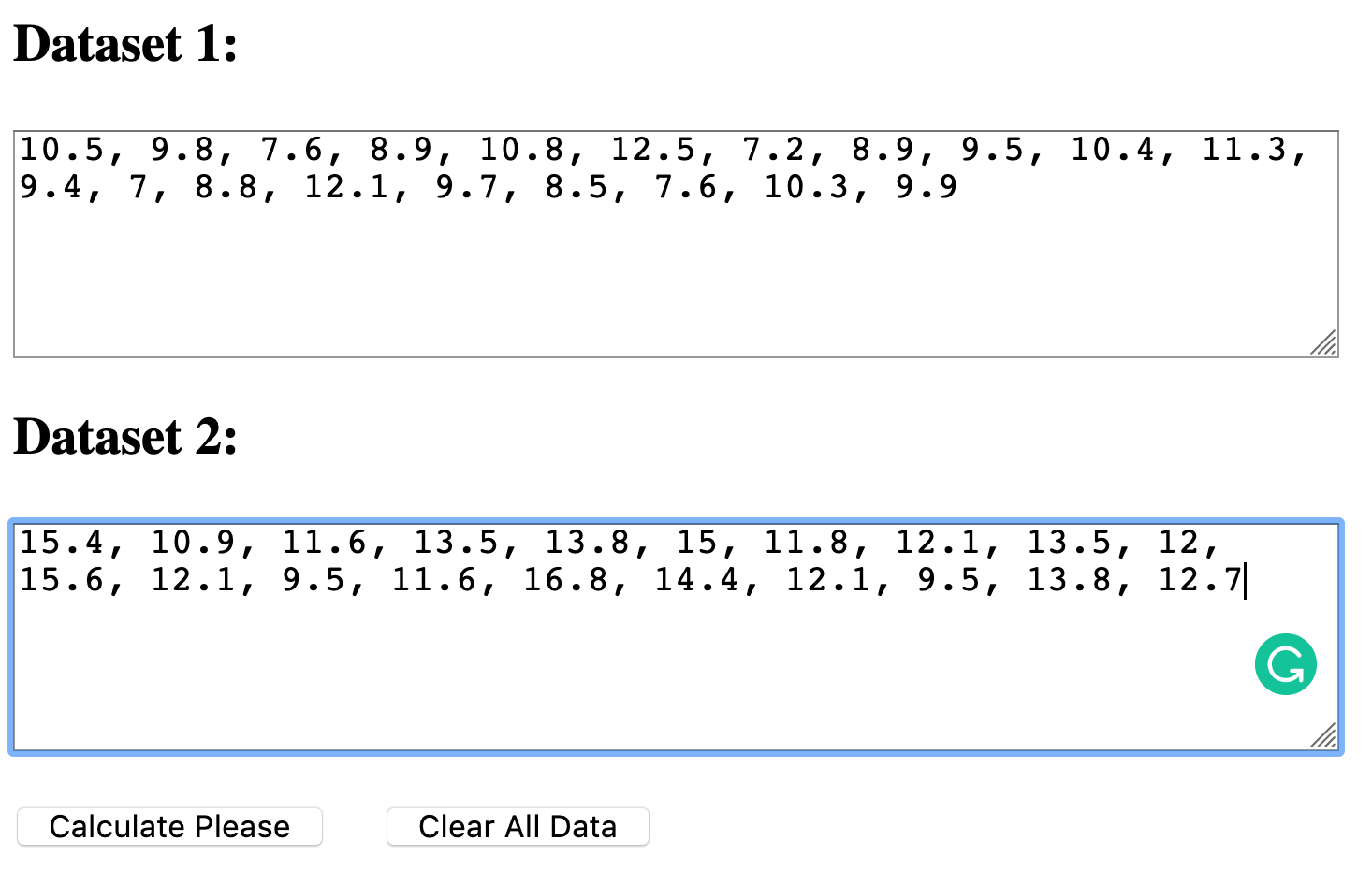You then press "calculate please." If your data is normally distributed, as is the case here, you will get a message that confirms that for each of the two conditions. This evidence should be included in your report as follows:
We carried out a Kolmogorov-Smirnov test to see if the data is consistent with a normal distribution. Both conditions were normally distributed. In the no interference condition, p = 0.99; In the interference condition, p = 0.72. Therefore, it is justified to carry out a t-test.
If the test tells you that the sample is not normally distributed, you should run a Wilcoxon signed ranks test.
Calculating the paired-sample t-test
The t-test is quite a complex test to calculate by hand. For this page, we will use the calculator on Social Science Statistics to determine the p-value of the data above.
When you open the calculator, you should see that it says: T-Test Calculator for 2 Dependent Means.
Click on "Take me to the calculator!"
Enter your data into the two boxes. It is easy to just copy and paste from a spreadsheet.
Remember to click on "one-tailed" test. The convention is to also choose 0.05 as the p-value. The reason for this is that if the results are not significant 0.05, they will not significant at any level.
When you press calculate, you will see that the results are significant and a more precise p-value is given. The statement of significance is in blue.
The value of t is 13.371878. The value of p is < .00001.
You should print the entire page of the calculation and include it in an appendix of your IA.
Reporting the statistics
We can see from the table above that our results are significant. We can reject the hypothesis. It appears that the interference task did have a significant effect on the time taken to read the list of words. So, how do we write our statement of findings?
When reporting the results of a t-test, the correct way to report them is as follows:
t(degrees of freedom) = the t statistic, p = p-value.
Degrees of freedom = n - 1.
So, using our example above, the statement of the findings would read as follows:
There was a significant increase in the time taken to read the words on this list in the interference condition (M = 12.885, SD = 1.949) compared to the non-interference condition (M = 9.535, SD = 1.528), t(19) = 13.37, p = .00001.
P-values
Often people will tell you that you should only report p ≤ 0.05, 0.01, 0.001 - and that you should not report the exact p-value. Although that used to be true when we had to use critical values tables in the back of statistics books to determine whether our data are significant, this is no longer the case.
According to the 6th edition of the APA style manual, "when reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p ≤ .001." (p. 114)
Twitter
Facebook
LinkedIn