IA marking: Sample 1
 The sample below is based on Strack and Mussweiler's (1997) study of anchoring bias.
The sample below is based on Strack and Mussweiler's (1997) study of anchoring bias.
The sample is based on a student's work, but is heavily edited and changes have been made to illustrate different facets of the IA.
The appendices do not include the letter of consent, materials, or the debriefing notes. The appendices do include the raw data and statistical calculations. Failure to include raw data or statistical calculations is penalized in the analysis.
Introduction
Human beings are cognitive misers. We often make decisions based on a minimal amount of effort, rather than having to do a lot of research to make a decision. However, this is not always true. If we are going to buy a house or a new car, we will often do research to find out what is the best quality car for the money that we can spend. Often when making less important decisions, we use information that is readily available in order to make a decision.
Stanovich and West (2000) proposed the Dual Process Model of thinking and decision making. They argue that there are two types of thinking - System 1 and System 2 thinking. System 1 thinking is automatic and the "default system." It is more prone to errors because it bases decisions on immediately available information and past experience. System 2 thinking is more reasoned and requires more effort. System 1 uses mental shortcuts called "heuristics."
One example of a heuristic is the anchoring effect. The anchoring effect is defined as a "biased estimate toward an arbitrary value considered by judges before making a numerical estimate" (Jacowitz and Kahnemann as cited in Stack and Mussweiler, 1997 p 437). According to Strack and Mussweiler, the anchoring effect occurs when there is only general knowledge about the value of something and little information besides the anchor value is provided (p 438).
The study we are going to replicate was carried out by Strack & Mussweiler (1997). The original study was carried out on 69 German university students. The students were asked to sit at one of four computer terminals and answer a series of questions. The question was "Did Mahatma Gandhi die before or after the age of X?" The second question was "How old was he when he died?" Each computer terminal, however, had a different suggested age. The anchor values were implausible, low anchor (9); implausible, high anchor (140); a plausible low anchor (64); plausible, high anchor (79).
The researchers found that the plausible anchors had a clear effect on the estimates of the participants, with the high anchor value resulting in a mean of 99.6 years and the low anchor value a mean of 67.9. The Implausible low anchor had a greater effect than the implausible low anchor, with values of 50.1 and 66.7 respectively.
We decided to replicate this study, but changing the famous person to Michael Jackson, someone we thought that our population would know better. We also decided to have a control to see what age would be predicted without an anchor, something that was lacking from the original study. To keep our experiment simple, we decided to only investigate the effect of a high anchor on the estimates made by the participants. According to the Dual Process model, a lack of information about Michael Jackson will lead to the participants using the anchor to estimate his age at the time of death.
The aim of our study was to determine if a high anchor value would affect the estimated age of death of Michael Jackson in a high school student population. The IV will be the presence of an anchor value; the DV will be the estimation of the age of Michael Jackson’s death.
Null Hypothesis: There will be no significant difference between high school students' estimated age at which Michael Jackson died in relation to a presented anchor value or no anchor.
Research Hypothesis: High school students who are presented with a high anchor value for Michael Jackson’s age at death will estimate a higher value than those without an anchor value.
Exploration
The research design used was a lab experiment where the independent variable was manipulated. This was used so that an independent variable could be manipulated and a dependent variable measured to establish a cause and effect relationship. In order to test anchoring bias, the participants were deceived as to the true purpose of the experiment prior to it happening to avoid demand characteristics. An independent samples design was used as different participants were used for each treatment of this experiment, each group was given a different treatment to test the hypothesis.
An opportunity sample of 27 high school psychology students aged 17 and 18 was used. The students were all first-year students and had only been in the course for one month. It is unlikely that they would have known the goal of the experiment.
The experiment was prompted with the question “How old was Michael Jackson when he died?” for both groups. The only difference was in the independent variable of changing the age anchor, where for one group no anchor was proposed, and for the other, the second group was asked a second part of the question, "I think that he might have been around 75 years old. What do you think?" This second condition served as a control group so that we could see what the baseline estimate would be without an anchor.
The materials used for this was just pen and paper. Another controlled variable was in that the participants were not allowed to communicate with each other in order to avoid other variables that could contribute to influencing the guess.
Analysis
Table 1. Descriptive analysis of data
| No anchor | High anchor | |
| Mean | 43.3 | 51.7 |
| Median | 43.5 | 51 |
| Mode | 52 | 58 |
| Standard deviation | 8.19 | 7.73 |
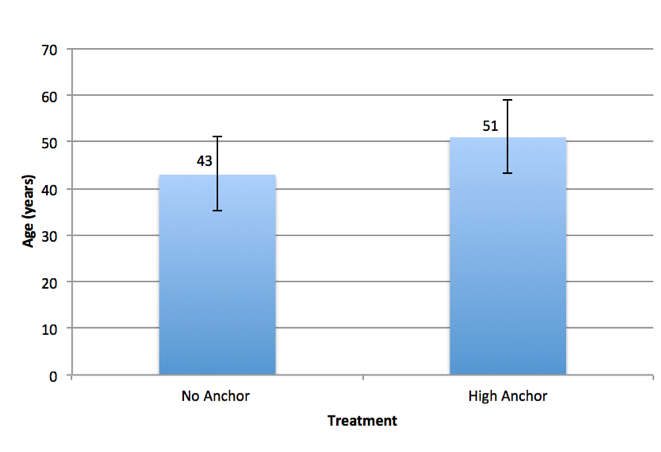
The raw data (see appendix i) shows that there were no obvious outliers in the data. The average estimate by the high anchor group is 8.4 years higher than the no anchor group. The standard deviations of the two groups are very similar. The median for both groups is very similar to the mean. This indicates that outliers are unlikely to have distorted the mean values.
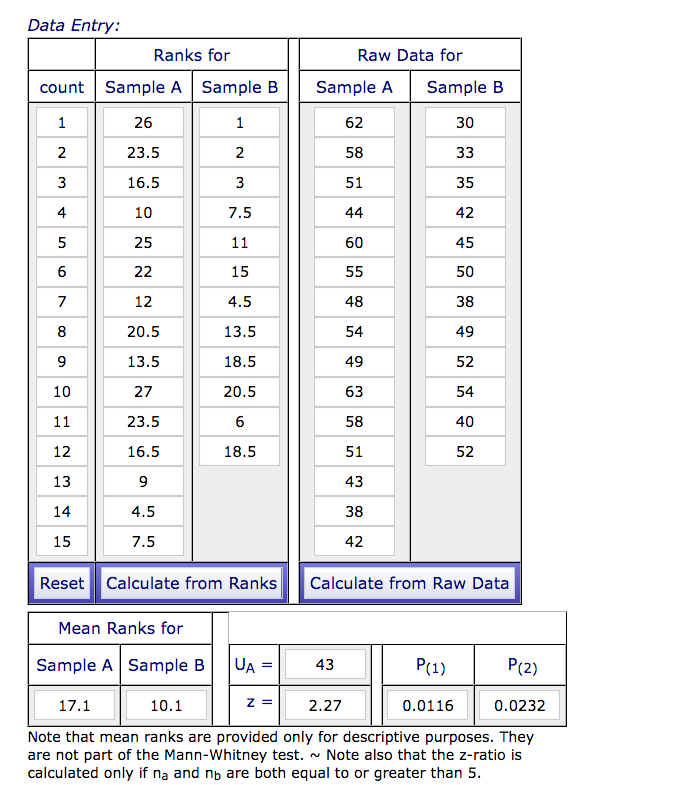
To test for significance, a Mann Whitney U test (see appendix ii) was performed. This was done because of the size of the sample and our data was at least ordinal. The data can be deemed significant as the p-value was 0.0116 for a one-tailed test, which is below the 0.05 value required for significance. This means that we can reject the null hypothesis. It appears that the presence of an anchor did have an effect on the estimates made by the students.
Figure 1: Graphic representation of mean age estimates by participants in relation to no and high anchor
Evaluation
This experiment examined the use of heuristics by students to take mental “shortcuts” when making quick decisions. This is an example of System 1 thinking, which uses an automatic and intuitive way of thinking rather than a more conscious and rational way of thinking known as System 2. The reason why heuristics occur is the System 1 tendency to rely on limited amounts of information in order to make intuitive and quick answers, and not consider the full picture.
Our results reflect the theory about anchoring effect as explained by Stracker and Mussweiler. Although the students would have some general knowledge about JFK, they would not know how old he was when he was killed. Therefore, it is highly likely that they would use an anchor to make a decision. This is precisely how System 1 thinking operates; it takes into account the information available - in this, the high anchor - and makes a decision without an extended amount of effort.
One of the strengths on the procedure was that the students had only 30 seconds to write down an answer; this prevented possible System 2 thinking where they might consider critical thinking regarding the plausibility of the anchor itself and perhaps avoiding the cognitive bias altogether. Another strength was the independent samples design, as this experiment relies on the participant not being able to discern the purpose of the experiment. It would not have been possible to do this as a repeated measures design as the participants would have figured out the aim and shown demand characteristics. Finally, the use of the no-anchor condition was helpful as it creates a baseline value that the results of the high-anchor condition can be compared to.
However, there was a limitation in our sample, as high school students were used, so they might not have known much about Michael Jackson; as psychology students, they may have been more likely to guess the goal of the experiment. There was also an issue with the number of participants for each group as although the difference was only by 4 students, in such a small sample, it can create a gap in reliability to how differing the two groups really were.
As a possible modification for this experiment, the experiment should have an equal number of participants for each of the treatments. In order to more rigorously test for the effects of the anchoring effect, it would be better to have three groups, where there could be a comparison drawn between a low anchor, a high anchor, and no anchor. This could thus make a more statistically significant analysis if there is, in fact, a deviation from the mean of the control group in either direction.
In conclusion, we are able to reject the null hypothesis at p ≤ 0.01. It appears that a high anchor does affect students' estimates of the age of death of Michael Jackson.
Works cited
Stanovich, K. E., & West, R. F. (2000). Individual Differences in Reasoning: Implications for the Rationality Debate? Heuristics and Biases, 421-440. doi :10.1017/cbo9780511808098.026
Strack, F. and Mussweiler, T., (1997). Explaining the Enigmatic Anchoring Effect: Mechanisms of Selective Accessibility. Journal of Personality and Social Psychology, Vol. 73, No. 3, 437-446.
Appendix i. Raw data
Student estimates of the age of John F. Kennedy’s death in relation to an anchor value.
| No anchor | 30 | 33 | 35 | 42 | 45 | 50 | 38 | 49 | 52 | 54 | 52 | 40 | |||
| High anchor | 62 | 58 | 51 | 44 | 60 | 55 | 48 | 54 | 49 | 63 | 58 | 51 | 43 | 38 | 42 |
Appendix ii. Mann Whitney calculations
Assessment
Introduction (max 6 marks)
The theory or model upon which the student’s investigation is based is described and linked to the study. The aim of the investigation is stated; there is no explanation of the relevance of the aim. The independent and dependent variables are stated and operationalized in the null and research hypotheses.
4 marks
Exploration (max 4 marks)
The research design is identified, but not well explained. The sampling technique is identified and described, but how it was actually obtained is not explained. The characteristics of the sample are not described. The use of a control group is explained. There is a very limited description of the materials. The choice of Michael Jackson is explained, but in the introduction, not in the exploration.
2 marks
Analysis (max 6 marks)
Descriptive and inferential statistics are appropriately and accurately applied; however, the candidate states that there are no outliers in the raw data with no evidence to back up this claim. Calculations for outliers should have been included in the appendices. In addition, the mode and median are not discussed but are included in the table. The graph is correctly presented and addresses the hypothesis. The statistical findings are interpreted with regard to the data and linked to the hypothesis, but could have been more developed.
5 marks
Evaluation (max 6 marks)
The findings of the student’s investigation are clearly linked to the background theory or model and anchoring bias. The evaluation lacks limitations of the design, strengths of the sample and an evaluation of the procedure. The comment that the size of the two groups was not equal is not a valid limitation of the sample or design. This does not have a true effect on the data and is often the case when participants are randomly allocated to conditions. Modifications are not appropriate or relevant.
3 marks
Total marks

 IB Docs (2) Team
IB Docs (2) Team
