IB Docs (2) Team
Binomial Sign Test
When writing the IA, nothing seems to worry students (and teachers) more than the application of inferential statistics. And yet - it is actually not as difficult as it may seem.
The binomial sign test is used when we have a repeated measures design. There are very few studies that are replicated for IA that would make use of the binomial sign test. Most of the studies that obtain nominal data use an independent sample design and require the use of a chi-squared. However, there are some examples that require this test. One of the most common is replications of Griggs and Cox (1982).
- The research design is repeated measures
- The data is nominal
- The data is at a higher level than nominal, but due to a skewed distribution, a test of lower power is needed.
When using a binomial sign test, the graph should represent the frequencies of the conditions.
A Sample IA
Griggs and Cox (1982) wanted to see what would happen if they added more context to the Wason Selection Test. Research has shown that even when being taught how to do the Wason Selection Test, people continued to make errors. Their argument is that it was perhaps the artificial nature of the task - and that perhaps with more context, participants would answer the question correctly more frequently.
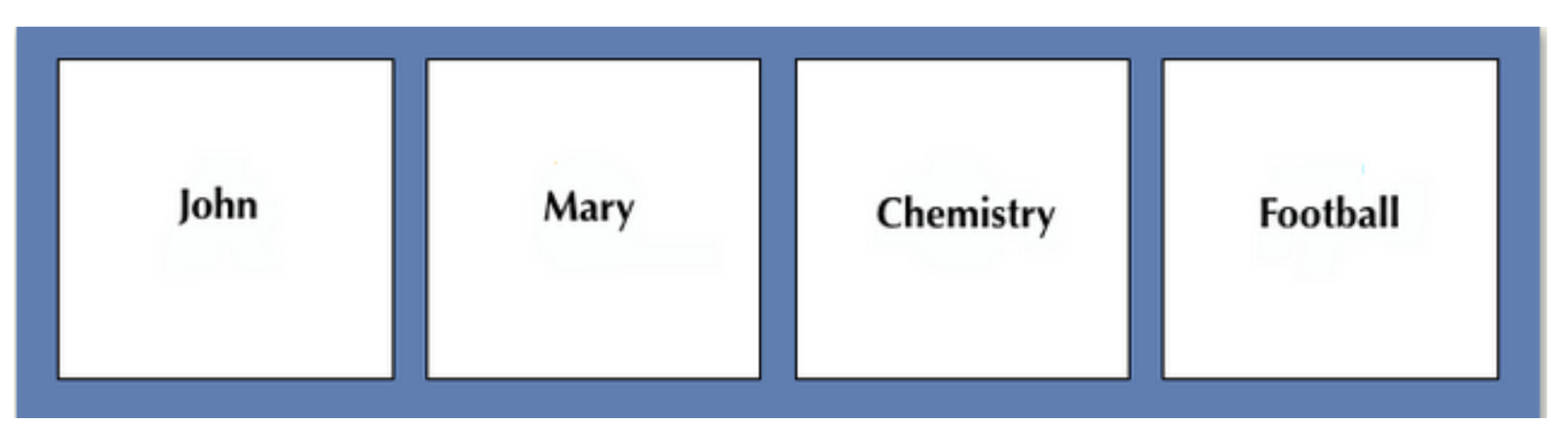
The first task was without any context. Here is an example.
If there is a male's name on one side of the card, then there is an IB subject on the other side of the card. Select those cards that you definitely need to turn over to determine whether or not the cards are violating the rule.
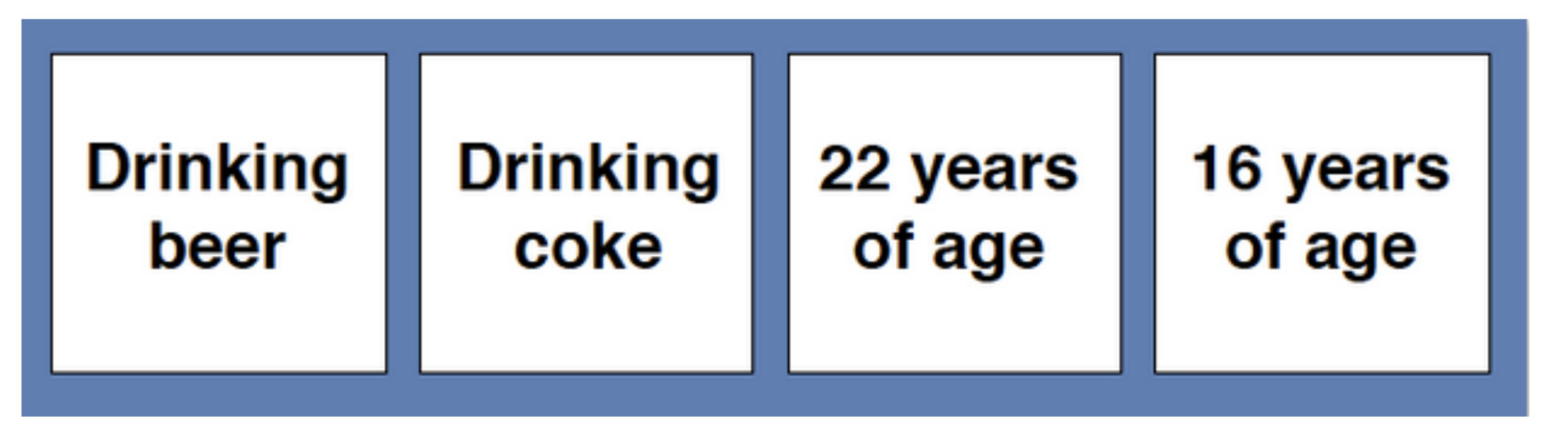
The second task was with context. Here is an example.
Imagine you are a police officer on duty. It is your job to ensure that people conform to certain rules. The cards below have information about four people sitting at a table. On one side of a card is a person's age and on the other side of the card is what a person is drinking. Here is a rule: if a person is drinking beer, then the person must be over 18. Select those cards that you definitely need to turn over to determine whether or not the people are violating the rule.
For the first one, the answer is John and Football.
For the second one, the answer is Drinking beer and 16 years of age.
What we want to find out is - is there a significant difference in individual performance on the two tasks? Did the presence of context make a significant difference?
Calculating the binomial sign test
In each condition, the participant will either get the question “correct” or “incorrect.” This is nominal data.
Let's say that we have 16 participants. Here were their results. If the participant answered correctly, this is indicated by 1; if the participant answered incorrectly, this is indicated by 0.
| No context | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| Context | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| Difference | + | 0 | + | 0 | - | + | + | - | 0 | 0 | + | + | 0 | - | + | 0 |
You will see that in the no context condition, 7 participants answered correctly. In the context condition, 11 participants answered correctly. However, since this is a repeated measures design, simply getting the frequency of correct responses is not enough. We want to know how many participants in our sample were not able to solve the problem correctly without context but were able to solve it when context was provided. And whether the number of these participants is significant based on the size of our sample.
This is where the binomial sign test comes in.
The final row of the table has the label “difference.” If the participants answered incorrectly in the "no context" condition and then correctly in the "context" condition, then the difference is noted as a plus. If the participant answered correctly in the "no context" condition and then incorrectly in the "context" condition, then the difference is noted as a minus. If the answered either correctly in both conditions or incorrectly in both conditions, then the difference is zero.
To calculate the binomial sign test, you have to count all the + values and all the - values.
n(+) = 7 n(-) = 3
The statistic disregards all data where the difference between the two conditions is zero. To find the new sample size, you add n(+) and n(-). In this case, the total is 10.
To determine whether the results are significant, we use the lower value - in this case, 3.
Then we consult the table below. Notice that you cannot have significant results if your adjusted value of n is less than 8. So, if most participants had done both tasks either correctly or incorrectly and our new sample size was below 8, you could keep the null hypothesis - your results would not be significant.
Remember that our new value for n is 10. Looking at the critical values for 10, if we have a value below 1, then our data is significant. Our lower value, which is n(-) = 3 exceeds this value, so we are not able to reject our null hypothesis. We will retain the null hypothesis. It appears that in this study, the results are not significant - context played no significant role in the participants' ability to solve the Wason selection test.
When reporting the binomial sign test results, the statement should look like this:
For each participant an improvement in performance on the Wason Selection test was recorded as positive, whereas a decrease in performance was recorded as negative. Six participants' performance was the same under both conditions and this result was omitted from the analysis. The remaining ten results were submitted to a binomial sign test and the rate of improvement over decrease in performance with the presence of context was found to not be significant, S (n = 10), p > 0.05.
Twitter
Facebook
LinkedIn