InThinking Revision Sites

INTHINKING REVISION SITES

Own your learning

Why not also try our independent learning self-study & revision websites for students?

We currenly offer the following DP Sites: Biology, Chemistry, English A Lang & Lit, Maths A&A, Maths A&I, Physics, Spanish B

"The site is great for revising the basic understandings of each topic quickly. Especially since you are able to test yourself at the end of each page and easily see where yo need to improve."

"It is life saving... I am passing IB because of this site!"

Basic (limited access) subscriptions are FREE. Check them out at:

www.StudyIB.net

Chi squared: Practice problems

  • /
  • Statistics/
  • Chi squared: Practice problems

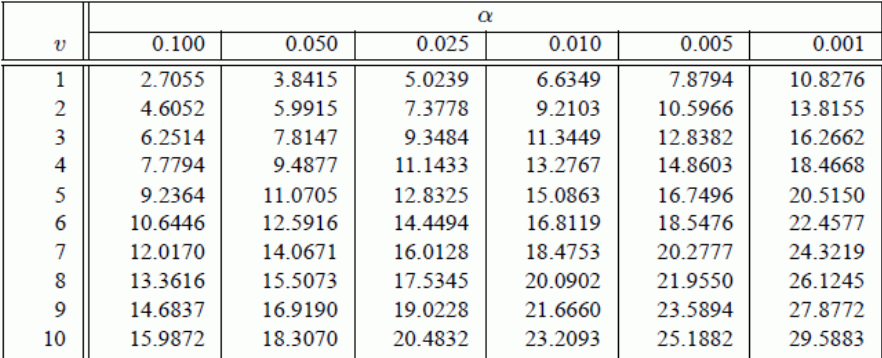
Below you will find three problems that are based on research that you may study in the IB psychology course.  For each problem, decide whether the data is significant by applying the chi-squared of difference. You may either do the problems by hand or use the chi-square calculator. If you are calculating the chi-squared by hand, you will need to use the following critical values table.  Remember, the value in the first column is the degrees of freedom.

Problem 1. Snacking habits in men and women.

In a study in health psychology, they wanted to see if there are gender differences in one’s choice of high fat, high protein or high sugar foods when choosing a snack.  The sample was made up of 42 men and 36 women.  The results are below:

Type of snackMen Women
High fat812
High protein218
High sugar1316

Please note that there are three different choices here, so the degrees of freedom will be different from the example above.

Type of snackMen Women
High fatfo  = 8; fe = 10.77fo  =  12; fe = 9.23
High proteinfo  =  21; fe = 15.62fo  =  8; fe = 13.38
High sugarfo  =  13; fe = 15.62fo  =  16; fe = 13.38

If you then calculate the sum of all (fo-fe)2, you get a chi-square value of 6.51

The degrees of freedom are equal to the number of columns minus 1 (2 -1) times the number of rows minus 1 (3 - 1) - or 2 degrees of freedom.

If you look in the row for 2 degrees of freedom, you see that you need to have a chi-square value of at least 5.99 to have significant results (p ≤ 0.05)  This is the case.  If you go over to the next column, you see that you need a score of 7.377 to get a significance level of p ≤ 0.025.  This is not the case.  So, we can reject the null hypothesis at p ≤ 0.05.

Problem 2. Training people to be more prosocial

A study by Beaman et al wanted to see if giving a lecture on helping behaviour would lead to a person helping someone a week later in a staged helping scenario.  There were 80 participants.  40 of the participants listened to a lecture on helping research, including videos of the original studies.  The other 40 participants were given a lecture on obesity and emotions - in other words, a study not focused on helping. In the helping lecture, 17 of the participants helped.  In the control condition - the obesity lecture - 10 of the participants helped. Is this a significant difference?

ResponseHelping lectureNo helping lectureTotals
Helpedfo  = 17; fe = 13.5fo  = 10; fe = 13.527
Did not helpfo  = 23; fe = 26.5fo  = 30; fe = 26.553
Totals4040n = 80

If you then calculate the sum of all (fo-fe)2, you get a chi-square value of 2.73

The degrees of freedom is equal to the number of columns - 1 (2 -1) times the number of rows minus 1 (2 - 1) - or 1 degree of freedom.

If you look in the row for 1 degree of freedom, you see that you need to have a chi-square value of at least 3.8415 to have significant results (p ≤ 0.05)  This is not the case.  In this case, we would have to retain the null hypothesis.  There does not seem to be any significant difference in the frequency of helping behaviour based on whether or not the participants heard a lecture on helping research.

Problem 3: Studies of attraction

In a replication of a study by Dion wanted to see if the attractiveness of an individual would lead to female participants automatically assigning positive or negative traits to an individual. The participants were shown three different photos: an attractive male, an average-looking male, and an unattractive male.   They were then given a set of traits and asked to rate the male on those traits. This gave a composite score that was either “positive”, “negative” or “neutral.”  There were 200 participants.  The final scores are below. Is this a significant finding?

Personality ratingUnattractiveAverage attractionAttractive
Positive personality616594
Neutral personality655456
Negative personality748150

Notice that for this one, there are three columns and three rows!

Personality ratingUnattractiveAverage attractionAttractive
Positive personalityfo  = 61; fe = 73.33fo  = 65; fe = 73.33fo  = 94; fe = 73.33
Neutral personalityfo  = 65; fe = 58.33fo  = 54; fe = 58.33fo  = 56; fe = 58.33
Negative personalityfo  = 74; fe = 68.33fo  = 81; fe = 68.33fo  = 50; fe = 68.33

If you then calculate the sum of all (fo-fe)2, you get a chi-square value of 17.75

The degrees of freedom is equal to the number of columns - 1 (3 -1) times the number of rows minus 1 (3 - 1) - or 4 degrees of freedom.

If you look in the row for 4 degrees of freedom, you see that you need to have a chi-square value of at least 9.48 to have significant results (p ≤ 0.05)  This is the case.  Now you look at the column for p ≤ 0.025. The critical value is 11.344.  The chi-square value is higher than that. Finally, we look at the column for p ≤ 0.01. The critical value is 13.27.  Once again, our chi-squared value is higher.  Therefore, we can reject the null hypothesis at p ≤ 0.01.  It appears that one's level of attractiveness has a significant impact on the perceived personality.