DP Mathematics: Analysis and Approaches Questionbank

Topic 3— Geometry and trigonometry
Description
[N/A]Directly related questions
-
20N.2.AHL.TZ0.H_10a:
Given that meets at the point , find the coordinates of .
-
20N.1.SL.TZ0.S_7b:
Particle also moves in a straight line. The position of is given by .
The speed of is greater than the speed of when .
Find the value of .
-
EXN.2.SL.TZ0.2a:
Show that arc has length .
-
21M.2.SL.TZ1.4:
A Ferris wheel with diameter metres rotates at a constant speed. The lowest point on the wheel is metres above the ground, as shown on the following diagram. is a point on the wheel. The wheel starts moving with at the lowest point and completes one revolution in minutes.
The height, metres, of above the ground after minutes is given by , where .
Find the values of , and .
-
21M.2.SL.TZ2.7e:
If the observer stands directly under point for one minute, point will pass over his head times.
Find the value of .
-
21M.2.AHL.TZ2.12a:
Show that is an even function.
-
19M.1.SL.TZ1.S_3a:
Given that , find the value of .
-
21N.2.SL.TZ0.8a:
Show that .
-
21N.2.AHL.TZ0.7a:
Determine the value of .
-
21N.2.AHL.TZ0.9a:
Show that .
-
22M.2.AHL.TZ1.7b:
Given that is a minimum, find .
-
22M.2.SL.TZ2.7d:
Find the distance from point to point .
-
22M.2.SL.TZ2.7a:
Find the distance from point to point .
-
22M.2.AHL.TZ2.11d.ii:
Determine the length of time between the first airplane arriving at and the second airplane arriving at .
-
22M.2.SL.TZ1.3b:
Given that the area of the logo is , find the value of .
-
22M.2.SL.TZ2.1b:
Find the area of the shaded sector.
-
EXM.3.AHL.TZ0.5a.ii:
Write down the amplitude of this graph
-
EXM.3.AHL.TZ0.5f.i:
Show that .
-
EXM.3.AHL.TZ0.5e.iii:
.
-
EXM.3.AHL.TZ0.5d:
By considering the graph of , find the value of , , and .
-
17N.1.SL.TZ0.T_10a:
Find the length of EB.
-
19M.1.SL.TZ1.T_10b:
Find the area, in km2, of triangle ABC.
-
19M.1.AHL.TZ1.H_9a:
Show that .
-
18M.1.SL.TZ1.T_14c:
Calculate the curved surface area of the remaining solid.
-
18M.2.AHL.TZ1.H_3:
Let where .
Express in terms of sin and cos .
-
19M.2.AHL.TZ1.H_10b:
Write down two transformations that will transform the graph of onto the graph of .
-
19M.2.AHL.TZ1.H_10e:
Find (0.007).
-
18M.2.AHL.TZ2.H_4b:
Find the area of the shaded region.
-
18M.1.SL.TZ2.S_4:
The following diagram shows a circle with centre O and radius r cm.
The points A and B lie on the circumference of the circle, and = θ. The area of the shaded sector AOB is 12 cm2 and the length of arc AB is 6 cm.
Find the value of r.
-
19M.2.SL.TZ2.T_2a:
Find the distance from A to C.
-
16N.2.SL.TZ0.T_5a:
the length of BD;
-
19M.2.SL.TZ2.S_4b:
Find the area of triangle OBC in terms of and θ.
-
17N.2.AHL.TZ0.H_11b.ii:
Express in terms of .
-
17N.2.AHL.TZ0.H_11b.iii:
Hence show that can be expressed as .
-
17M.2.AHL.TZ1.H_8a:
Find an expression for the volume of water in the trough in terms of .
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
16N.2.SL.TZ0.T_6e:
Find .
-
17M.1.SL.TZ2.T_12a:
Find the volume of water in the container.
-
18M.2.SL.TZ2.T_5a.ii:
Use Giovanni's diagram to calculate the length of AX.
-
18M.2.SL.TZ2.T_5c:
Giovanni adds a point D to his diagram, such that BD = 45 m, and another triangle is formed.
Find the angle of elevation of A from D.
-
19M.2.SL.TZ2.T_3b:
Find the slant height of the cone-shaped container.
-
17M.2.SL.TZ2.S_1a:
Find the length of arc ABC.
-
16N.2.SL.TZ0.S_10b:
(i) Write down the value of .
(ii) Find .
-
17N.2.SL.TZ0.S_10a:
Show that .
-
18M.2.SL.TZ1.S_10b.ii:
For the graph of , write down the period.
-
18M.2.SL.TZ1.S_10c:
Hence, write in the form .
-
17M.1.SL.TZ1.T_13a:
Find the length of BC.
-
18N.1.SL.TZ0.T_1b:
Write down your answer to part (a) correct to the nearest integer.
-
18M.1.AHL.TZ1.H_10e:
Find the area of the triangle OPQ.
-
17N.1.AHL.TZ0.H_9a.ii:
Find, in terms of a and b .
-
18N.1.AHL.TZ0.H_9b:
Find, in terms of , the equation of the line L which passes through M and is perpendicular to the plane П.
-
17M.2.AHL.TZ2.H_7:
Given that a b b c 0 prove that a c sb where s is a scalar.
-
19M.2.SL.TZ2.S_7:
The vector equation of line is given by r .
Point P is the point on that is closest to the origin. Find the coordinates of P.
-
16N.1.AHL.TZ0.H_8a:
find the value of ;
-
19N.1.AHL.TZ0.H_3:
Three planes have equations:
, where .
Find the set of values of and such that the three planes have no points of intersection.
-
19N.1.AHL.TZ0.H_8:
A straight line, , has vector equation r .
The plane , has equation .
Show that the angle between and is independent of both and .
-
SPM.3.AHL.TZ0.2h.ii:
Hence express as a cubic polynomial.
-
SPM.3.AHL.TZ0.2h.i:
Hence show that , .
-
18M.2.SL.TZ2.S_8a.i:
Find .
-
17N.2.SL.TZ0.S_1b:
Find the area of triangle ABC.
-
18M.2.SL.TZ2.S_8a.ii:
Find .
-
18M.2.SL.TZ2.S_8b:
Find the angle between PQ and PR.
-
18M.2.SL.TZ2.S_2b:
Find DC.
-
19M.1.SL.TZ1.S_3c:
Hence or otherwise, find .
-
18N.2.SL.TZ0.S_8c:
Find the angle between and .
-
18N.2.AHL.TZ0.H_11b:
Show that .
-
17M.2.SL.TZ1.S_8b.iii:
Find the value of .
-
18M.2.SL.TZ2.S_2a:
Find DB.
-
18N.2.AHL.TZ0.H_11c:
By sketching the graph of as a function of , determine the range of values of for which there are possible values of .
-
17M.1.SL.TZ2.S_7:
Solve , for .
-
20N.2.AHL.TZ0.H_11b:
Find an expression for in terms of .
-
20N.2.AHL.TZ0.H_11d:
Find the total distance travelled by in the first seconds of its motion.
-
20N.1.SL.TZ0.S_7a:
Find an expression for the velocity of at time .
-
20N.2.SL.TZ0.S_7b:
Find the value of when the area of the shaded region is equal to the area of sector .
-
20N.2.SL.TZ0.S_8a.ii:
Calculate the number of seconds it takes for the water wheel to complete one rotation.
-
20N.2.SL.TZ0.S_8c:
Find .
-
20N.2.SL.TZ0.T_3b:
Show that angle , correct to three significant figures.
-
21M.2.SL.TZ1.8e.i:
Find the size of .
-
EXN.1.AHL.TZ0.8a:
Show that and are never perpendicular to each other.
-
EXN.1.SL.TZ0.9d:
For the first 2 seconds of its motion, determine the amount of time that the ball is less than metres above the ground.
-
EXN.1.AHL.TZ0.8b.ii:
the condition on the value of .
-
21M.1.SL.TZ1.6a:
Show that .
-
21M.1.AHL.TZ1.11a.i:
Show that the point lies on .
-
21M.2.SL.TZ1.8d:
Hence, find the size of .
-
21M.1.SL.TZ2.8c:
Find the value of .
-
21M.3.AHL.TZ1.2c:
Show that .
-
21M.2.SL.TZ2.7a:
Given that point is metres from the base of the windmill, find the height of point above the ground.
-
21M.2.AHL.TZ2.12c.i:
Show that for .
-
21N.2.AHL.TZ0.9c:
Find the value of .
-
21N.2.AHL.TZ0.9e:
Find the height of the water at .
-
21N.2.AHL.TZ0.11b:
The line is the intersection of and . Verify that the vector equation of can be written as .
-
22M.2.AHL.TZ2.11d.i:
Find the coordinates of .
-
22M.2.AHL.TZ2.11c:
Find the acute angle between the two airplanes’ lines of flight. Give your answer in degrees.
-
22M.2.SL.TZ2.1a:
Find the length of the chord .
-
SPM.2.SL.TZ0.7b.ii:
Find the distance from the camp to point C.
-
SPM.2.SL.TZ0.9b.i:
Find the value of .
-
SPM.2.SL.TZ0.7d:
Find the bearing that Jacob must take to point C.
-
SPM.2.AHL.TZ0.12c:
Hence, or otherwise, show that the exact value of .
-
EXM.3.AHL.TZ0.5b.i:
Use your answers from part (a) to write down the value of , and .
-
17N.1.SL.TZ0.T_10c:
Find the vertical height of B above the ground.
-
19M.1.SL.TZ1.T_10a:
Find the size, in degrees, of angle BÂC.
-
19M.1.AHL.TZ1.H_4b:
Find the two possible values for the length of the third side.
-
19M.1.AHL.TZ2.H_9a:
Find the -coordinates of the points of intersection of the two graphs.
-
19M.2.AHL.TZ1.H_10d:
Find the total time in the interval 0 ≤ ≤ 0.02 for which ≥ 3.
-
17N.2.AHL.TZ0.H_11a.i:
Determine an expression for in terms of .
-
17N.1.SL.TZ0.S_4a:
Show that .
-
19M.2.SL.TZ1.S_8c.i:
Find the value of and of .
-
17M.1.AHL.TZ2.H_11a:
Solve .
-
18M.2.SL.TZ1.T_1c:
Calculate the length of MN.
-
19M.2.SL.TZ1.T_2e:
Olivia investigates arranging the panels, such that the longer edge of each panel is parallel to or .
State whether this new arrangement will allow Olivia to fit more solar panels to the roof. Justify your answer. -
19M.2.SL.TZ2.T_3a:
Find the volume of one cone-shaped container.
-
18N.1.SL.TZ0.T_9a.ii:
Calculate the volume of the paperweight.
-
17M.1.SL.TZ1.T_9b:
Find the slant height, , of the cone.
-
17M.2.SL.TZ2.T_4b:
Show that angle DBC is 48.7°, correct to three significant figures.
-
17M.2.SL.TZ2.T_4c:
Find the area of the park.
-
16N.2.SL.TZ0.S_10a:
(i) Find the value of .
(ii) Show that .
(iii) Find the value of .
-
17N.2.SL.TZ0.S_10c:
Show that the distance between the -coordinates of and is .
-
17M.1.SL.TZ1.S_8d.i:
Find a unit vector in the direction of .
-
19M.1.SL.TZ2.S_2a:
parallel.
-
17N.2.SL.TZ0.S_3a:
Find .
-
18N.1.SL.TZ0.T_1c:
Write down your answer to part (b) in the form a × 10k , where 1 ≤ a < 10 and k ∈ .
-
16N.1.SL.TZ0.T_7b:
Calculate the radius of the balloon following this increase.
-
18M.2.AHL.TZ1.H_11c.iii:
Find the distance between the two submarines at this time.
-
19M.1.AHL.TZ1.H_11a.i:
Find how many sets of four points can be selected which can form the vertices of a quadrilateral.
-
19M.1.AHL.TZ1.H_11a.ii:
Find how many sets of three points can be selected which can form the vertices of a triangle.
-
19M.1.AHL.TZ1.H_11c:
Write down the value of corresponding to the point .
-
19M.1.AHL.TZ1.H_11e:
Let be the point on with coordinates (1, 0, 1) and be the point on with parameter .
Find the area of the quadrilateral .
-
18M.1.AHL.TZ1.H_10a:
Find the Cartesian equation of the plane , passing through the points A , B and D.
-
17N.1.AHL.TZ0.H_9b.ii:
Find an expression for in terms of a, b and .
-
17N.1.AHL.TZ0.H_2a:
Find a vector equation of the line L passing through the points A and B.
-
17N.1.AHL.TZ0.H_2b:
Find the coordinates of the point of intersection of the line L with the plane Π.
-
17M.2.AHL.TZ2.H_9e:
Verify that 2j + k is perpendicular to the plane Π.
-
16N.1.AHL.TZ0.H_1:
Find the coordinates of the point of intersection of the planes defined by the equations and .
-
19N.1.AHL.TZ0.H_9b:
Show that .
-
19N.2.SL.TZ0.S_6:
The diagram below shows a triangular-based pyramid with base .
Edge is perpendicular to the edges and ., , , ,
Calculate
-
SPM.3.AHL.TZ0.2b.i:
local maximum points;
-
17N.1.SL.TZ0.S_9b:
Find the value of .
-
SPM.3.AHL.TZ0.2e:
Solve the equation and hence show that the stationary points on the graph of occur at where and 0 < < .
-
18N.1.AHL.TZ0.H_10a:
Use integration by parts to show that , .
-
19M.1.SL.TZ2.S_9d:
The following diagram shows the graph of for 0 ≤ ≤ 3. Line is a tangent to the graph of at point P.
Given that is parallel to , find the -coordinate of P.
-
19M.2.AHL.TZ2.H_3a:
Complete the given probability tree diagram for Iqbal’s three attempts, labelling each branch with the correct probability.
-
18N.2.SL.TZ0.S_8a.ii:
Find .
-
18N.1.AHL.TZ0.H_3b:
Write down the least value of such that has an inverse.
-
19M.2.AHL.TZ2.H_1:
In triangle ABC, AB = 5, BC = 14 and AC = 11.
Find all the interior angles of the triangle. Give your answers in degrees to one decimal place.
-
18N.2.AHL.TZ0.H_11a:
Find an expression for in terms of .
-
17M.1.SL.TZ1.S_10c:
Let , for . The graph of between and is rotated 360° about the -axis. Find the volume of the solid formed.
-
17M.1.SL.TZ1.S_10b:
Given that , find .
-
17M.2.AHL.TZ2.H_4b:
The triangle ABC is shown in the following diagram. Given that , find the range of possible values for AB.

-
19M.1.SL.TZ1.T_1c:
Find the volume, in cm3, of this calculator case.
-
EXN.1.SL.TZ0.9b:
Find the minimum height of the ball above the ground.
-
EXN.1.AHL.TZ0.12e:
Deduce a quadratic equation with integer coefficients, having roots and .
-
21M.2.AHL.TZ1.6b:
Find the coordinates of the point where , and intersect.
-
21M.1.AHL.TZ2.12b:
Show that where and .
-
21M.1.SL.TZ2.3a:
Show that the equation may be written in the form .
-
21M.1.SL.TZ2.3b:
Hence, solve the equation .
-
21M.2.SL.TZ2.7d:
Find the value of and the value of .
-
21M.2.AHL.TZ2.12f:
Sketch the graph of , clearly indicating any asymptotes with their equations and stating the values of any axes intercepts.
-
21N.2.AHL.TZ0.9b:
Find the value of .
-
21N.2.AHL.TZ0.7b:
Given that , determine the value of .
-
21N.2.AHL.TZ0.11a.ii:
Hence find the equation of , expressing your answer in the form , where .
-
22M.1.SL.TZ1.6a:
Describe these two transformations.
-
22M.2.SL.TZ1.3a:
Find the area of one of the shaded segments in terms of .
-
22M.2.SL.TZ1.7c:
Find the height of the pyramid, .
-
22M.2.AHL.TZ2.7a:
Show that a finite limit only exists for .
-
22M.2.AHL.TZ2.10b:
Find the values of when .
-
SPM.1.SL.TZ0.1b:
Find the area of triangle ABC.
-
SPM.2.SL.TZ0.9b.ii:
Hence, find the value of (6).
-
SPM.2.SL.TZ0.9c:
Find the value of and the value of .
-
EXM.3.AHL.TZ0.5b.ii:
Find the value of .
-
EXM.3.AHL.TZ0.5e.ii:
.
-
19M.1.AHL.TZ1.H_4a:
Show that .
-
18N.1.AHL.TZ0.H_11b.ii:
By writing as , find the value of cos in the form , where , and are integers to be determined.
-
18N.1.AHL.TZ0.H_11b.iii:
Hence, or otherwise, show that S = .
-
18M.2.SL.TZ1.S_3a:
Find the area of the shaded region, in terms of θ.
-
17N.2.SL.TZ0.T_6a:
Show that the volume of a cone shaped glass is , correct to 3 significant figures.
-
17N.2.SL.TZ0.T_6b:
Calculate the radius, , of a hemisphere shaped glass.
-
17N.2.SL.TZ0.T_6d:
Show that there is of orange paste in each special dessert.
-
18M.2.SL.TZ2.T_5a.i:
Use Giovanni’s diagram to show that angle ABC, the angle at which the Tower is leaning relative to the
horizontal, is 85° to the nearest degree. -
17M.1.SL.TZ1.T_9a:
Find the radius, , of the circular base of the cone.
-
17M.2.SL.TZ1.T_2b:
Find the length of CD.
-
17M.2.SL.TZ1.T_2c:
Show that angle , correct to one decimal place.
-
17M.2.SL.TZ2.S_4b:
Find the value of .
-
16N.2.AHL.TZ0.H_9b:
Show that .
-
16N.2.AHL.TZ0.H_9c:
Hence find the value of given that the shaded area is equal to 4.
-
17N.2.SL.TZ0.S_10b.ii:
Find the equation of .
-
17M.2.SL.TZ1.T_4a:
Calculate the volume of this pan.
-
17M.2.SL.TZ1.T_4e:
Calculate, to the nearest second, the time since the pizza was taken out of the oven until it can be eaten.
-
17M.2.SL.TZ1.T_4f:
In the context of this model, state what the value of 19 represents.
-
16N.1.SL.TZ0.T_7a:
Calculate the volume of the balloon.
-
17N.2.SL.TZ0.T_3b:
Calculate angle .
-
17N.2.SL.TZ0.T_3d.i:
Calculate Abdallah’s estimate for the area.
-
18M.2.AHL.TZ1.H_11b.i:
Show that submarine B travels in the same direction as originally planned.
-
18M.1.AHL.TZ1.H_10d:
Show that P is the midpoint of AD.
-
17N.1.AHL.TZ0.H_9b.i:
Find an expression for in terms of a, b and ;
-
19M.2.AHL.TZ2.H_11a:
Find the Cartesian equation of the plane containing P, Q and R.
-
19M.2.AHL.TZ2.H_11d.ii:
Given that П3 is equally inclined to both П1 and П2, determine two distinct possible Cartesian equations for П3.
-
18M.1.SL.TZ1.S_9a:
Show that
-
16N.1.SL.TZ0.S_4a:
Find a vector equation of the line that passes through P and Q.
-
16N.1.SL.TZ0.S_4b:
The line through P and Q is perpendicular to the vector 2i nk. Find the value of .
-
19N.1.AHL.TZ0.H_11c.i:
At , find the value of and the value of .
-
19N.1.AHL.TZ0.H_4:
and are acute angles such that and .
Show that .
-
19N.1.SL.TZ0.S_9a.i:
.
-
19N.2.SL.TZ0.S_4a:
Find .
-
17N.1.SL.TZ0.S_9a.i:
Show that .
-
16N.1.AHL.TZ0.H_13b:
Show that where .
-
19M.2.AHL.TZ2.H_3c:
Find the probability that Iqbal passes his third paper, given that he passed only one previous paper.
-
17M.1.SL.TZ2.S_9d:
Hence or otherwise, find the distance between and two seconds after they leave A.
-
17M.1.SL.TZ2.T_3b:
Find the total length of wire needed to construct this wireframe. Give your answer in centimetres correct to the nearest millimetre.
-
19M.1.SL.TZ2.T_9a:
Find the angle of elevation from B to C.
-
18M.1.SL.TZ1.S_6:
Six equilateral triangles, each with side length 3 cm, are arranged to form a hexagon.
This is shown in the following diagram.The vectors p , q and r are shown on the diagram.
Find p•(p + q + r).
-
17M.1.SL.TZ2.S_9b.i:
Find ;
-
18M.1.SL.TZ1.T_8a:
On the diagram, draw and label with an x the angle of depression of B from P.
-
20N.2.AHL.TZ0.H_10c:
Find the equation of , giving your answer in the form .
-
20N.2.AHL.TZ0.H_11c:
Find the maximum displacement of , in metres, from its initial position.
-
20N.2.SL.TZ0.S_8a.iii:
Hence find the number of rotations the water wheel makes in one hour.
-
20N.1.SL.TZ0.T_1b:
Calculate James’s estimate of its volume, in .
-
20N.1.SL.TZ0.T_1c:
The actual volume of the asteroid is found to be .
Find the percentage error in James’s estimate of the volume.
-
20N.2.SL.TZ0.T_3a:
Calculate the length of .
-
EXN.2.AHL.TZ0.11a:
Find the vectors and .
-
21M.1.SL.TZ1.2a:
Write down the radius of the planet.
-
21M.1.SL.TZ1.6b:
Hence or otherwise, solve for .
-
21M.1.AHL.TZ2.5:
Given any two non-zero vectors, and , show that .
-
21M.1.SL.TZ2.1a:
Find the value of .
-
21M.1.SL.TZ2.1b:
Hence, find the exact area of the non-shaded region.
-
21M.1.AHL.TZ2.8a:
Show that and do not intersect.
-
21M.1.SL.TZ2.6:
The following diagram shows triangle , with , and .
Given that , find the area of the triangle.
Give your answer in the form where .
-
21M.1.AHL.TZ2.12c:
Verify that for .
-
21M.2.AHL.TZ2.12b:
By considering limits, show that the graph of has a horizontal asymptote and state its equation.
-
21M.2.AHL.TZ2.12c.ii:
By using the expression for and the result , show that is decreasing for .
-
21N.1.SL.TZ0.6a:
Show that .
-
21N.2.SL.TZ0.5a:
Given that the areas of the two shaded regions are equal, show that .
-
22M.1.SL.TZ1.9a.ii:
By using a suitable substitution for , show that .
-
22M.2.SL.TZ1.7a:
Find .
-
22M.1.AHL.TZ1.11c:
Find the distance between and .
-
22M.1.AHL.TZ1.11b.ii:
Find a vector equation of , the line of intersection of and .
-
22M.2.SL.TZ2.8b:
Find the values of when .
-
22M.2.AHL.TZ2.7b:
Using l’Hôpital’s rule, show algebraically that the value of the limit is .
-
SPM.2.SL.TZ0.1a:
Find the volume of the sphere expressing your answer in the form , and .
-
SPM.2.SL.TZ0.9a:
Find the period of .
-
SPM.2.SL.TZ0.7b.i:
Show that is 101°.
-
SPM.2.SL.TZ0.2a:
Find the value of θ, giving your answer in radians.
-
EXM.3.AHL.TZ0.5a.i:
Sketch the graph , for
-
16N.2.AHL.TZ0.H_5c:
Solve the inequality .
-
16N.1.SL.TZ0.S_2b:
Find .
-
18N.1.SL.TZ0.S_7:
Given that , where , find the value of .
-
19M.1.AHL.TZ1.H_9c:
Hence or otherwise find in the form where , .
-
19M.2.AHL.TZ1.H_10a:
Write down the maximum and minimum value of .
-
19M.2.AHL.TZ1.H_10f:
With reference to your graph of explain why > 0 for all > 0.
-
18M.2.AHL.TZ2.H_4a.ii:
Find in radians.
-
19M.2.SL.TZ2.T_2d:
The length of path AD is 287 m.
Find the area of the region ABCD.
-
16N.2.SL.TZ0.T_5f:
the length of the fence, BP.
-
19M.2.SL.TZ1.S_8d:
The equation has two solutions where ≤ ≤ . Find both solutions.
-
19M.1.SL.TZ1.T_15b:
Find .
-
16N.2.SL.TZ0.T_6d:
Show that .
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
18M.2.SL.TZ1.T_1d:
Calculate the length of AE.
-
18M.2.SL.TZ2.T_5a.iii:
Use Giovanni's diagram to find the length of BX, the horizontal displacement of the Tower.
-
18M.2.SL.TZ2.T_5b:
Find the percentage error on Giovanni’s diagram.
-
18M.1.SL.TZ2.T_15b:
The total external surface area of the pencil case rounded to 3 significant figures is 570 cm2.
Using your graphic display calculator, calculate the value of r.
-
19M.1.SL.TZ2.S_9a:
Find the value of .
-
17M.2.SL.TZ1.T_2a.ii:
Show that the equation in part (a)(i) simplifies to .
-
17M.2.SL.TZ1.T_2d:
Find the length of the perimeter of ABCDE.
-
17N.2.SL.TZ0.S_10d:
A saw has a toothed edge which is 300 mm long. Find the number of complete teeth on this saw.
-
17M.1.SL.TZ1.S_8b:
A second line , has equation r = .
Given that and are perpendicular, show that .
-
17M.1.SL.TZ1.S_8c:
The lines and intersect at . Find .
-
17M.1.SL.TZ1.S_8d.ii:
Hence or otherwise, find one point on which is units from C.
-
19M.1.SL.TZ1.T_15a:
Write down an equation for the area, , of the curved surface in terms of .
-
19M.1.SL.TZ2.S_2b:
perpendicular.
-
18M.1.AHL.TZ2.H_1:
The acute angle between the vectors 3i − 4j − 5k and 5i − 4j + 3k is denoted by θ.
Find cos θ.
-
18M.2.SL.TZ1.S_10b.i:
For the graph of , write down the amplitude.
-
18M.2.SL.TZ1.S_10d:
Find the maximum speed of the ball.
-
17N.2.SL.TZ0.T_3d.ii:
Find the percentage error in Abdallah’s estimate.
-
18M.2.AHL.TZ1.H_11b.ii:
Find the value of t when submarine B passes through P.
-
18M.2.AHL.TZ1.H_11c.i:
Find an expression for the distance between the two submarines in terms of t.
-
17N.1.AHL.TZ0.H_9d:
Deduce an expression for in terms of a and b only.
-
19M.2.AHL.TZ2.H_11c:
Given that П3 is parallel to the line , show that .
-
18N.1.AHL.TZ0.H_9a:
Find, in terms of , a Cartesian equation of the plane Π containing this triangle.
-
18M.1.SL.TZ1.S_9b.ii:
Point C (k , 12 , −k) is on L. Show that k = 14.
-
18M.1.SL.TZ1.S_9c.ii:
Write down the value of angle OBA.
-
18M.1.AHL.TZ2.H_9a.ii:
Using vector algebra, show that .
-
18M.1.AHL.TZ2.H_9d:
Find the vector equation of the straight line passing through M and normal to the plane containing ABCD.
-
18M.1.AHL.TZ2.H_9f.i:
Find the coordinates of X, Y and Z.
-
18M.1.SL.TZ2.S_1b:
The vector is perpendicular to . Find the value of p.
-
17M.2.AHL.TZ2.H_9a:
Find the vector equation of the line (BC).
-
19N.2.SL.TZ0.S_2a:
Find the point of intersection of and .
-
17N.1.SL.TZ0.S_9a.ii:
Find a vector equation for .
-
17N.1.SL.TZ0.S_9c:
The point D has coordinates . Given that is perpendicular to , find the possible values of .
-
SPM.3.AHL.TZ0.2a:
On the same set of axes, sketch the graphs of and for −1 ≤ ≤ 1.
-
SPM.3.AHL.TZ0.2g:
Use an appropriate trigonometric identity to show that .
-
16N.1.AHL.TZ0.H_13c:
Use the principle of mathematical induction to prove that
where .
-
18N.2.SL.TZ0.T_5d:
A vertical pole, TB, is constructed at point B and has height 25 m.
Calculate the angle of elevation of T from, M, the midpoint of the side AC.
-
17M.2.AHL.TZ2.H_4a:
Find the set of values of that satisfy the inequality .
-
16N.1.SL.TZ0.T_11a:
Calculate CD, the height of the observation deck above the ground.
-
19M.2.SL.TZ1.S_9a:
Find the gradient of .
-
20N.2.AHL.TZ0.H_10b:
Find the shortest distance from the point to .
-
20N.1.SL.TZ0.S_9a:
Express in terms of .
-
20N.1.SL.TZ0.S_9b:
Find the value of .
-
20N.1.SL.TZ0.S_9c:
Consider a unit vector , such that , where .
Point is such that .
Find the coordinates of .
-
20N.2.SL.TZ0.S_8a.i:
Find the height of point above the ground.
-
20N.2.SL.TZ0.S_8b:
Find .
-
21M.2.SL.TZ1.8e.ii:
Find the length of new fence required.
-
EXN.1.SL.TZ0.9a:
Find the height of the ball above the ground when it is released.
-
EXN.1.AHL.TZ0.8b.i:
the value of .
-
21M.2.SL.TZ1.8c:
The area of field that the horse can reach is . Find the value of .
-
21M.2.AHL.TZ1.6a:
Find a Cartesian equation of the plane which is perpendicular to and and passes through the origin .
-
21M.2.SL.TZ1.8b:
Show that the area of the field that the horse can reach is .
-
21M.2.SL.TZ2.7b:
Find the angle of elevation of point from point .
-
19M.1.SL.TZ1.S_3b:
Find the value of .
-
21N.1.SL.TZ0.6b:
Hence or otherwise, solve the equation for .
-
21N.2.SL.TZ0.8b:
Find the value of .
-
21N.2.SL.TZ0.8e:
Find the height of the water at .
-
21N.2.AHL.TZ0.11a.i:
Find the vector and the vector .
-
21N.2.AHL.TZ0.11c.ii:
Hence find the coordinates of .
-
21N.2.AHL.TZ0.11d.ii:
Hence find the vector equation of the line formed when is reflected in the plane .
-
22M.1.SL.TZ2.5:
Find the least positive value of for which .
-
22M.1.AHL.TZ2.7:
By using the substitution or otherwise, find an expression for in terms of , where is a non-zero real number.
-
22M.2.AHL.TZ2.11a:
Find the three-figure bearing on which airplane is travelling.
-
SPM.1.SL.TZ0.6b:
Hence or otherwise solve for .
-
SPM.2.AHL.TZ0.12b:
Verify that and satisfy the equation .
-
SPM.2.SL.TZ0.9d:
Find the value of for which the functions have the greatest difference.
-
SPM.2.AHL.TZ0.12d:
Using the results from parts (b) and (c) find the exact value of .
Give your answer in the form where , .
-
EXM.3.AHL.TZ0.5a.iii:
Write down the period of this graph
-
EXM.3.AHL.TZ0.5e.iv:
.
-
18M.1.SL.TZ1.T_8c:
Find the size of the angle of depression of B from P.
-
18N.1.AHL.TZ0.H_11a:
Find the roots of which satisfy the condition , expressing your answers in the form , where , .
-
18N.1.AHL.TZ0.H_11b.i:
Show that Re S = Im S.
-
18M.1.AHL.TZ1.H_8:
Let .
Find, in terms of b, the solutions of .
-
18N.2.SL.TZ0.S_7b:
Hence or otherwise, find the total distance along the road where the signal from the tower can reach cellular phones.
-
16N.2.SL.TZ0.T_5b:
the size of angle DAB;
-
16N.2.SL.TZ0.T_5e:
the length of AP;
-
17M.1.SL.TZ1.S_3:
The following diagram shows triangle PQR.

Find PR.
-
17N.2.AHL.TZ0.H_11a.ii:
Sketch a graph of for .
-
17N.2.AHL.TZ0.H_11b.i:
Express in terms of .
-
17N.1.SL.TZ0.S_4b:
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

Find the exact perimeter of this shape.
-
18M.1.SL.TZ2.T_8b:
Calculate the area of the park.
-
17M.2.AHL.TZ1.H_8b:
Calculate when .
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
17N.2.SL.TZ0.T_6e:
Find the total cost of the ingredients of one special dessert.
-
19M.2.SL.TZ1.T_2a:
Find the length , giving your answer to four significant figures.
-
19M.2.SL.TZ2.T_3c:
Show that the total surface area of the cone-shaped container is 314 cm2, correct to three significant figures.
-
19M.2.SL.TZ2.T_3e:
The factory director wants to increase the volume of coconut water sold per container.
State whether or not they should replace the cone-shaped containers with cylinder‑shaped containers. Justify your conclusion.
-
18N.1.SL.TZ0.T_9b:
1 cm3 of glass has a mass of 2.56 grams.
Calculate the mass, in grams, of the paperweight.
-
17M.2.SL.TZ1.T_2a.i:
Write down an equation for the area of ABCDE using the above information.
-
17M.2.SL.TZ2.S_4a:
Find the value of .
-
17M.2.SL.TZ2.T_4d:
Find the length of the path CE.
-
17N.2.SL.TZ0.S_10b.i:
Find the coordinates of and of .
-
19M.1.AHL.TZ1.H_1:
Let a = and b = , .
Given that a and b are perpendicular, find the possible values of .
-
19M.1.AHL.TZ2.H_2a.i:
Find the vector .
-
17N.2.SL.TZ0.S_3b:
Let . Find .
-
16N.1.AHL.TZ0.H_4a:
Find a b.
-
16N.1.AHL.TZ0.H_4b:
Hence find the Cartesian equation of the plane containing the vectors a and b, and passing through the point .
-
17M.1.SL.TZ1.T_13b:
Find the area of the postage stamp.
-
19M.1.AHL.TZ1.H_11d:
Write down and .
-
17N.1.AHL.TZ0.H_9a.i:
Find, in terms of a and b .
-
17N.1.AHL.TZ0.H_9c:
Show that , and find the value of .
-
19M.2.AHL.TZ2.H_11d.i:
Show that .
-
18M.1.AHL.TZ2.H_9b:
Show that p = 1, q = 1 and r = 4.
-
18M.1.AHL.TZ2.H_9f.ii:
Find YZ.
-
17M.1.AHL.TZ1.H_5a:
Find the area of the parallelogram ABCD.
-
18M.1.SL.TZ2.S_1a:
Find a vector equation for L1.
-
17M.2.AHL.TZ2.H_9f:
Find a vector perpendicular to the plane Π.
-
16N.1.AHL.TZ0.H_8b:
determine the coordinates of the point of intersection P.
-
19N.1.AHL.TZ0.H_11a.ii:
Hence, show that, if the angle between the faces and is , then .
-
19N.1.AHL.TZ0.H_9c.i:
By considering triangle , show that .
-
19N.2.AHL.TZ0.H_4b:
the area.
-
19N.1.SL.TZ0.S_9b:
Given that , show that .
-
19N.2.SL.TZ0.S_2c:
passes through the intersection of and .
Write down a vector equation for .
-
SPM.2.AHL.TZ0.7:
Two ships, A and B , are observed from an origin O. Relative to O, their position vectors at time t hours after midday are given by
rA =
rB =
where distances are measured in kilometres.
Find the minimum distance between the two ships.
-
SPM.3.AHL.TZ0.2c:
On a new set of axes, sketch the graphs of and for −1 ≤ ≤ 1.
-
19M.1.SL.TZ1.S_2a:
Find .
-
18N.1.AHL.TZ0.H_10d:
Find the area enclosed by the curve and the -axis between B and D, as shaded on the diagram.
-
17M.1.SL.TZ2.S_2a:
Find the value of .
-
18N.2.SL.TZ0.S_8b.i:
Find the value of .
-
19M.1.SL.TZ2.S_7b:
Consider the graph of , 0 ≤ < , where > 0.
Find the greatest value of such that the graph of does not intersect the line .
-
18M.2.SL.TZ2.S_8c:
Find the area of triangle PQR.
-
16N.2.SL.TZ0.S_3c:
Find AB.
-
17M.1.SL.TZ1.S_10a:
Show that .
-
18N.2.SL.TZ0.T_5b:
Calculate the area of triangle ABC.
-
18N.2.SL.TZ0.T_5c:
Find the length of AC.
-
18N.2.SL.TZ0.T_5a:
Show that the size of angle BÂC is 20.2°, correct to 3 significant figures.
-
16N.2.AHL.TZ0.H_7b:
Find the difference between the areas of the two possible triangles ABC.
-
17M.2.SL.TZ1.S_8c:
There are two high tides on 12 December 2017. At what time does the second high tide occur?
-
17M.2.SL.TZ1.S_8b.i:
Find the value of ;
-
17N.2.AHL.TZ0.H_5:
Barry is at the top of a cliff, standing 80 m above sea level, and observes two yachts in the sea.
“Seaview” is at an angle of depression of 25°.
“Nauti Buoy” is at an angle of depression of 35°.
The following three dimensional diagram shows Barry and the two yachts at S and N.
X lies at the foot of the cliff and angle 70°.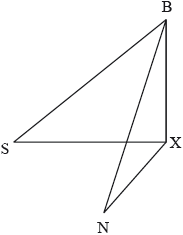
Find, to 3 significant figures, the distance between the two yachts.
-
17M.2.SL.TZ1.S_5:
The following diagram shows the chord [AB] in a circle of radius 8 cm, where .

Find the area of the shaded segment.
-
20N.2.AHL.TZ0.H_10d:
Determine the acute angle between and .
-
20N.2.AHL.TZ0.H_11e.i:
Show that, at these times, .
-
20N.2.AHL.TZ0.H_11e.ii:
Hence show that .
-
20N.1.SL.TZ0.S_2b:
Find .
-
20N.1.SL.TZ0.T_1a:
Write down the value of the iron in the form where .
-
20N.2.SL.TZ0.T_3c:
Calculate the area of triangle .
-
EXN.2.SL.TZ0.2b:
Show that .
-
EXN.2.AHL.TZ0.11b:
Use a vector method to show that .
-
EXN.2.AHL.TZ0.11c:
Show that the Cartesian equation of the plane that contains the triangle is .
-
EXN.2.AHL.TZ0.11d.i:
Find a vector equation of the line .
-
EXN.2.AHL.TZ0.11d.ii:
Hence determine the minimum distance, , from to .
-
EXN.2.AHL.TZ0.11e:
Find the volume of right-pyramid .
-
21M.2.SL.TZ2.7c:
Find the length of each blade of the windmill.
-
21M.2.AHL.TZ2.12e:
State the domain of .
-
21N.2.AHL.TZ0.9f:
Determine the number of hours, over a 24-hour period, for which the tide is higher than metres.
-
21N.2.AHL.TZ0.11c.i:
Show that at the point .
-
21N.2.AHL.TZ0.11d.i:
Find the reflection of the point in the plane .
-
22M.2.SL.TZ1.7d:
A second ornament is in the shape of a cuboid with a rectangular base of length , width and height . The cuboid has the same volume as the pyramid.
The cuboid has a minimum surface area of . Find the value of .
-
22M.2.SL.TZ2.7c:
Find .
-
22M.2.AHL.TZ2.11e:
Let represent the distance between airplane and airplane for .
Find the minimum value of .
-
22M.1.SL.TZ1.9b.ii:
It is given that , where . Find the value of .
-
22M.1.AHL.TZ2.11c:
Given that , find the value of .
Give your answer in the form , where .
-
SPM.1.SL.TZ0.1a:
Given that find the value of .
-
SPM.2.SL.TZ0.2b:
Find the area of the shaded region.
-
SPM.2.SL.TZ0.7a:
Find the distance from point A to point B.
-
EXM.3.AHL.TZ0.5g:
Hence prove your conjectures in part (e).
-
EXM.3.AHL.TZ0.5f.ii:
Show that .
-
EXM.3.AHL.TZ0.5c.ii:
Comment on your answer to part (c)(i).
-
17M.1.SL.TZ1.S_8a.i:
Find .
-
16N.2.AHL.TZ0.H_5a:
Sketch the graph of indicating clearly any intercepts with the axes and the coordinates of any local maximum or minimum points.
-
19M.2.SL.TZ2.S_3a:
Find BD.
-
19M.2.AHL.TZ1.H_10c:
Sketch the graph of for 0 ≤ ≤ 0.02 , showing clearly the coordinates of the first maximum and the first minimum.
-
19M.2.SL.TZ2.T_2b.i:
Find the size of angle .
-
19M.2.SL.TZ2.T_2b.ii:
Find the size of angle .
-
19M.1.SL.TZ2.T_9b:
A second truck arrives whose ladder, when fully extended, is 30 metres long. The base of this ladder is also 4 metres above the ground. For safety reasons, the maximum angle of elevation that the ladder can make is 70º.
Find the maximum height on the wall that can be reached by the ladder on the second truck.
-
19M.2.SL.TZ2.S_4a:
Show that .
-
19M.2.SL.TZ2.S_4c:
Given that the area of triangle OBC is of the area of sector OAB, find θ.
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
17M.1.AHL.TZ2.H_11c.ii:
Hence find the cube roots of in modulus-argument form.
-
18M.1.SL.TZ2.T_15a:
Find an expression for the slant height of the cone in terms of r.
-
19M.2.SL.TZ2.T_3d:
Find the height, , of this cylinder-shaped container.
-
17M.2.SL.TZ1.T_2e:
Calculate the length of CF.
-
17M.2.SL.TZ2.S_1c:
Find the area of sector OABC.
-
17M.2.SL.TZ2.S_4c:
Use the model to find the depth of the water 10 hours after high tide.
-
17M.2.SL.TZ2.T_4e:
Calculate the total length of the track.
-
16N.2.AHL.TZ0.H_9a:
Find an expression for the shaded area in terms of , and .
-
17M.1.SL.TZ1.S_8a.ii:
Hence, write down a vector equation for .
-
17M.2.SL.TZ1.T_4d:
Find the temperature that the pizza will be 5 minutes after it is taken out of the oven.
-
18M.1.AHL.TZ1.H_10b:
Find the angle between the faces ABD and BCD.
-
18M.1.AHL.TZ1.H_10c:
Find the Cartesian equation of .
-
18N.1.AHL.TZ0.H_9c:
Show that L does not intersect the -axis for any negative value of .
-
18M.1.SL.TZ1.S_9c.i:
Find .
-
18M.1.AHL.TZ2.H_9a.i:
Explain why ABCD is a parallelogram.
-
17M.1.AHL.TZ1.H_5b:
By using a suitable scalar product of two vectors, determine whether is acute or obtuse.
-
17M.2.AHL.TZ2.H_9d:
Show that the line (BC) lies in the plane Π.
-
17M.2.AHL.TZ2.H_9g:
Find the acute angle between the planes Π and Π.
-
19N.1.AHL.TZ0.H_11b.ii:
Comment on the positions of in relation to the plane .
-
19N.1.AHL.TZ0.H_11c.ii:
Find the equation of the horizontal asymptote of the graph.
-
19N.2.AHL.TZ0.H_4a:
the perimeter.
-
19N.1.SL.TZ0.S_9a.ii:
.
-
19N.1.SL.TZ0.S_9c:
Calculate the area of triangle .
-
19N.2.SL.TZ0.S_10c:
During the second stage, the rocket accelerates at a constant rate. The distance which the rocket travels during the second stage is the same as the distance it travels during the first stage.
Find the total time taken for the two stages.
-
19N.2.SL.TZ0.S_2b:
Write down a direction vector for .
-
SPM.3.AHL.TZ0.2d.ii:
local minimum points.
-
SPM.3.AHL.TZ0.2f:
Use an appropriate trigonometric identity to show that .
-
SPM.3.AHL.TZ0.2d.i:
local maximum points;
-
SPM.3.AHL.TZ0.2b.ii:
local minimum points;
-
16N.1.AHL.TZ0.H_13a:
Find the value of .
-
19M.1.SL.TZ1.S_2b:
A second line, , is parallel to and passes through (1, 2, 3).
Write down a vector equation for .
-
16N.2.SL.TZ0.S_3b:
Find the value of .
-
17M.1.SL.TZ2.S_9b.ii:
Find .
-
18N.2.SL.TZ0.S_8d:
Find the area of triangle ABC.
-
17M.2.SL.TZ1.S_8b.ii:
Find the value of ;
-
18N.2.SL.TZ0.S_8a.i:
Find .
-
18N.1.AHL.TZ0.H_3a:
For , sketch the graph of . Indicate clearly the maximum and minimum values of the function.
-
18N.2.AHL.TZ0.H_7:
Boat A is situated 10km away from boat B, and each boat has a marine radio transmitter on board. The range of the transmitter on boat A is 7km, and the range of the transmitter on boat B is 5km. The region in which both transmitters can be detected is represented by the shaded region in the following diagram. Find the area of this region.
-
20N.1.SL.TZ0.S_2a:
Given that is acute, find .
-
21M.1.SL.TZ1.2b:
The volume of the planet can be expressed in the form where and .
Find the value of and the value of .
-
21M.1.AHL.TZ1.12a:
Show that .
-
21M.1.AHL.TZ1.11c:
It is given that the lines and have a unique point of intersection, , when .
Find the value of , and find the coordinates of the point in terms of .
-
21M.2.AHL.TZ1.9a:
Show that .
-
21M.1.SL.TZ2.8d:
Hence, find the volume of the cone.
-
21M.1.AHL.TZ2.2:
Solve the equation .
-
21M.3.AHL.TZ1.2d:
Use the results from parts (b) and (c) to show that .
-
21N.2.SL.TZ0.5b:
Hence determine the value of .
-
21N.2.SL.TZ0.8d:
Find the smallest possible value of .
-
21N.2.AHL.TZ0.9d:
Find the smallest possible value of .
-
21M.1.AHL.TZ1.6:
It is given that , where . Find the exact value of .
-
22M.1.SL.TZ1.4b:
Solve the equation where .
-
22M.1.SL.TZ1.9b.i:
Show that , where is a positive real constant.
-
22M.1.AHL.TZ1.11a:
Show that the three planes do not intersect.
-
SPM.2.SL.TZ0.1b:
The sphere is to be melted down and remoulded into the shape of a cone with a height of 14.8 cm.
Find the radius of the base of the cone, correct to 2 significant figures.
-
SPM.2.SL.TZ0.7e:
Jacob hikes at an average speed of 3.9 km/h.
Find, to the nearest minute, the time it takes for Jacob to reach point C.
-
EXM.3.AHL.TZ0.5c.i:
Find , giving the answer to 3 significant figures.
-
16N.1.SL.TZ0.S_2a:
Find .
-
19M.2.SL.TZ2.S_3b:
The area of triangle ABD is 18.5 cm2. Find the possible values of θ.
-
18M.1.SL.TZ1.T_14b:
Calculate the curved surface area of the cone which has been removed.
-
19M.1.AHL.TZ2.H_9c:
At the points A and B on the diagram, the gradients of the two graphs are equal.
Determine the -coordinate of A on the graph of .
-
19M.2.AHL.TZ1.H_10g:
Given that can be written as where , , , > 0, use your graph to find the values of , , and .
-
18M.2.AHL.TZ2.H_4a.i:
Find AM.
-
18M.2.SL.TZ1.S_3b:
The area of the shaded region is 12 cm2. Find the value of θ.
-
19M.2.SL.TZ2.T_2c:
Find the size of angle .
-
18N.2.SL.TZ0.S_7a:
Let SR = . Use the cosine rule to show that .
-
19M.1.AHL.TZ1.H_3:
A sector of a circle with radius cm , where > 0, is shown on the following diagram.
The sector has an angle of 1 radian at the centre.Let the area of the sector be cm2 and the perimeter be cm. Given that , find the value of .
-
17N.2.AHL.TZ0.H_11a.iii:
Find the -coordinate(s) of the point(s) of inflexion of the graph of , labelling these clearly on the graph of .
-
19M.2.SL.TZ1.S_8a:
The range of is ≤ ≤ . Find and .
-
18M.1.SL.TZ2.T_8a:
Calculate the length of side AC in km.
-
19M.1.SL.TZ1.T_15c:
Find the value of when the area of the curved surface is maximized.
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
17N.2.SL.TZ0.T_6c:
Find the cost of of chocolate mousse.
-
17N.2.SL.TZ0.T_6f:
Find the value of .
-
17M.1.AHL.TZ2.H_11b:
Show that .
-
18M.2.SL.TZ1.T_1a:
Calculate the area of triangle EAD.
-
19M.2.SL.TZ1.T_2b:
Find the total area of the two rectangles that make up the roof.
-
19M.2.SL.TZ1.T_2c:
Find the maximum number of complete panels that can be fitted to the whole roof.
-
17M.2.SL.TZ2.S_1b:
Find the perimeter of sector OABC.
-
17M.2.SL.TZ2.T_4a:
Find the length of the path BD.
-
18M.2.SL.TZ1.S_10e:
Find the first time when the ball’s speed is changing at a rate of 2 cm s−2.
-
17M.2.SL.TZ1.T_4b:
Find the radius of the sphere in cm, correct to one decimal place.
-
17N.2.SL.TZ0.T_3c:
Find the area of ABCD.
-
18M.2.AHL.TZ1.H_11a:
Show that the two submarines would collide at a point P and write down the coordinates of P.
-
19M.1.AHL.TZ1.H_11b:
Verify that is the point of intersection of the two lines.
-
17N.1.AHL.TZ0.H_9e:
Given that area , find the value of .
-
19M.2.AHL.TZ2.H_11b:
Given that П1 and П2 meet in a line , verify that the vector equation of can be given by r .
-
18M.1.SL.TZ1.S_9d:
Point D is also on L and has coordinates (8, 4, −9).
Find the area of triangle OCD.
-
18N.1.AHL.TZ0.H_5a:
Find and simplify an expression for a • b in terms of .
-
19N.1.AHL.TZ0.H_11b.i:
Find the two possible coordinates of .
-
19N.1.AHL.TZ0.H_9c.ii:
By considering triangle , find another expression for in terms of and .
-
19N.1.SL.TZ0.S_6:
Let , for . Find the values of for which .
-
18N.1.AHL.TZ0.H_10b:
Hence, show that , .
-
18N.1.SL.TZ0.S_5:
Consider the vectors a = and b = .
Find the possible values of p for which a and b are parallel.
-
17M.1.SL.TZ2.S_2b:
Given that c = a + 2b, find c.
-
19M.2.AHL.TZ2.H_3b:
Calculate the probability that Iqbal passes at least two of the papers he attempts.
-
17M.1.SL.TZ2.S_9a:
Find the coordinates of A.
-
16N.2.AHL.TZ0.H_7a:
Use the cosine rule to find the two possible values for AC.
-
18M.2.SL.TZ2.S_8d:
Hence or otherwise find the shortest distance from R to the line through P and Q.
-
19M.1.SL.TZ1.T_8a:
Draw and label the angle of depression on the diagram.
-
18N.1.AHL.TZ0.H_3c.ii:
For the value of found in part (b), find an expression for .
-
17M.2.SL.TZ1.S_8a.ii:
Find the difference in height between low tide and high tide.
-
17M.1.AHL.TZ1.H_3:
Solve the equation .
-
16N.2.SL.TZ0.S_3a:
Write down the exact value of in radians.
-
18N.1.AHL.TZ0.H_3c.i:
For the value of found in part (b), write down the domain of .
-
20N.2.AHL.TZ0.H_11a:
Find the times when comes to instantaneous rest.
-
20N.2.SL.TZ0.S_7a:
Show that .
-
20N.2.SL.TZ0.S_8d:
Determine the rate of change of when the top of the bucket is at .
-
20N.2.SL.TZ0.T_3d:
Pedro draws a circle, with centre at point , passing through point . Part of the circle is shown in the diagram.
Show that point lies outside this circle. Justify your reasoning.
-
EXN.1.AHL.TZ0.7:
Consider quadrilateral where is parallel to .
In , , , and .
Find an expression for in terms of and .
-
EXN.1.SL.TZ0.9c:
Show that the ball takes seconds to return to its initial height above the ground for the first time.
-
21M.1.AHL.TZ1.11a.ii:
Find a vector equation of .
-
21M.1.AHL.TZ1.11b:
Find the possible values of when the acute angle between and is .
-
21M.2.SL.TZ1.8a:
Write down an expression for in terms of .
-
21M.1.AHL.TZ2.8b:
Find the minimum distance between and .
-
21M.1.SL.TZ2.8a:
Find the -coordinates of and .
-
21M.2.AHL.TZ2.12d:
Find an expression for , justifying your answer.
-
21N.2.SL.TZ0.3:
Consider a triangle , where and .
Find the smallest possible perimeter of triangle .
-
21N.2.SL.TZ0.8c:
Find the value of .
-
21N.2.SL.TZ0.8f:
Determine the number of hours, over a 24-hour period, for which the tide is higher than metres.
-
21N.2.AHL.TZ0.9g:
A fisherman notes that the water height at nearby Folkestone harbour follows the same sinusoidal pattern as that of Dungeness harbour, with the exception that high tides (and low tides) occur minutes earlier than at Dungeness.
Find a suitable equation that may be used to model the tidal height of water at Folkestone harbour.
-
22M.1.SL.TZ1.6b:
The -intercept of the graph of is at .
Given that , find the smallest value of .
-
22M.2.SL.TZ1.7b:
Given that , find .
-
22M.2.AHL.TZ1.7a:
Find the possible range of values for .
-
22M.2.AHL.TZ1.7c:
Find such that and is perpendicular to .
-
22M.2.SL.TZ2.7b:
Find the area of this piece of land.
-
22M.2.AHL.TZ2.11b:
Show that airplane travels at a greater speed than airplane .
-
22M.1.AHL.TZ1.9b:
Hence, given that , find the value of .
-
22M.1.AHL.TZ1.11b.i:
Verify that the point lies on both and .
-
SPM.2.AHL.TZ0.12a:
Show that .
-
SPM.1.SL.TZ0.6a:
Show that .
-
SPM.2.SL.TZ0.7c:
Find .
-
EXM.3.AHL.TZ0.5e.i:
.
-
16N.2.AHL.TZ0.H_5b:
State the range of .
-
18M.1.SL.TZ1.T_8b:
Find the size of angle APB.
-
19M.1.AHL.TZ1.H_9b:
Show that .
-
18M.1.SL.TZ1.T_14a:
Calculate the radius of the base of the cone which has been removed.
-
19M.1.AHL.TZ2.H_9b:
Find the exact area of the shaded region, giving your answer in the form , where , .
-
16N.2.SL.TZ0.T_5c:
the area of triangle ABD;
-
16N.2.SL.TZ0.T_5d:
the area of quadrilateral ABCD;
-
17N.2.AHL.TZ0.H_11c:
Solve the equation , giving your answers in the form where .
-
19M.2.SL.TZ1.S_8b:
Find the range of .
-
19M.2.SL.TZ1.S_8c.ii:
Find the period of .
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
17M.1.AHL.TZ2.H_11c.i:
Find the modulus and argument of in terms of . Express each answer in its simplest form.
-
18M.2.SL.TZ1.T_1b:
Calculate the total volume of the barn.
-
18M.2.SL.TZ1.T_1e:
Show that Farmer Brown is incorrect.
-
18M.2.SL.TZ1.T_1f:
Calculate the total length of metal required for one support.
-
17M.1.SL.TZ2.T_12b:
Find the value of .
-
19M.2.SL.TZ1.T_2d:
Find the percentage error in her estimate.
-
18N.1.SL.TZ0.T_9a.i:
Write down the value of x.
-
17M.1.SL.TZ1.T_9c:
Find the curved surface area of the cone.
-
16N.2.SL.TZ0.S_10c:
(i) Find .
(ii) Hence or otherwise, find the maximum positive rate of change of .
-
17N.2.AHL.TZ0.H_3:
This diagram shows a metallic pendant made out of four equal sectors of a larger circle of radius and four equal sectors of a smaller circle of radius .
The angle 20°.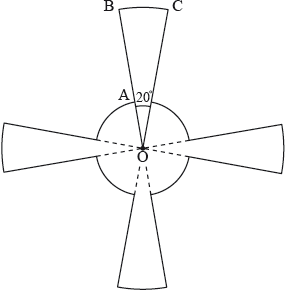
Find the area of the pendant.
-
19M.1.AHL.TZ2.H_2a.ii:
Find the vector .
-
19M.1.AHL.TZ2.H_2b:
Hence or otherwise, find the area of the triangle ABC.
-
18M.2.SL.TZ1.S_10a:
Find the coordinates of A.
-
18N.1.SL.TZ0.T_1a:
Calculate the volume of this hemisphere in cm3.
Give your answer correct to one decimal place.
-
17M.2.SL.TZ1.T_4c:
Find the value of .
-
17N.2.SL.TZ0.T_3a:
Show that correct to the nearest metre.
-
18M.2.AHL.TZ1.H_11c.ii:
Find the value of t when the two submarines are closest together.
-
18M.1.SL.TZ1.S_9b.i:
Find a vector equation for L.
-
18M.1.AHL.TZ2.H_9c:
Find the area of the parallelogram ABCD.
-
18M.1.AHL.TZ2.H_9e:
Find the Cartesian equation of .
-
17M.2.AHL.TZ1.H_7:
Find the Cartesian equation of plane Π containing the points and and perpendicular to the plane .
-
18N.1.AHL.TZ0.H_5b:
Hence or otherwise, find the values of for which the angle between a and b is obtuse .
-
17M.2.AHL.TZ2.H_9b:
Determine whether or not the lines (OA) and (BC) intersect.
-
17M.2.AHL.TZ2.H_9c:
Find the Cartesian equation of the plane Π, which passes through C and is perpendicular to .
-
19N.1.AHL.TZ0.H_11a.i:
Show that and find a similar expression for .
-
19N.1.AHL.TZ0.H_9a:
Given that , show that .
-
19N.1.AHL.TZ0.H_9d:
Use your answers to part (c) to show that .
-
19N.2.SL.TZ0.S_10a:
Find an expression for the velocity, m s−1, of the rocket during the first stage.
-
19N.2.SL.TZ0.S_10b:
Find the distance that the rocket travels during the first stage.
-
19N.2.SL.TZ0.S_4b:
Find the area of .
-
18N.1.AHL.TZ0.H_10c:
Find the -coordinates of A and of C , giving your answers in the form , where , .
-
SPM.1.AHL.TZ0.8:
The plane П has the Cartesian equation
The line L has the vector equation r . The acute angle between the line L and the plane П is 30°.
Find the possible values of .
-
16N.1.AHL.TZ0.H_13d:
Hence or otherwise solve the equation in the interval .
-
18M.2.SL.TZ1.S_6:
Triangle ABC has a = 8.1 cm, b = 12.3 cm and area 15 cm2. Find the largest possible perimeter of triangle ABC.
-
17M.1.SL.TZ2.S_9c:
Find .
-
16N.1.SL.TZ0.T_11b:
Calculate the angle of depression from A to B.
-
18N.2.SL.TZ0.S_8b.ii:
Show that .
-
17M.2.SL.TZ1.S_8a.i:
How much time is there between the first low tide and the next high tide?
-
19M.1.SL.TZ1.S_6:
The magnitudes of two vectors, u and v, are 4 and respectively. The angle between u and v is .
Let w = u − v. Find the magnitude of w.
-
17N.1.SL.TZ0.T_10b:
Write down the angle of elevation of B from E.
-
17M.1.SL.TZ2.T_3a:
Find the length of one of the straight pieces in the wireframe.
-
17N.2.SL.TZ0.S_1a:
Find BC.
-
16N.2.AHL.TZ0.H_2:
Find the acute angle between the planes with equations and .
Sub sections and their related questions
SL 3.1—3d space, volume, angles, distance, midpoints
-
SPM.2.SL.TZ0.1a:
Find the volume of the sphere expressing your answer in the form , and .
-
SPM.2.SL.TZ0.1b:
The sphere is to be melted down and remoulded into the shape of a cone with a height of 14.8 cm.
Find the radius of the base of the cone, correct to 2 significant figures.
-
19M.2.SL.TZ1.T_2a:
Find the length , giving your answer to four significant figures.
-
19M.2.SL.TZ1.T_2b:
Find the total area of the two rectangles that make up the roof.
-
19M.2.SL.TZ1.T_2c:
Find the maximum number of complete panels that can be fitted to the whole roof.
-
19M.2.SL.TZ1.T_2d:
Find the percentage error in her estimate.
-
19M.2.SL.TZ1.T_2e:
Olivia investigates arranging the panels, such that the longer edge of each panel is parallel to or .
State whether this new arrangement will allow Olivia to fit more solar panels to the roof. Justify your answer. -
18N.1.SL.TZ0.T_1a:
Calculate the volume of this hemisphere in cm3.
Give your answer correct to one decimal place.
-
18N.1.SL.TZ0.T_1b:
Write down your answer to part (a) correct to the nearest integer.
-
18N.1.SL.TZ0.T_1c:
Write down your answer to part (b) in the form a × 10k , where 1 ≤ a < 10 and k ∈ .
-
18M.1.SL.TZ1.T_14a:
Calculate the radius of the base of the cone which has been removed.
-
18M.1.SL.TZ1.T_14b:
Calculate the curved surface area of the cone which has been removed.
-
18M.1.SL.TZ1.T_14c:
Calculate the curved surface area of the remaining solid.
-
17M.2.SL.TZ1.T_4a:
Calculate the volume of this pan.
-
17M.2.SL.TZ1.T_4b:
Find the radius of the sphere in cm, correct to one decimal place.
-
17M.2.SL.TZ1.T_4c:
Find the value of .
-
17M.2.SL.TZ1.T_4d:
Find the temperature that the pizza will be 5 minutes after it is taken out of the oven.
-
17M.2.SL.TZ1.T_4e:
Calculate, to the nearest second, the time since the pizza was taken out of the oven until it can be eaten.
-
17M.2.SL.TZ1.T_4f:
In the context of this model, state what the value of 19 represents.
-
18M.1.SL.TZ2.T_15a:
Find an expression for the slant height of the cone in terms of r.
-
18M.1.SL.TZ2.T_15b:
The total external surface area of the pencil case rounded to 3 significant figures is 570 cm2.
Using your graphic display calculator, calculate the value of r.
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
16N.2.SL.TZ0.T_6d:
Show that .
-
16N.2.SL.TZ0.T_6e:
Find .
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
17M.1.SL.TZ1.T_9a:
Find the radius, , of the circular base of the cone.
-
17M.1.SL.TZ1.T_9b:
Find the slant height, , of the cone.
-
17M.1.SL.TZ1.T_9c:
Find the curved surface area of the cone.
-
19M.2.SL.TZ2.T_3a:
Find the volume of one cone-shaped container.
-
19M.2.SL.TZ2.T_3b:
Find the slant height of the cone-shaped container.
-
19M.2.SL.TZ2.T_3c:
Show that the total surface area of the cone-shaped container is 314 cm2, correct to three significant figures.
-
19M.2.SL.TZ2.T_3d:
Find the height, , of this cylinder-shaped container.
-
19M.2.SL.TZ2.T_3e:
The factory director wants to increase the volume of coconut water sold per container.
State whether or not they should replace the cone-shaped containers with cylinder‑shaped containers. Justify your conclusion.
-
18N.1.SL.TZ0.T_9a.i:
Write down the value of x.
-
18N.1.SL.TZ0.T_9a.ii:
Calculate the volume of the paperweight.
-
18N.1.SL.TZ0.T_9b:
1 cm3 of glass has a mass of 2.56 grams.
Calculate the mass, in grams, of the paperweight.
-
19M.1.SL.TZ1.T_1c:
Find the volume, in cm3, of this calculator case.
-
18M.2.SL.TZ1.T_1a:
Calculate the area of triangle EAD.
-
18M.2.SL.TZ1.T_1b:
Calculate the total volume of the barn.
-
18M.2.SL.TZ1.T_1c:
Calculate the length of MN.
-
18M.2.SL.TZ1.T_1d:
Calculate the length of AE.
-
18M.2.SL.TZ1.T_1e:
Show that Farmer Brown is incorrect.
-
18M.2.SL.TZ1.T_1f:
Calculate the total length of metal required for one support.
-
17N.2.SL.TZ0.T_6a:
Show that the volume of a cone shaped glass is , correct to 3 significant figures.
-
17N.2.SL.TZ0.T_6b:
Calculate the radius, , of a hemisphere shaped glass.
-
17N.2.SL.TZ0.T_6c:
Find the cost of of chocolate mousse.
-
17N.2.SL.TZ0.T_6d:
Show that there is of orange paste in each special dessert.
-
17N.2.SL.TZ0.T_6e:
Find the total cost of the ingredients of one special dessert.
-
17N.2.SL.TZ0.T_6f:
Find the value of .
-
17M.1.SL.TZ2.T_12a:
Find the volume of water in the container.
-
17M.1.SL.TZ2.T_12b:
Find the value of .
-
19M.1.SL.TZ1.T_15a:
Write down an equation for the area, , of the curved surface in terms of .
-
19M.1.SL.TZ1.T_15b:
Find .
-
19M.1.SL.TZ1.T_15c:
Find the value of when the area of the curved surface is maximized.
-
16N.1.SL.TZ0.T_7a:
Calculate the volume of the balloon.
-
16N.1.SL.TZ0.T_7b:
Calculate the radius of the balloon following this increase.
-
20N.1.SL.TZ0.T_1a:
Write down the value of the iron in the form where .
-
20N.1.SL.TZ0.T_1b:
Calculate James’s estimate of its volume, in .
-
20N.1.SL.TZ0.T_1c:
The actual volume of the asteroid is found to be .
Find the percentage error in James’s estimate of the volume.
-
21M.1.SL.TZ1.2a:
Write down the radius of the planet.
-
21M.1.SL.TZ1.2b:
The volume of the planet can be expressed in the form where and .
Find the value of and the value of .
-
21M.1.SL.TZ2.8c:
Find the value of .
-
21M.1.SL.TZ2.8d:
Hence, find the volume of the cone.
-
22M.1.AHL.TZ1.11a:
Show that the three planes do not intersect.
-
22M.1.AHL.TZ1.11b.i:
Verify that the point lies on both and .
-
22M.1.AHL.TZ1.11b.ii:
Find a vector equation of , the line of intersection of and .
-
22M.1.AHL.TZ1.11c:
Find the distance between and .
-
22M.2.SL.TZ1.7a:
Find .
-
22M.2.SL.TZ1.7c:
Find the height of the pyramid, .
-
22M.2.SL.TZ1.7d:
A second ornament is in the shape of a cuboid with a rectangular base of length , width and height . The cuboid has the same volume as the pyramid.
The cuboid has a minimum surface area of . Find the value of .
SL 3.2—2d and 3d trig, sine rule, cosine rule, area
-
SPM.1.SL.TZ0.1a:
Given that find the value of .
-
SPM.1.SL.TZ0.1b:
Find the area of triangle ABC.
-
SPM.2.SL.TZ0.7a:
Find the distance from point A to point B.
-
SPM.2.SL.TZ0.7b.i:
Show that is 101°.
-
SPM.2.SL.TZ0.7b.ii:
Find the distance from the camp to point C.
-
SPM.2.SL.TZ0.7c:
Find .
-
SPM.2.SL.TZ0.7d:
Find the bearing that Jacob must take to point C.
-
SPM.2.SL.TZ0.7e:
Jacob hikes at an average speed of 3.9 km/h.
Find, to the nearest minute, the time it takes for Jacob to reach point C.
-
18N.2.AHL.TZ0.H_11a:
Find an expression for in terms of .
-
18N.2.AHL.TZ0.H_11b:
Show that .
-
18N.2.AHL.TZ0.H_11c:
By sketching the graph of as a function of , determine the range of values of for which there are possible values of .
-
18M.2.SL.TZ2.T_5a.i:
Use Giovanni’s diagram to show that angle ABC, the angle at which the Tower is leaning relative to the
horizontal, is 85° to the nearest degree. -
18M.2.SL.TZ2.T_5a.ii:
Use Giovanni's diagram to calculate the length of AX.
-
18M.2.SL.TZ2.T_5a.iii:
Use Giovanni's diagram to find the length of BX, the horizontal displacement of the Tower.
-
18M.2.SL.TZ2.T_5b:
Find the percentage error on Giovanni’s diagram.
-
18M.2.SL.TZ2.T_5c:
Giovanni adds a point D to his diagram, such that BD = 45 m, and another triangle is formed.
Find the angle of elevation of A from D.
-
17N.2.SL.TZ0.T_3a:
Show that correct to the nearest metre.
-
17N.2.SL.TZ0.T_3b:
Calculate angle .
-
17N.2.SL.TZ0.T_3c:
Find the area of ABCD.
-
17N.2.SL.TZ0.T_3d.i:
Calculate Abdallah’s estimate for the area.
-
17N.2.SL.TZ0.T_3d.ii:
Find the percentage error in Abdallah’s estimate.
-
19M.2.SL.TZ1.T_2a:
Find the length , giving your answer to four significant figures.
-
19M.2.SL.TZ1.T_2b:
Find the total area of the two rectangles that make up the roof.
-
19M.2.SL.TZ1.T_2c:
Find the maximum number of complete panels that can be fitted to the whole roof.
-
19M.2.SL.TZ1.T_2d:
Find the percentage error in her estimate.
-
19M.2.SL.TZ1.T_2e:
Olivia investigates arranging the panels, such that the longer edge of each panel is parallel to or .
State whether this new arrangement will allow Olivia to fit more solar panels to the roof. Justify your answer. -
18M.1.SL.TZ2.T_8a:
Calculate the length of side AC in km.
-
18M.1.SL.TZ2.T_8b:
Calculate the area of the park.
-
19M.2.SL.TZ2.T_2a:
Find the distance from A to C.
-
19M.2.SL.TZ2.T_2b.i:
Find the size of angle .
-
19M.2.SL.TZ2.T_2b.ii:
Find the size of angle .
-
19M.2.SL.TZ2.T_2c:
Find the size of angle .
-
19M.2.SL.TZ2.T_2d:
The length of path AD is 287 m.
Find the area of the region ABCD.
-
17M.2.AHL.TZ2.H_4a:
Find the set of values of that satisfy the inequality .
-
17M.2.AHL.TZ2.H_4b:
The triangle ABC is shown in the following diagram. Given that , find the range of possible values for AB.

-
19M.2.AHL.TZ2.H_1:
In triangle ABC, AB = 5, BC = 14 and AC = 11.
Find all the interior angles of the triangle. Give your answers in degrees to one decimal place.
-
19M.1.AHL.TZ1.H_4a:
Show that .
-
19M.1.AHL.TZ1.H_4b:
Find the two possible values for the length of the third side.
-
17N.1.SL.TZ0.S_4a:
Show that .
-
17N.1.SL.TZ0.S_4b:
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

Find the exact perimeter of this shape.
-
17M.1.SL.TZ1.S_3:
The following diagram shows triangle PQR.

Find PR.
-
19M.1.SL.TZ1.S_3c:
Hence or otherwise, find .
-
18M.2.SL.TZ2.S_2a:
Find DB.
-
18M.2.SL.TZ2.S_2b:
Find DC.
-
18N.2.SL.TZ0.S_7a:
Let SR = . Use the cosine rule to show that .
-
18N.2.SL.TZ0.S_7b:
Hence or otherwise, find the total distance along the road where the signal from the tower can reach cellular phones.
-
19M.2.SL.TZ2.S_3a:
Find BD.
-
19M.2.SL.TZ2.S_3b:
The area of triangle ABD is 18.5 cm2. Find the possible values of θ.
-
17N.2.SL.TZ0.S_1a:
Find BC.
-
17N.2.SL.TZ0.S_1b:
Find the area of triangle ABC.
-
18M.2.SL.TZ1.T_1a:
Calculate the area of triangle EAD.
-
18M.2.SL.TZ1.T_1b:
Calculate the total volume of the barn.
-
18M.2.SL.TZ1.T_1c:
Calculate the length of MN.
-
18M.2.SL.TZ1.T_1d:
Calculate the length of AE.
-
18M.2.SL.TZ1.T_1e:
Show that Farmer Brown is incorrect.
-
18M.2.SL.TZ1.T_1f:
Calculate the total length of metal required for one support.
-
17N.1.SL.TZ0.T_10a:
Find the length of EB.
-
17N.1.SL.TZ0.T_10b:
Write down the angle of elevation of B from E.
-
17N.1.SL.TZ0.T_10c:
Find the vertical height of B above the ground.
-
17M.2.SL.TZ1.T_2a.i:
Write down an equation for the area of ABCDE using the above information.
-
17M.2.SL.TZ1.T_2a.ii:
Show that the equation in part (a)(i) simplifies to .
-
17M.2.SL.TZ1.T_2b:
Find the length of CD.
-
17M.2.SL.TZ1.T_2c:
Show that angle , correct to one decimal place.
-
17M.2.SL.TZ1.T_2d:
Find the length of the perimeter of ABCDE.
-
17M.2.SL.TZ1.T_2e:
Calculate the length of CF.
-
19M.1.SL.TZ2.T_9a:
Find the angle of elevation from B to C.
-
19M.1.SL.TZ2.T_9b:
A second truck arrives whose ladder, when fully extended, is 30 metres long. The base of this ladder is also 4 metres above the ground. For safety reasons, the maximum angle of elevation that the ladder can make is 70º.
Find the maximum height on the wall that can be reached by the ladder on the second truck.
-
17M.1.SL.TZ2.T_3a:
Find the length of one of the straight pieces in the wireframe.
-
17M.1.SL.TZ2.T_3b:
Find the total length of wire needed to construct this wireframe. Give your answer in centimetres correct to the nearest millimetre.
-
18N.2.SL.TZ0.T_5a:
Show that the size of angle BÂC is 20.2°, correct to 3 significant figures.
-
18N.2.SL.TZ0.T_5b:
Calculate the area of triangle ABC.
-
18N.2.SL.TZ0.T_5c:
Find the length of AC.
-
18N.2.SL.TZ0.T_5d:
A vertical pole, TB, is constructed at point B and has height 25 m.
Calculate the angle of elevation of T from, M, the midpoint of the side AC.
-
19M.1.SL.TZ1.T_8a:
Draw and label the angle of depression on the diagram.
-
16N.1.SL.TZ0.T_11a:
Calculate CD, the height of the observation deck above the ground.
-
16N.1.SL.TZ0.T_11b:
Calculate the angle of depression from A to B.
-
18M.1.SL.TZ1.T_8a:
On the diagram, draw and label with an x the angle of depression of B from P.
-
18M.1.SL.TZ1.T_8b:
Find the size of angle APB.
-
18M.1.SL.TZ1.T_8c:
Find the size of the angle of depression of B from P.
-
17M.2.SL.TZ2.T_4a:
Find the length of the path BD.
-
17M.2.SL.TZ2.T_4b:
Show that angle DBC is 48.7°, correct to three significant figures.
-
17M.2.SL.TZ2.T_4c:
Find the area of the park.
-
17M.2.SL.TZ2.T_4d:
Find the length of the path CE.
-
17M.2.SL.TZ2.T_4e:
Calculate the total length of the track.
-
19M.1.SL.TZ1.T_10a:
Find the size, in degrees, of angle BÂC.
-
19M.1.SL.TZ1.T_10b:
Find the area, in km2, of triangle ABC.
-
16N.2.SL.TZ0.T_5a:
the length of BD;
-
16N.2.SL.TZ0.T_5b:
the size of angle DAB;
-
16N.2.SL.TZ0.T_5c:
the area of triangle ABD;
-
16N.2.SL.TZ0.T_5d:
the area of quadrilateral ABCD;
-
16N.2.SL.TZ0.T_5e:
the length of AP;
-
16N.2.SL.TZ0.T_5f:
the length of the fence, BP.
-
17M.1.SL.TZ1.T_13a:
Find the length of BC.
-
17M.1.SL.TZ1.T_13b:
Find the area of the postage stamp.
-
19N.1.AHL.TZ0.H_9a:
Given that , show that .
-
19N.1.AHL.TZ0.H_9b:
Show that .
-
19N.1.AHL.TZ0.H_9c.i:
By considering triangle , show that .
-
19N.1.AHL.TZ0.H_9c.ii:
By considering triangle , find another expression for in terms of and .
-
19N.1.AHL.TZ0.H_9d:
Use your answers to part (c) to show that .
-
19N.1.SL.TZ0.S_9a.i:
.
-
19N.1.SL.TZ0.S_9a.ii:
.
-
19N.1.SL.TZ0.S_9b:
Given that , show that .
-
19N.1.SL.TZ0.S_9c:
Calculate the area of triangle .
-
19N.2.SL.TZ0.S_6:
The diagram below shows a triangular-based pyramid with base .
Edge is perpendicular to the edges and ., , , ,
Calculate
-
20N.1.SL.TZ0.S_2a:
Given that is acute, find .
-
20N.1.SL.TZ0.S_2b:
Find .
-
20N.2.SL.TZ0.T_3a:
Calculate the length of .
-
20N.2.SL.TZ0.T_3b:
Show that angle , correct to three significant figures.
-
20N.2.SL.TZ0.T_3c:
Calculate the area of triangle .
-
20N.2.SL.TZ0.T_3d:
Pedro draws a circle, with centre at point , passing through point . Part of the circle is shown in the diagram.
Show that point lies outside this circle. Justify your reasoning.
-
EXN.1.AHL.TZ0.7:
Consider quadrilateral where is parallel to .
In , , , and .
Find an expression for in terms of and .
-
EXN.2.SL.TZ0.2a:
Show that arc has length .
-
EXN.2.SL.TZ0.2b:
Show that .
-
21M.2.SL.TZ1.8a:
Write down an expression for in terms of .
-
21M.2.SL.TZ1.8b:
Show that the area of the field that the horse can reach is .
-
21M.2.SL.TZ1.8c:
The area of field that the horse can reach is . Find the value of .
-
21M.2.SL.TZ1.8d:
Hence, find the size of .
-
21M.2.SL.TZ1.8e.i:
Find the size of .
-
21M.2.SL.TZ1.8e.ii:
Find the length of new fence required.
-
21M.3.AHL.TZ1.2c:
Show that .
-
21M.3.AHL.TZ1.2d:
Use the results from parts (b) and (c) to show that .
-
21M.1.SL.TZ2.6:
The following diagram shows triangle , with , and .
Given that , find the area of the triangle.
Give your answer in the form where .
-
19M.1.SL.TZ1.S_3a:
Given that , find the value of .
-
19M.1.SL.TZ1.S_3b:
Find the value of .
-
21N.2.SL.TZ0.3:
Consider a triangle , where and .
Find the smallest possible perimeter of triangle .
-
21N.2.SL.TZ0.5a:
Given that the areas of the two shaded regions are equal, show that .
-
21N.2.SL.TZ0.5b:
Hence determine the value of .
-
22M.2.SL.TZ1.7b:
Given that , find .
-
22M.2.SL.TZ2.1a:
Find the length of the chord .
-
22M.2.SL.TZ2.1b:
Find the area of the shaded sector.
-
22M.2.SL.TZ2.7a:
Find the distance from point to point .
-
22M.2.SL.TZ2.7b:
Find the area of this piece of land.
-
22M.2.SL.TZ2.7c:
Find .
-
22M.2.SL.TZ2.7d:
Find the distance from point to point .
SL 3.3—Applications: angles of elevation and depression, bearings
-
SPM.2.SL.TZ0.7a:
Find the distance from point A to point B.
-
SPM.2.SL.TZ0.7b.i:
Show that is 101°.
-
SPM.2.SL.TZ0.7b.ii:
Find the distance from the camp to point C.
-
SPM.2.SL.TZ0.7c:
Find .
-
SPM.2.SL.TZ0.7d:
Find the bearing that Jacob must take to point C.
-
SPM.2.SL.TZ0.7e:
Jacob hikes at an average speed of 3.9 km/h.
Find, to the nearest minute, the time it takes for Jacob to reach point C.
-
17N.2.AHL.TZ0.H_5:
Barry is at the top of a cliff, standing 80 m above sea level, and observes two yachts in the sea.
“Seaview” is at an angle of depression of 25°.
“Nauti Buoy” is at an angle of depression of 35°.
The following three dimensional diagram shows Barry and the two yachts at S and N.
X lies at the foot of the cliff and angle 70°.
Find, to 3 significant figures, the distance between the two yachts.
-
17N.1.SL.TZ0.S_4a:
Show that .
-
17N.1.SL.TZ0.S_4b:
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

Find the exact perimeter of this shape.
-
17M.1.SL.TZ1.S_3:
The following diagram shows triangle PQR.

Find PR.
-
18N.2.SL.TZ0.S_7a:
Let SR = . Use the cosine rule to show that .
-
18N.2.SL.TZ0.S_7b:
Hence or otherwise, find the total distance along the road where the signal from the tower can reach cellular phones.
-
19M.2.SL.TZ2.S_3a:
Find BD.
-
19M.2.SL.TZ2.S_3b:
The area of triangle ABD is 18.5 cm2. Find the possible values of θ.
-
17N.1.SL.TZ0.T_10b:
Write down the angle of elevation of B from E.
-
19M.1.SL.TZ2.T_9a:
Find the angle of elevation from B to C.
-
18N.2.SL.TZ0.T_5d:
A vertical pole, TB, is constructed at point B and has height 25 m.
Calculate the angle of elevation of T from, M, the midpoint of the side AC.
-
19M.1.SL.TZ1.T_8a:
Draw and label the angle of depression on the diagram.
-
16N.1.SL.TZ0.T_11a:
Calculate CD, the height of the observation deck above the ground.
-
16N.1.SL.TZ0.T_11b:
Calculate the angle of depression from A to B.
-
18M.1.SL.TZ1.T_8a:
On the diagram, draw and label with an x the angle of depression of B from P.
-
21M.2.SL.TZ1.8e.i:
Find the size of .
-
21M.2.SL.TZ1.8e.ii:
Find the length of new fence required.
-
21M.2.SL.TZ2.7a:
Given that point is metres from the base of the windmill, find the height of point above the ground.
-
21M.2.SL.TZ2.7b:
Find the angle of elevation of point from point .
-
21M.2.SL.TZ2.7c:
Find the length of each blade of the windmill.
-
22M.2.AHL.TZ2.11a:
Find the three-figure bearing on which airplane is travelling.
SL 3.4—Circle: radians, arcs, sectors
-
SPM.2.SL.TZ0.2a:
Find the value of θ, giving your answer in radians.
-
SPM.2.SL.TZ0.2b:
Find the area of the shaded region.
-
18M.2.AHL.TZ2.H_4a.i:
Find AM.
-
18M.2.AHL.TZ2.H_4a.ii:
Find in radians.
-
18M.2.AHL.TZ2.H_4b:
Find the area of the shaded region.
-
17N.2.AHL.TZ0.H_3:
This diagram shows a metallic pendant made out of four equal sectors of a larger circle of radius and four equal sectors of a smaller circle of radius .
The angle 20°.
Find the area of the pendant.
-
16N.2.AHL.TZ0.H_9a:
Find an expression for the shaded area in terms of , and .
-
16N.2.AHL.TZ0.H_9b:
Show that .
-
16N.2.AHL.TZ0.H_9c:
Hence find the value of given that the shaded area is equal to 4.
-
19M.1.AHL.TZ1.H_3:
A sector of a circle with radius cm , where > 0, is shown on the following diagram.
The sector has an angle of 1 radian at the centre.Let the area of the sector be cm2 and the perimeter be cm. Given that , find the value of .
-
17M.2.AHL.TZ1.H_8a:
Find an expression for the volume of water in the trough in terms of .
-
17M.2.AHL.TZ1.H_8b:
Calculate when .
-
18N.2.AHL.TZ0.H_7:
Boat A is situated 10km away from boat B, and each boat has a marine radio transmitter on board. The range of the transmitter on boat A is 7km, and the range of the transmitter on boat B is 5km. The region in which both transmitters can be detected is represented by the shaded region in the following diagram. Find the area of this region.
-
19M.2.SL.TZ2.S_4a:
Show that .
-
19M.2.SL.TZ2.S_4b:
Find the area of triangle OBC in terms of and θ.
-
19M.2.SL.TZ2.S_4c:
Given that the area of triangle OBC is of the area of sector OAB, find θ.
-
17N.1.SL.TZ0.S_4a:
Show that .
-
17N.1.SL.TZ0.S_4b:
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

Find the exact perimeter of this shape.
-
17M.2.SL.TZ1.S_5:
The following diagram shows the chord [AB] in a circle of radius 8 cm, where .

Find the area of the shaded segment.
-
17M.2.SL.TZ2.S_1a:
Find the length of arc ABC.
-
17M.2.SL.TZ2.S_1b:
Find the perimeter of sector OABC.
-
17M.2.SL.TZ2.S_1c:
Find the area of sector OABC.
-
16N.2.SL.TZ0.S_3a:
Write down the exact value of in radians.
-
16N.2.SL.TZ0.S_3b:
Find the value of .
-
16N.2.SL.TZ0.S_3c:
Find AB.
-
18M.2.SL.TZ1.S_3a:
Find the area of the shaded region, in terms of θ.
-
18M.2.SL.TZ1.S_3b:
The area of the shaded region is 12 cm2. Find the value of θ.
-
18M.1.SL.TZ2.S_4:
The following diagram shows a circle with centre O and radius r cm.
The points A and B lie on the circumference of the circle, and = θ. The area of the shaded sector AOB is 12 cm2 and the length of arc AB is 6 cm.
Find the value of r.
-
19N.2.AHL.TZ0.H_4a:
the perimeter.
-
19N.2.AHL.TZ0.H_4b:
the area.
-
19N.2.SL.TZ0.S_4a:
Find .
-
19N.2.SL.TZ0.S_4b:
Find the area of .
-
20N.2.AHL.TZ0.H_11a:
Find the times when comes to instantaneous rest.
-
20N.2.AHL.TZ0.H_11b:
Find an expression for in terms of .
-
20N.2.AHL.TZ0.H_11c:
Find the maximum displacement of , in metres, from its initial position.
-
20N.2.AHL.TZ0.H_11d:
Find the total distance travelled by in the first seconds of its motion.
-
20N.2.AHL.TZ0.H_11e.i:
Show that, at these times, .
-
20N.2.AHL.TZ0.H_11e.ii:
Hence show that .
-
20N.2.SL.TZ0.S_7a:
Show that .
-
20N.2.SL.TZ0.S_7b:
Find the value of when the area of the shaded region is equal to the area of sector .
-
EXN.2.SL.TZ0.2a:
Show that arc has length .
-
EXN.2.SL.TZ0.2b:
Show that .
-
21M.2.SL.TZ1.8a:
Write down an expression for in terms of .
-
21M.2.SL.TZ1.8b:
Show that the area of the field that the horse can reach is .
-
21M.2.SL.TZ1.8c:
The area of field that the horse can reach is . Find the value of .
-
21M.2.SL.TZ1.8d:
Hence, find the size of .
-
21M.2.SL.TZ1.8e.i:
Find the size of .
-
21M.2.SL.TZ1.8e.ii:
Find the length of new fence required.
-
21M.3.AHL.TZ1.2c:
Show that .
-
21M.3.AHL.TZ1.2d:
Use the results from parts (b) and (c) to show that .
-
21M.1.SL.TZ2.1a:
Find the value of .
-
21M.1.SL.TZ2.1b:
Hence, find the exact area of the non-shaded region.
-
21N.2.SL.TZ0.5a:
Given that the areas of the two shaded regions are equal, show that .
-
21N.2.SL.TZ0.5b:
Hence determine the value of .
-
22M.2.SL.TZ1.3a:
Find the area of one of the shaded segments in terms of .
-
22M.2.SL.TZ1.3b:
Given that the area of the logo is , find the value of .
-
22M.2.SL.TZ2.1a:
Find the length of the chord .
-
22M.2.SL.TZ2.1b:
Find the area of the shaded sector.
SL 3.5—Unit circle definitions of sin, cos, tan. Exact trig ratios, ambiguous case of sine rule
-
16N.1.AHL.TZ0.H_13a:
Find the value of .
-
16N.1.AHL.TZ0.H_13d:
Hence or otherwise solve the equation in the interval .
-
16N.2.AHL.TZ0.H_7a:
Use the cosine rule to find the two possible values for AC.
-
16N.2.AHL.TZ0.H_7b:
Find the difference between the areas of the two possible triangles ABC.
-
19M.1.AHL.TZ1.H_4a:
Show that .
-
19M.1.AHL.TZ1.H_4b:
Find the two possible values for the length of the third side.
-
17N.1.SL.TZ0.S_4a:
Show that .
-
17N.1.SL.TZ0.S_4b:
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

Find the exact perimeter of this shape.
-
17M.1.SL.TZ1.S_3:
The following diagram shows triangle PQR.

Find PR.
-
19M.1.SL.TZ2.S_9a:
Find the value of .
-
18M.2.SL.TZ1.S_6:
Triangle ABC has a = 8.1 cm, b = 12.3 cm and area 15 cm2. Find the largest possible perimeter of triangle ABC.
-
18N.2.SL.TZ0.S_7a:
Let SR = . Use the cosine rule to show that .
-
18N.2.SL.TZ0.S_7b:
Hence or otherwise, find the total distance along the road where the signal from the tower can reach cellular phones.
-
19M.2.SL.TZ2.S_3a:
Find BD.
-
19M.2.SL.TZ2.S_3b:
The area of triangle ABD is 18.5 cm2. Find the possible values of θ.
-
19N.1.AHL.TZ0.H_9a:
Given that , show that .
-
19N.1.AHL.TZ0.H_9b:
Show that .
-
19N.1.AHL.TZ0.H_9c.i:
By considering triangle , show that .
-
19N.1.AHL.TZ0.H_9c.ii:
By considering triangle , find another expression for in terms of and .
-
19N.1.AHL.TZ0.H_9d:
Use your answers to part (c) to show that .
-
21N.2.SL.TZ0.3:
Consider a triangle , where and .
Find the smallest possible perimeter of triangle .
-
22M.1.SL.TZ1.4b:
Solve the equation where .
-
22M.1.SL.TZ1.9b.i:
Show that , where is a positive real constant.
-
22M.1.SL.TZ1.9b.ii:
It is given that , where . Find the value of .
-
22M.1.AHL.TZ1.9b:
Hence, given that , find the value of .
-
22M.1.SL.TZ2.5:
Find the least positive value of for which .
-
22M.1.AHL.TZ2.7:
By using the substitution or otherwise, find an expression for in terms of , where is a non-zero real number.
-
22M.2.AHL.TZ2.7a:
Show that a finite limit only exists for .
-
22M.2.AHL.TZ2.7b:
Using l’Hôpital’s rule, show algebraically that the value of the limit is .
SL 3.6—Pythagorean identity, double angles
-
SPM.1.SL.TZ0.1a:
Given that find the value of .
-
SPM.1.SL.TZ0.1b:
Find the area of triangle ABC.
-
SPM.1.SL.TZ0.6a:
Show that .
-
SPM.1.SL.TZ0.6b:
Hence or otherwise solve for .
-
16N.1.AHL.TZ0.H_13b:
Show that where .
-
16N.1.AHL.TZ0.H_13c:
Use the principle of mathematical induction to prove that
where .
-
16N.1.AHL.TZ0.H_13d:
Hence or otherwise solve the equation in the interval .
-
17M.1.SL.TZ1.S_10a:
Show that .
-
17M.1.SL.TZ1.S_10b:
Given that , find .
-
17M.1.SL.TZ1.S_10c:
Let , for . The graph of between and is rotated 360° about the -axis. Find the volume of the solid formed.
-
17M.1.SL.TZ2.S_7:
Solve , for .
-
19M.1.SL.TZ2.S_9a:
Find the value of .
-
16N.1.SL.TZ0.S_2a:
Find .
-
16N.1.SL.TZ0.S_2b:
Find .
-
18N.1.SL.TZ0.S_7:
Given that , where , find the value of .
-
20N.1.SL.TZ0.S_2a:
Given that is acute, find .
-
20N.1.SL.TZ0.S_2b:
Find .
-
21M.1.SL.TZ1.6a:
Show that .
-
21M.1.SL.TZ1.6b:
Hence or otherwise, solve for .
-
21M.1.AHL.TZ1.12a:
Show that .
-
21M.1.SL.TZ2.3a:
Show that the equation may be written in the form .
-
21M.1.SL.TZ2.3b:
Hence, solve the equation .
-
22M.1.SL.TZ1.4b:
Solve the equation where .
-
22M.1.SL.TZ1.9a.ii:
By using a suitable substitution for , show that .
SL 3.7—Circular functions: graphs, composites, transformations
-
SPM.2.SL.TZ0.9a:
Find the period of .
-
SPM.2.SL.TZ0.9b.i:
Find the value of .
-
SPM.2.SL.TZ0.9b.ii:
Hence, find the value of (6).
-
SPM.2.SL.TZ0.9c:
Find the value of and the value of .
-
SPM.2.SL.TZ0.9d:
Find the value of for which the functions have the greatest difference.
-
EXM.3.AHL.TZ0.5a.i:
Sketch the graph , for
-
EXM.3.AHL.TZ0.5a.ii:
Write down the amplitude of this graph
-
EXM.3.AHL.TZ0.5a.iii:
Write down the period of this graph
-
EXM.3.AHL.TZ0.5b.i:
Use your answers from part (a) to write down the value of , and .
-
EXM.3.AHL.TZ0.5b.ii:
Find the value of .
-
EXM.3.AHL.TZ0.5c.i:
Find , giving the answer to 3 significant figures.
-
EXM.3.AHL.TZ0.5c.ii:
Comment on your answer to part (c)(i).
-
EXM.3.AHL.TZ0.5d:
By considering the graph of , find the value of , , and .
-
EXM.3.AHL.TZ0.5e.i:
.
-
EXM.3.AHL.TZ0.5e.ii:
.
-
EXM.3.AHL.TZ0.5e.iii:
.
-
EXM.3.AHL.TZ0.5e.iv:
.
-
EXM.3.AHL.TZ0.5f.i:
Show that .
-
EXM.3.AHL.TZ0.5f.ii:
Show that .
-
EXM.3.AHL.TZ0.5g:
Hence prove your conjectures in part (e).
-
19M.2.AHL.TZ1.H_10a:
Write down the maximum and minimum value of .
-
19M.2.AHL.TZ1.H_10b:
Write down two transformations that will transform the graph of onto the graph of .
-
19M.2.AHL.TZ1.H_10c:
Sketch the graph of for 0 ≤ ≤ 0.02 , showing clearly the coordinates of the first maximum and the first minimum.
-
19M.2.AHL.TZ1.H_10d:
Find the total time in the interval 0 ≤ ≤ 0.02 for which ≥ 3.
-
19M.2.AHL.TZ1.H_10e:
Find (0.007).
-
19M.2.AHL.TZ1.H_10f:
With reference to your graph of explain why > 0 for all > 0.
-
19M.2.AHL.TZ1.H_10g:
Given that can be written as where , , , > 0, use your graph to find the values of , , and .
-
19M.1.AHL.TZ2.H_9a:
Find the -coordinates of the points of intersection of the two graphs.
-
19M.1.AHL.TZ2.H_9b:
Find the exact area of the shaded region, giving your answer in the form , where , .
-
19M.1.AHL.TZ2.H_9c:
At the points A and B on the diagram, the gradients of the two graphs are equal.
Determine the -coordinate of A on the graph of .
-
19M.1.SL.TZ2.S_7b:
Consider the graph of , 0 ≤ < , where > 0.
Find the greatest value of such that the graph of does not intersect the line .
-
17N.2.SL.TZ0.S_10a:
Show that .
-
17N.2.SL.TZ0.S_10b.i:
Find the coordinates of and of .
-
17N.2.SL.TZ0.S_10b.ii:
Find the equation of .
-
17N.2.SL.TZ0.S_10c:
Show that the distance between the -coordinates of and is .
-
17N.2.SL.TZ0.S_10d:
A saw has a toothed edge which is 300 mm long. Find the number of complete teeth on this saw.
-
17M.2.SL.TZ1.S_8a.i:
How much time is there between the first low tide and the next high tide?
-
17M.2.SL.TZ1.S_8a.ii:
Find the difference in height between low tide and high tide.
-
17M.2.SL.TZ1.S_8b.i:
Find the value of ;
-
17M.2.SL.TZ1.S_8b.ii:
Find the value of ;
-
17M.2.SL.TZ1.S_8b.iii:
Find the value of .
-
17M.2.SL.TZ1.S_8c:
There are two high tides on 12 December 2017. At what time does the second high tide occur?
-
18M.2.SL.TZ1.S_10a:
Find the coordinates of A.
-
18M.2.SL.TZ1.S_10b.i:
For the graph of , write down the amplitude.
-
18M.2.SL.TZ1.S_10b.ii:
For the graph of , write down the period.
-
18M.2.SL.TZ1.S_10c:
Hence, write in the form .
-
18M.2.SL.TZ1.S_10d:
Find the maximum speed of the ball.
-
18M.2.SL.TZ1.S_10e:
Find the first time when the ball’s speed is changing at a rate of 2 cm s−2.
-
17M.2.SL.TZ2.S_4a:
Find the value of .
-
17M.2.SL.TZ2.S_4b:
Find the value of .
-
17M.2.SL.TZ2.S_4c:
Use the model to find the depth of the water 10 hours after high tide.
-
19M.2.SL.TZ1.S_8a:
The range of is ≤ ≤ . Find and .
-
19M.2.SL.TZ1.S_8b:
Find the range of .
-
19M.2.SL.TZ1.S_8c.i:
Find the value of and of .
-
19M.2.SL.TZ1.S_8c.ii:
Find the period of .
-
19M.2.SL.TZ1.S_8d:
The equation has two solutions where ≤ ≤ . Find both solutions.
-
16N.2.SL.TZ0.S_10a:
(i) Find the value of .
(ii) Show that .
(iii) Find the value of .
-
16N.2.SL.TZ0.S_10b:
(i) Write down the value of .
(ii) Find .
-
16N.2.SL.TZ0.S_10c:
(i) Find .
(ii) Hence or otherwise, find the maximum positive rate of change of .
-
20N.2.SL.TZ0.S_8a.i:
Find the height of point above the ground.
-
20N.2.SL.TZ0.S_8a.ii:
Calculate the number of seconds it takes for the water wheel to complete one rotation.
-
20N.2.SL.TZ0.S_8a.iii:
Hence find the number of rotations the water wheel makes in one hour.
-
20N.2.SL.TZ0.S_8b:
Find .
-
20N.2.SL.TZ0.S_8c:
Find .
-
20N.2.SL.TZ0.S_8d:
Determine the rate of change of when the top of the bucket is at .
-
EXN.1.SL.TZ0.9a:
Find the height of the ball above the ground when it is released.
-
EXN.1.SL.TZ0.9b:
Find the minimum height of the ball above the ground.
-
EXN.1.SL.TZ0.9c:
Show that the ball takes seconds to return to its initial height above the ground for the first time.
-
EXN.1.SL.TZ0.9d:
For the first 2 seconds of its motion, determine the amount of time that the ball is less than metres above the ground.
-
21M.2.SL.TZ1.4:
A Ferris wheel with diameter metres rotates at a constant speed. The lowest point on the wheel is metres above the ground, as shown on the following diagram. is a point on the wheel. The wheel starts moving with at the lowest point and completes one revolution in minutes.
The height, metres, of above the ground after minutes is given by , where .
Find the values of , and .
-
21M.1.SL.TZ2.8a:
Find the -coordinates of and .
-
21M.2.SL.TZ2.7d:
Find the value of and the value of .
-
21M.2.SL.TZ2.7e:
If the observer stands directly under point for one minute, point will pass over his head times.
Find the value of .
-
21N.2.SL.TZ0.8a:
Show that .
-
21N.2.SL.TZ0.8b:
Find the value of .
-
21N.2.SL.TZ0.8c:
Find the value of .
-
21N.2.SL.TZ0.8d:
Find the smallest possible value of .
-
21N.2.SL.TZ0.8e:
Find the height of the water at .
-
21N.2.SL.TZ0.8f:
Determine the number of hours, over a 24-hour period, for which the tide is higher than metres.
-
21N.2.AHL.TZ0.9a:
Show that .
-
21N.2.AHL.TZ0.9b:
Find the value of .
-
21N.2.AHL.TZ0.9c:
Find the value of .
-
21N.2.AHL.TZ0.9d:
Find the smallest possible value of .
-
21N.2.AHL.TZ0.9e:
Find the height of the water at .
-
21N.2.AHL.TZ0.9f:
Determine the number of hours, over a 24-hour period, for which the tide is higher than metres.
-
21N.2.AHL.TZ0.9g:
A fisherman notes that the water height at nearby Folkestone harbour follows the same sinusoidal pattern as that of Dungeness harbour, with the exception that high tides (and low tides) occur minutes earlier than at Dungeness.
Find a suitable equation that may be used to model the tidal height of water at Folkestone harbour.
-
22M.1.SL.TZ1.6a:
Describe these two transformations.
-
22M.1.SL.TZ1.6b:
The -intercept of the graph of is at .
Given that , find the smallest value of .
-
22M.2.SL.TZ2.8b:
Find the values of when .
-
22M.2.AHL.TZ2.10b:
Find the values of when .
SL 3.8—Solving trig equations
-
16N.1.AHL.TZ0.H_13a:
Find the value of .
-
16N.1.AHL.TZ0.H_13d:
Hence or otherwise solve the equation in the interval .
-
17N.2.AHL.TZ0.H_11a.i:
Determine an expression for in terms of .
-
17N.2.AHL.TZ0.H_11a.ii:
Sketch a graph of for .
-
17N.2.AHL.TZ0.H_11a.iii:
Find the -coordinate(s) of the point(s) of inflexion of the graph of , labelling these clearly on the graph of .
-
17N.2.AHL.TZ0.H_11b.i:
Express in terms of .
-
17N.2.AHL.TZ0.H_11b.ii:
Express in terms of .
-
17N.2.AHL.TZ0.H_11b.iii:
Hence show that can be expressed as .
-
17N.2.AHL.TZ0.H_11c:
Solve the equation , giving your answers in the form where .
-
18M.1.AHL.TZ1.H_8:
Let .
Find, in terms of b, the solutions of .
-
18M.2.SL.TZ1.S_3a:
Find the area of the shaded region, in terms of θ.
-
18M.2.SL.TZ1.S_3b:
The area of the shaded region is 12 cm2. Find the value of θ.
-
19M.1.SL.TZ2.S_9a:
Find the value of .
-
19M.1.SL.TZ2.S_9d:
The following diagram shows the graph of for 0 ≤ ≤ 3. Line is a tangent to the graph of at point P.
Given that is parallel to , find the -coordinate of P.
-
19M.2.SL.TZ1.S_8a:
The range of is ≤ ≤ . Find and .
-
19M.2.SL.TZ1.S_8b:
Find the range of .
-
19M.2.SL.TZ1.S_8c.i:
Find the value of and of .
-
19M.2.SL.TZ1.S_8c.ii:
Find the period of .
-
19M.2.SL.TZ1.S_8d:
The equation has two solutions where ≤ ≤ . Find both solutions.
-
19N.1.SL.TZ0.S_6:
Let , for . Find the values of for which .
-
19N.2.SL.TZ0.S_10a:
Find an expression for the velocity, m s−1, of the rocket during the first stage.
-
19N.2.SL.TZ0.S_10b:
Find the distance that the rocket travels during the first stage.
-
19N.2.SL.TZ0.S_10c:
During the second stage, the rocket accelerates at a constant rate. The distance which the rocket travels during the second stage is the same as the distance it travels during the first stage.
Find the total time taken for the two stages.
-
21M.1.SL.TZ1.6a:
Show that .
-
21M.1.SL.TZ1.6b:
Hence or otherwise, solve for .
-
21M.1.SL.TZ2.3a:
Show that the equation may be written in the form .
-
21M.1.SL.TZ2.3b:
Hence, solve the equation .
-
21M.1.AHL.TZ2.2:
Solve the equation .
-
21N.1.SL.TZ0.6a:
Show that .
-
21N.1.SL.TZ0.6b:
Hence or otherwise, solve the equation for .
-
22M.1.SL.TZ1.4b:
Solve the equation where .
-
22M.1.SL.TZ2.5:
Find the least positive value of for which .
-
22M.2.SL.TZ1.3b:
Given that the area of the logo is , find the value of .
-
22M.2.SL.TZ2.8b:
Find the values of when .
-
22M.2.AHL.TZ2.10b:
Find the values of when .
AHL 3.9—Reciprocal trig ratios and their pythagorean identities. Inverse circular functions
-
SPM.2.AHL.TZ0.12a:
Show that .
-
SPM.2.AHL.TZ0.12b:
Verify that and satisfy the equation .
-
SPM.2.AHL.TZ0.12c:
Hence, or otherwise, show that the exact value of .
-
SPM.2.AHL.TZ0.12d:
Using the results from parts (b) and (c) find the exact value of .
Give your answer in the form where , .
-
SPM.3.AHL.TZ0.2a:
On the same set of axes, sketch the graphs of and for −1 ≤ ≤ 1.
-
SPM.3.AHL.TZ0.2b.i:
local maximum points;
-
SPM.3.AHL.TZ0.2b.ii:
local minimum points;
-
SPM.3.AHL.TZ0.2c:
On a new set of axes, sketch the graphs of and for −1 ≤ ≤ 1.
-
SPM.3.AHL.TZ0.2d.i:
local maximum points;
-
SPM.3.AHL.TZ0.2d.ii:
local minimum points.
-
SPM.3.AHL.TZ0.2e:
Solve the equation and hence show that the stationary points on the graph of occur at where and 0 < < .
-
SPM.3.AHL.TZ0.2f:
Use an appropriate trigonometric identity to show that .
-
SPM.3.AHL.TZ0.2g:
Use an appropriate trigonometric identity to show that .
-
SPM.3.AHL.TZ0.2h.i:
Hence show that , .
-
SPM.3.AHL.TZ0.2h.ii:
Hence express as a cubic polynomial.
-
18N.1.AHL.TZ0.H_3a:
For , sketch the graph of . Indicate clearly the maximum and minimum values of the function.
-
18N.1.AHL.TZ0.H_3b:
Write down the least value of such that has an inverse.
-
18N.1.AHL.TZ0.H_3c.i:
For the value of found in part (b), write down the domain of .
-
18N.1.AHL.TZ0.H_3c.ii:
For the value of found in part (b), find an expression for .
-
16N.2.AHL.TZ0.H_5a:
Sketch the graph of indicating clearly any intercepts with the axes and the coordinates of any local maximum or minimum points.
-
16N.2.AHL.TZ0.H_5b:
State the range of .
-
16N.2.AHL.TZ0.H_5c:
Solve the inequality .
-
17M.1.AHL.TZ1.H_3:
Solve the equation .
-
18N.1.AHL.TZ0.H_10a:
Use integration by parts to show that , .
-
18N.1.AHL.TZ0.H_10b:
Hence, show that , .
-
18N.1.AHL.TZ0.H_10c:
Find the -coordinates of A and of C , giving your answers in the form , where , .
-
18N.1.AHL.TZ0.H_10d:
Find the area enclosed by the curve and the -axis between B and D, as shaded on the diagram.
-
EXN.1.AHL.TZ0.12e:
Deduce a quadratic equation with integer coefficients, having roots and .
-
21M.1.AHL.TZ1.6:
It is given that , where . Find the exact value of .
-
21M.2.AHL.TZ1.9a:
Show that .
-
21M.1.AHL.TZ2.12b:
Show that where and .
-
21M.1.AHL.TZ2.12c:
Verify that for .
-
21M.2.AHL.TZ2.12a:
Show that is an even function.
-
21M.2.AHL.TZ2.12b:
By considering limits, show that the graph of has a horizontal asymptote and state its equation.
-
21M.2.AHL.TZ2.12c.i:
Show that for .
-
21M.2.AHL.TZ2.12c.ii:
By using the expression for and the result , show that is decreasing for .
-
21M.2.AHL.TZ2.12d:
Find an expression for , justifying your answer.
-
21M.2.AHL.TZ2.12e:
State the domain of .
-
21M.2.AHL.TZ2.12f:
Sketch the graph of , clearly indicating any asymptotes with their equations and stating the values of any axes intercepts.
-
21N.2.AHL.TZ0.7a:
Determine the value of .
-
21N.2.AHL.TZ0.7b:
Given that , determine the value of .
-
22M.1.AHL.TZ2.7:
By using the substitution or otherwise, find an expression for in terms of , where is a non-zero real number.
-
22M.1.AHL.TZ2.11c:
Given that , find the value of .
Give your answer in the form , where .
-
22M.2.AHL.TZ2.7a:
Show that a finite limit only exists for .
-
22M.2.AHL.TZ2.7b:
Using l’Hôpital’s rule, show algebraically that the value of the limit is .
AHL 3.10—Compound angle identities
-
SPM.2.AHL.TZ0.12a:
Show that .
-
SPM.2.AHL.TZ0.12b:
Verify that and satisfy the equation .
-
SPM.2.AHL.TZ0.12c:
Hence, or otherwise, show that the exact value of .
-
SPM.2.AHL.TZ0.12d:
Using the results from parts (b) and (c) find the exact value of .
Give your answer in the form where , .
-
EXM.3.AHL.TZ0.5a.i:
Sketch the graph , for
-
EXM.3.AHL.TZ0.5a.ii:
Write down the amplitude of this graph
-
EXM.3.AHL.TZ0.5a.iii:
Write down the period of this graph
-
EXM.3.AHL.TZ0.5b.i:
Use your answers from part (a) to write down the value of , and .
-
EXM.3.AHL.TZ0.5b.ii:
Find the value of .
-
EXM.3.AHL.TZ0.5c.i:
Find , giving the answer to 3 significant figures.
-
EXM.3.AHL.TZ0.5c.ii:
Comment on your answer to part (c)(i).
-
EXM.3.AHL.TZ0.5d:
By considering the graph of , find the value of , , and .
-
EXM.3.AHL.TZ0.5e.i:
.
-
EXM.3.AHL.TZ0.5e.ii:
.
-
EXM.3.AHL.TZ0.5e.iii:
.
-
EXM.3.AHL.TZ0.5e.iv:
.
-
EXM.3.AHL.TZ0.5f.i:
Show that .
-
EXM.3.AHL.TZ0.5f.ii:
Show that .
-
EXM.3.AHL.TZ0.5g:
Hence prove your conjectures in part (e).
-
18N.2.AHL.TZ0.H_11a:
Find an expression for in terms of .
-
18N.2.AHL.TZ0.H_11b:
Show that .
-
18N.2.AHL.TZ0.H_11c:
By sketching the graph of as a function of , determine the range of values of for which there are possible values of .
-
16N.1.AHL.TZ0.H_13a:
Find the value of .
-
16N.1.AHL.TZ0.H_13d:
Hence or otherwise solve the equation in the interval .
-
18N.1.AHL.TZ0.H_11a:
Find the roots of which satisfy the condition , expressing your answers in the form , where , .
-
18N.1.AHL.TZ0.H_11b.i:
Show that Re S = Im S.
-
18N.1.AHL.TZ0.H_11b.ii:
By writing as , find the value of cos in the form , where , and are integers to be determined.
-
18N.1.AHL.TZ0.H_11b.iii:
Hence, or otherwise, show that S = .
-
17M.1.AHL.TZ2.H_11a:
Solve .
-
17M.1.AHL.TZ2.H_11b:
Show that .
-
17M.1.AHL.TZ2.H_11c.i:
Find the modulus and argument of in terms of . Express each answer in its simplest form.
-
17M.1.AHL.TZ2.H_11c.ii:
Hence find the cube roots of in modulus-argument form.
-
19M.1.AHL.TZ1.H_9a:
Show that .
-
19M.1.AHL.TZ1.H_9b:
Show that .
-
19M.1.AHL.TZ1.H_9c:
Hence or otherwise find in the form where , .
-
18M.2.AHL.TZ1.H_3:
Let where .
Express in terms of sin and cos .
-
19N.1.AHL.TZ0.H_4:
and are acute angles such that and .
Show that .
-
EXN.1.AHL.TZ0.7:
Consider quadrilateral where is parallel to .
In , , , and .
Find an expression for in terms of and .
-
21M.1.AHL.TZ2.12b:
Show that where and .
-
21M.1.AHL.TZ2.12c:
Verify that for .
AHL 3.11—Relationships between trig functions
-
19M.2.AHL.TZ2.H_3a:
Complete the given probability tree diagram for Iqbal’s three attempts, labelling each branch with the correct probability.
-
19M.2.AHL.TZ2.H_3b:
Calculate the probability that Iqbal passes at least two of the papers he attempts.
-
19M.2.AHL.TZ2.H_3c:
Find the probability that Iqbal passes his third paper, given that he passed only one previous paper.
AHL 3.12—Vector definitions
-
19M.1.AHL.TZ1.H_11a.i:
Find how many sets of four points can be selected which can form the vertices of a quadrilateral.
-
19M.1.AHL.TZ1.H_11a.ii:
Find how many sets of three points can be selected which can form the vertices of a triangle.
-
19M.1.AHL.TZ1.H_11b:
Verify that is the point of intersection of the two lines.
-
19M.1.AHL.TZ1.H_11c:
Write down the value of corresponding to the point .
-
19M.1.AHL.TZ1.H_11d:
Write down and .
-
19M.1.AHL.TZ1.H_11e:
Let be the point on with coordinates (1, 0, 1) and be the point on with parameter .
Find the area of the quadrilateral .
-
17N.1.AHL.TZ0.H_9a.i:
Find, in terms of a and b .
-
17N.1.AHL.TZ0.H_9a.ii:
Find, in terms of a and b .
-
17N.1.AHL.TZ0.H_9b.i:
Find an expression for in terms of a, b and ;
-
17N.1.AHL.TZ0.H_9b.ii:
Find an expression for in terms of a, b and .
-
17N.1.AHL.TZ0.H_9c:
Show that , and find the value of .
-
17N.1.AHL.TZ0.H_9d:
Deduce an expression for in terms of a and b only.
-
17N.1.AHL.TZ0.H_9e:
Given that area , find the value of .
-
18M.2.AHL.TZ1.H_11a:
Show that the two submarines would collide at a point P and write down the coordinates of P.
-
18M.2.AHL.TZ1.H_11b.i:
Show that submarine B travels in the same direction as originally planned.
-
18M.2.AHL.TZ1.H_11b.ii:
Find the value of t when submarine B passes through P.
-
18M.2.AHL.TZ1.H_11c.i:
Find an expression for the distance between the two submarines in terms of t.
-
18M.2.AHL.TZ1.H_11c.ii:
Find the value of t when the two submarines are closest together.
-
18M.2.AHL.TZ1.H_11c.iii:
Find the distance between the two submarines at this time.
-
18M.1.AHL.TZ2.H_9a.i:
Explain why ABCD is a parallelogram.
-
18M.1.AHL.TZ2.H_9a.ii:
Using vector algebra, show that .
-
18M.1.AHL.TZ2.H_9b:
Show that p = 1, q = 1 and r = 4.
-
18M.1.AHL.TZ2.H_9c:
Find the area of the parallelogram ABCD.
-
18M.1.AHL.TZ2.H_9d:
Find the vector equation of the straight line passing through M and normal to the plane containing ABCD.
-
18M.1.AHL.TZ2.H_9e:
Find the Cartesian equation of .
-
18M.1.AHL.TZ2.H_9f.i:
Find the coordinates of X, Y and Z.
-
18M.1.AHL.TZ2.H_9f.ii:
Find YZ.
-
19M.1.AHL.TZ2.H_2a.i:
Find the vector .
-
19M.1.AHL.TZ2.H_2a.ii:
Find the vector .
-
19M.1.AHL.TZ2.H_2b:
Hence or otherwise, find the area of the triangle ABC.
-
18N.2.SL.TZ0.S_8a.i:
Find .
-
18N.2.SL.TZ0.S_8a.ii:
Find .
-
18N.2.SL.TZ0.S_8b.i:
Find the value of .
-
18N.2.SL.TZ0.S_8b.ii:
Show that .
-
18N.2.SL.TZ0.S_8c:
Find the angle between and .
-
18N.2.SL.TZ0.S_8d:
Find the area of triangle ABC.
-
17N.2.SL.TZ0.S_3a:
Find .
-
17N.2.SL.TZ0.S_3b:
Let . Find .
-
18M.1.SL.TZ1.S_9a:
Show that
-
18M.1.SL.TZ1.S_9b.i:
Find a vector equation for L.
-
18M.1.SL.TZ1.S_9b.ii:
Point C (k , 12 , −k) is on L. Show that k = 14.
-
18M.1.SL.TZ1.S_9c.i:
Find .
-
18M.1.SL.TZ1.S_9c.ii:
Write down the value of angle OBA.
-
18M.1.SL.TZ1.S_9d:
Point D is also on L and has coordinates (8, 4, −9).
Find the area of triangle OCD.
-
17M.1.SL.TZ1.S_8a.i:
Find .
-
17M.1.SL.TZ1.S_8a.ii:
Hence, write down a vector equation for .
-
17M.1.SL.TZ1.S_8b:
A second line , has equation r = .
Given that and are perpendicular, show that .
-
17M.1.SL.TZ1.S_8c:
The lines and intersect at . Find .
-
17M.1.SL.TZ1.S_8d.i:
Find a unit vector in the direction of .
-
17M.1.SL.TZ1.S_8d.ii:
Hence or otherwise, find one point on which is units from C.
-
19M.1.SL.TZ2.S_2a:
parallel.
-
19M.1.SL.TZ2.S_2b:
perpendicular.
-
19N.1.SL.TZ0.S_9a.i:
.
-
19N.1.SL.TZ0.S_9a.ii:
.
-
19N.1.SL.TZ0.S_9b:
Given that , show that .
-
19N.1.SL.TZ0.S_9c:
Calculate the area of triangle .
-
19N.2.SL.TZ0.S_2a:
Find the point of intersection of and .
-
19N.2.SL.TZ0.S_2b:
Write down a direction vector for .
-
19N.2.SL.TZ0.S_2c:
passes through the intersection of and .
Write down a vector equation for .
-
20N.1.SL.TZ0.S_9a:
Express in terms of .
-
20N.1.SL.TZ0.S_9b:
Find the value of .
-
20N.1.SL.TZ0.S_9c:
Consider a unit vector , such that , where .
Point is such that .
Find the coordinates of .
-
EXN.2.AHL.TZ0.11a:
Find the vectors and .
-
EXN.2.AHL.TZ0.11b:
Use a vector method to show that .
-
EXN.2.AHL.TZ0.11c:
Show that the Cartesian equation of the plane that contains the triangle is .
-
EXN.2.AHL.TZ0.11d.i:
Find a vector equation of the line .
-
EXN.2.AHL.TZ0.11d.ii:
Hence determine the minimum distance, , from to .
-
EXN.2.AHL.TZ0.11e:
Find the volume of right-pyramid .
-
21N.2.AHL.TZ0.11a.i:
Find the vector and the vector .
-
21N.2.AHL.TZ0.11a.ii:
Hence find the equation of , expressing your answer in the form , where .
-
21N.2.AHL.TZ0.11b:
The line is the intersection of and . Verify that the vector equation of can be written as .
-
21N.2.AHL.TZ0.11c.i:
Show that at the point .
-
21N.2.AHL.TZ0.11c.ii:
Hence find the coordinates of .
-
21N.2.AHL.TZ0.11d.i:
Find the reflection of the point in the plane .
-
21N.2.AHL.TZ0.11d.ii:
Hence find the vector equation of the line formed when is reflected in the plane .
-
22M.2.AHL.TZ1.7a:
Find the possible range of values for .
-
22M.2.AHL.TZ1.7b:
Given that is a minimum, find .
-
22M.2.AHL.TZ2.11b:
Show that airplane travels at a greater speed than airplane .
AHL 3.13—Scalar (dot) product
-
17M.1.AHL.TZ1.H_5a:
Find the area of the parallelogram ABCD.
-
17M.1.AHL.TZ1.H_5b:
By using a suitable scalar product of two vectors, determine whether is acute or obtuse.
-
18M.1.AHL.TZ2.H_1:
The acute angle between the vectors 3i − 4j − 5k and 5i − 4j + 3k is denoted by θ.
Find cos θ.
-
17M.2.AHL.TZ2.H_9a:
Find the vector equation of the line (BC).
-
17M.2.AHL.TZ2.H_9b:
Determine whether or not the lines (OA) and (BC) intersect.
-
17M.2.AHL.TZ2.H_9c:
Find the Cartesian equation of the plane Π, which passes through C and is perpendicular to .
-
17M.2.AHL.TZ2.H_9d:
Show that the line (BC) lies in the plane Π.
-
17M.2.AHL.TZ2.H_9e:
Verify that 2j + k is perpendicular to the plane Π.
-
17M.2.AHL.TZ2.H_9f:
Find a vector perpendicular to the plane Π.
-
17M.2.AHL.TZ2.H_9g:
Find the acute angle between the planes Π and Π.
-
18N.1.AHL.TZ0.H_5a:
Find and simplify an expression for a • b in terms of .
-
18N.1.AHL.TZ0.H_5b:
Hence or otherwise, find the values of for which the angle between a and b is obtuse .
-
19M.1.AHL.TZ1.H_1:
Let a = and b = , .
Given that a and b are perpendicular, find the possible values of .
-
18N.1.SL.TZ0.S_5:
Consider the vectors a = and b = .
Find the possible values of p for which a and b are parallel.
-
18M.1.SL.TZ1.S_6:
Six equilateral triangles, each with side length 3 cm, are arranged to form a hexagon.
This is shown in the following diagram.The vectors p , q and r are shown on the diagram.
Find p•(p + q + r).
-
19M.1.SL.TZ1.S_6:
The magnitudes of two vectors, u and v, are 4 and respectively. The angle between u and v is .
Let w = u − v. Find the magnitude of w.
-
18M.2.SL.TZ2.S_8a.i:
Find .
-
18M.2.SL.TZ2.S_8a.ii:
Find .
-
18M.2.SL.TZ2.S_8b:
Find the angle between PQ and PR.
-
18M.2.SL.TZ2.S_8c:
Find the area of triangle PQR.
-
18M.2.SL.TZ2.S_8d:
Hence or otherwise find the shortest distance from R to the line through P and Q.
-
18N.2.SL.TZ0.S_8a.i:
Find .
-
18N.2.SL.TZ0.S_8a.ii:
Find .
-
18N.2.SL.TZ0.S_8b.i:
Find the value of .
-
18N.2.SL.TZ0.S_8b.ii:
Show that .
-
18N.2.SL.TZ0.S_8c:
Find the angle between and .
-
18N.2.SL.TZ0.S_8d:
Find the area of triangle ABC.
-
17N.2.SL.TZ0.S_3a:
Find .
-
17N.2.SL.TZ0.S_3b:
Let . Find .
-
17N.1.SL.TZ0.S_9a.i:
Show that .
-
17N.1.SL.TZ0.S_9a.ii:
Find a vector equation for .
-
17N.1.SL.TZ0.S_9b:
Find the value of .
-
17N.1.SL.TZ0.S_9c:
The point D has coordinates . Given that is perpendicular to , find the possible values of .
-
18M.1.SL.TZ1.S_9a:
Show that
-
18M.1.SL.TZ1.S_9b.i:
Find a vector equation for L.
-
18M.1.SL.TZ1.S_9b.ii:
Point C (k , 12 , −k) is on L. Show that k = 14.
-
18M.1.SL.TZ1.S_9c.i:
Find .
-
18M.1.SL.TZ1.S_9c.ii:
Write down the value of angle OBA.
-
18M.1.SL.TZ1.S_9d:
Point D is also on L and has coordinates (8, 4, −9).
Find the area of triangle OCD.
-
17M.1.SL.TZ2.S_2a:
Find the value of .
-
17M.1.SL.TZ2.S_2b:
Given that c = a + 2b, find c.
-
17M.1.SL.TZ1.S_8a.i:
Find .
-
17M.1.SL.TZ1.S_8a.ii:
Hence, write down a vector equation for .
-
17M.1.SL.TZ1.S_8b:
A second line , has equation r = .
Given that and are perpendicular, show that .
-
17M.1.SL.TZ1.S_8c:
The lines and intersect at . Find .
-
17M.1.SL.TZ1.S_8d.i:
Find a unit vector in the direction of .
-
17M.1.SL.TZ1.S_8d.ii:
Hence or otherwise, find one point on which is units from C.
-
19M.1.SL.TZ2.S_2a:
parallel.
-
19M.1.SL.TZ2.S_2b:
perpendicular.
-
19M.2.SL.TZ2.S_7:
The vector equation of line is given by r .
Point P is the point on that is closest to the origin. Find the coordinates of P.
-
18M.1.SL.TZ2.S_1a:
Find a vector equation for L1.
-
18M.1.SL.TZ2.S_1b:
The vector is perpendicular to . Find the value of p.
-
16N.1.SL.TZ0.S_4a:
Find a vector equation of the line that passes through P and Q.
-
16N.1.SL.TZ0.S_4b:
The line through P and Q is perpendicular to the vector 2i nk. Find the value of .
-
19N.1.SL.TZ0.S_9a.i:
.
-
19N.1.SL.TZ0.S_9a.ii:
.
-
19N.1.SL.TZ0.S_9b:
Given that , show that .
-
19N.1.SL.TZ0.S_9c:
Calculate the area of triangle .
-
EXN.1.AHL.TZ0.8a:
Show that and are never perpendicular to each other.
-
EXN.2.AHL.TZ0.11a:
Find the vectors and .
-
EXN.2.AHL.TZ0.11b:
Use a vector method to show that .
-
EXN.2.AHL.TZ0.11c:
Show that the Cartesian equation of the plane that contains the triangle is .
-
EXN.2.AHL.TZ0.11d.i:
Find a vector equation of the line .
-
EXN.2.AHL.TZ0.11d.ii:
Hence determine the minimum distance, , from to .
-
EXN.2.AHL.TZ0.11e:
Find the volume of right-pyramid .
-
21M.1.AHL.TZ2.5:
Given any two non-zero vectors, and , show that .
-
21M.1.AHL.TZ2.8a:
Show that and do not intersect.
-
21M.1.AHL.TZ2.8b:
Find the minimum distance between and .
-
21N.2.AHL.TZ0.11a.i:
Find the vector and the vector .
-
21N.2.AHL.TZ0.11a.ii:
Hence find the equation of , expressing your answer in the form , where .
-
21N.2.AHL.TZ0.11b:
The line is the intersection of and . Verify that the vector equation of can be written as .
-
21N.2.AHL.TZ0.11c.i:
Show that at the point .
-
21N.2.AHL.TZ0.11c.ii:
Hence find the coordinates of .
-
21N.2.AHL.TZ0.11d.i:
Find the reflection of the point in the plane .
-
21N.2.AHL.TZ0.11d.ii:
Hence find the vector equation of the line formed when is reflected in the plane .
-
22M.2.AHL.TZ1.7c:
Find such that and is perpendicular to .
-
22M.2.AHL.TZ2.11c:
Find the acute angle between the two airplanes’ lines of flight. Give your answer in degrees.
-
22M.2.AHL.TZ2.11e:
Let represent the distance between airplane and airplane for .
Find the minimum value of .
AHL 3.14—Vector equation of line
-
SPM.1.AHL.TZ0.8:
The plane П has the Cartesian equation
The line L has the vector equation r . The acute angle between the line L and the plane П is 30°.
Find the possible values of .
-
SPM.2.AHL.TZ0.7:
Two ships, A and B , are observed from an origin O. Relative to O, their position vectors at time t hours after midday are given by
rA =
rB =
where distances are measured in kilometres.
Find the minimum distance between the two ships.
-
19M.1.AHL.TZ1.H_11a.i:
Find how many sets of four points can be selected which can form the vertices of a quadrilateral.
-
19M.1.AHL.TZ1.H_11a.ii:
Find how many sets of three points can be selected which can form the vertices of a triangle.
-
19M.1.AHL.TZ1.H_11b:
Verify that is the point of intersection of the two lines.
-
19M.1.AHL.TZ1.H_11c:
Write down the value of corresponding to the point .
-
19M.1.AHL.TZ1.H_11d:
Write down and .
-
19M.1.AHL.TZ1.H_11e:
Let be the point on with coordinates (1, 0, 1) and be the point on with parameter .
Find the area of the quadrilateral .
-
18M.1.AHL.TZ2.H_9a.i:
Explain why ABCD is a parallelogram.
-
18M.1.AHL.TZ2.H_9a.ii:
Using vector algebra, show that .
-
18M.1.AHL.TZ2.H_9b:
Show that p = 1, q = 1 and r = 4.
-
18M.1.AHL.TZ2.H_9c:
Find the area of the parallelogram ABCD.
-
18M.1.AHL.TZ2.H_9d:
Find the vector equation of the straight line passing through M and normal to the plane containing ABCD.
-
18M.1.AHL.TZ2.H_9e:
Find the Cartesian equation of .
-
18M.1.AHL.TZ2.H_9f.i:
Find the coordinates of X, Y and Z.
-
18M.1.AHL.TZ2.H_9f.ii:
Find YZ.
-
17M.2.AHL.TZ2.H_9a:
Find the vector equation of the line (BC).
-
17M.2.AHL.TZ2.H_9b:
Determine whether or not the lines (OA) and (BC) intersect.
-
17M.2.AHL.TZ2.H_9c:
Find the Cartesian equation of the plane Π, which passes through C and is perpendicular to .
-
17M.2.AHL.TZ2.H_9d:
Show that the line (BC) lies in the plane Π.
-
17M.2.AHL.TZ2.H_9e:
Verify that 2j + k is perpendicular to the plane Π.
-
17M.2.AHL.TZ2.H_9f:
Find a vector perpendicular to the plane Π.
-
17M.2.AHL.TZ2.H_9g:
Find the acute angle between the planes Π and Π.
-
17N.1.AHL.TZ0.H_2a:
Find a vector equation of the line L passing through the points A and B.
-
17N.1.AHL.TZ0.H_2b:
Find the coordinates of the point of intersection of the line L with the plane Π.
-
18N.1.AHL.TZ0.H_9a:
Find, in terms of , a Cartesian equation of the plane Π containing this triangle.
-
18N.1.AHL.TZ0.H_9b:
Find, in terms of , the equation of the line L which passes through M and is perpendicular to the plane П.
-
18N.1.AHL.TZ0.H_9c:
Show that L does not intersect the -axis for any negative value of .
-
16N.1.AHL.TZ0.H_8a:
find the value of ;
-
16N.1.AHL.TZ0.H_8b:
determine the coordinates of the point of intersection P.
-
19M.2.SL.TZ1.S_9a:
Find the gradient of .
-
17M.1.SL.TZ2.S_9a:
Find the coordinates of A.
-
17M.1.SL.TZ2.S_9b.i:
Find ;
-
17M.1.SL.TZ2.S_9b.ii:
Find .
-
17M.1.SL.TZ2.S_9c:
Find .
-
17M.1.SL.TZ2.S_9d:
Hence or otherwise, find the distance between and two seconds after they leave A.
-
18N.2.SL.TZ0.S_8a.i:
Find .
-
18N.2.SL.TZ0.S_8a.ii:
Find .
-
18N.2.SL.TZ0.S_8b.i:
Find the value of .
-
18N.2.SL.TZ0.S_8b.ii:
Show that .
-
18N.2.SL.TZ0.S_8c:
Find the angle between and .
-
18N.2.SL.TZ0.S_8d:
Find the area of triangle ABC.
-
17N.1.SL.TZ0.S_9a.i:
Show that .
-
17N.1.SL.TZ0.S_9a.ii:
Find a vector equation for .
-
17N.1.SL.TZ0.S_9b:
Find the value of .
-
17N.1.SL.TZ0.S_9c:
The point D has coordinates . Given that is perpendicular to , find the possible values of .
-
18M.1.SL.TZ1.S_9a:
Show that
-
18M.1.SL.TZ1.S_9b.i:
Find a vector equation for L.
-
18M.1.SL.TZ1.S_9b.ii:
Point C (k , 12 , −k) is on L. Show that k = 14.
-
18M.1.SL.TZ1.S_9c.i:
Find .
-
18M.1.SL.TZ1.S_9c.ii:
Write down the value of angle OBA.
-
18M.1.SL.TZ1.S_9d:
Point D is also on L and has coordinates (8, 4, −9).
Find the area of triangle OCD.
-
17M.1.SL.TZ1.S_8a.i:
Find .
-
17M.1.SL.TZ1.S_8a.ii:
Hence, write down a vector equation for .
-
17M.1.SL.TZ1.S_8b:
A second line , has equation r = .
Given that and are perpendicular, show that .
-
17M.1.SL.TZ1.S_8c:
The lines and intersect at . Find .
-
17M.1.SL.TZ1.S_8d.i:
Find a unit vector in the direction of .
-
17M.1.SL.TZ1.S_8d.ii:
Hence or otherwise, find one point on which is units from C.
-
19M.1.SL.TZ1.S_2a:
Find .
-
19M.1.SL.TZ1.S_2b:
A second line, , is parallel to and passes through (1, 2, 3).
Write down a vector equation for .
-
19M.2.SL.TZ2.S_7:
The vector equation of line is given by r .
Point P is the point on that is closest to the origin. Find the coordinates of P.
-
18M.1.SL.TZ2.S_1a:
Find a vector equation for L1.
-
18M.1.SL.TZ2.S_1b:
The vector is perpendicular to . Find the value of p.
-
16N.1.SL.TZ0.S_4a:
Find a vector equation of the line that passes through P and Q.
-
16N.1.SL.TZ0.S_4b:
The line through P and Q is perpendicular to the vector 2i nk. Find the value of .
-
19N.1.AHL.TZ0.H_8:
A straight line, , has vector equation r .
The plane , has equation .
Show that the angle between and is independent of both and .
-
19N.2.SL.TZ0.S_2a:
Find the point of intersection of and .
-
19N.2.SL.TZ0.S_2b:
Write down a direction vector for .
-
19N.2.SL.TZ0.S_2c:
passes through the intersection of and .
Write down a vector equation for .
-
20N.1.SL.TZ0.S_7a:
Find an expression for the velocity of at time .
-
20N.1.SL.TZ0.S_7b:
Particle also moves in a straight line. The position of is given by .
The speed of is greater than the speed of when .
Find the value of .
-
20N.1.SL.TZ0.S_9a:
Express in terms of .
-
20N.1.SL.TZ0.S_9b:
Find the value of .
-
20N.1.SL.TZ0.S_9c:
Consider a unit vector , such that , where .
Point is such that .
Find the coordinates of .
-
EXN.1.AHL.TZ0.8a:
Show that and are never perpendicular to each other.
-
EXN.2.AHL.TZ0.11a:
Find the vectors and .
-
EXN.2.AHL.TZ0.11b:
Use a vector method to show that .
-
EXN.2.AHL.TZ0.11c:
Show that the Cartesian equation of the plane that contains the triangle is .
-
EXN.2.AHL.TZ0.11d.i:
Find a vector equation of the line .
-
EXN.2.AHL.TZ0.11d.ii:
Hence determine the minimum distance, , from to .
-
EXN.2.AHL.TZ0.11e:
Find the volume of right-pyramid .
-
21M.1.AHL.TZ1.11a.i:
Show that the point lies on .
-
21M.1.AHL.TZ1.11a.ii:
Find a vector equation of .
-
21M.1.AHL.TZ1.11b:
Find the possible values of when the acute angle between and is .
-
21M.1.AHL.TZ1.11c:
It is given that the lines and have a unique point of intersection, , when .
Find the value of , and find the coordinates of the point in terms of .
-
21M.1.AHL.TZ2.8a:
Show that and do not intersect.
-
21M.1.AHL.TZ2.8b:
Find the minimum distance between and .
-
21N.2.AHL.TZ0.11a.i:
Find the vector and the vector .
-
21N.2.AHL.TZ0.11a.ii:
Hence find the equation of , expressing your answer in the form , where .
-
21N.2.AHL.TZ0.11b:
The line is the intersection of and . Verify that the vector equation of can be written as .
-
21N.2.AHL.TZ0.11c.i:
Show that at the point .
-
21N.2.AHL.TZ0.11c.ii:
Hence find the coordinates of .
-
21N.2.AHL.TZ0.11d.i:
Find the reflection of the point in the plane .
-
21N.2.AHL.TZ0.11d.ii:
Hence find the vector equation of the line formed when is reflected in the plane .
-
22M.1.AHL.TZ1.11a:
Show that the three planes do not intersect.
-
22M.1.AHL.TZ1.11b.i:
Verify that the point lies on both and .
-
22M.1.AHL.TZ1.11b.ii:
Find a vector equation of , the line of intersection of and .
-
22M.1.AHL.TZ1.11c:
Find the distance between and .
-
22M.2.AHL.TZ2.11b:
Show that airplane travels at a greater speed than airplane .
AHL 3.15—Classification of lines
-
18M.2.AHL.TZ1.H_11a:
Show that the two submarines would collide at a point P and write down the coordinates of P.
-
18M.2.AHL.TZ1.H_11b.i:
Show that submarine B travels in the same direction as originally planned.
-
18M.2.AHL.TZ1.H_11b.ii:
Find the value of t when submarine B passes through P.
-
18M.2.AHL.TZ1.H_11c.i:
Find an expression for the distance between the two submarines in terms of t.
-
18M.2.AHL.TZ1.H_11c.ii:
Find the value of t when the two submarines are closest together.
-
18M.2.AHL.TZ1.H_11c.iii:
Find the distance between the two submarines at this time.
-
17M.2.AHL.TZ2.H_9a:
Find the vector equation of the line (BC).
-
17M.2.AHL.TZ2.H_9b:
Determine whether or not the lines (OA) and (BC) intersect.
-
17M.2.AHL.TZ2.H_9c:
Find the Cartesian equation of the plane Π, which passes through C and is perpendicular to .
-
17M.2.AHL.TZ2.H_9d:
Show that the line (BC) lies in the plane Π.
-
17M.2.AHL.TZ2.H_9e:
Verify that 2j + k is perpendicular to the plane Π.
-
17M.2.AHL.TZ2.H_9f:
Find a vector perpendicular to the plane Π.
-
17M.2.AHL.TZ2.H_9g:
Find the acute angle between the planes Π and Π.
-
17M.1.SL.TZ1.S_8a.i:
Find .
-
17M.1.SL.TZ1.S_8a.ii:
Hence, write down a vector equation for .
-
17M.1.SL.TZ1.S_8b:
A second line , has equation r = .
Given that and are perpendicular, show that .
-
17M.1.SL.TZ1.S_8c:
The lines and intersect at . Find .
-
17M.1.SL.TZ1.S_8d.i:
Find a unit vector in the direction of .
-
17M.1.SL.TZ1.S_8d.ii:
Hence or otherwise, find one point on which is units from C.
-
21M.1.AHL.TZ1.11a.i:
Show that the point lies on .
-
21M.1.AHL.TZ1.11a.ii:
Find a vector equation of .
-
21M.1.AHL.TZ1.11b:
Find the possible values of when the acute angle between and is .
-
21M.1.AHL.TZ1.11c:
It is given that the lines and have a unique point of intersection, , when .
Find the value of , and find the coordinates of the point in terms of .
-
21M.1.AHL.TZ2.8a:
Show that and do not intersect.
-
21M.1.AHL.TZ2.8b:
Find the minimum distance between and .
-
22M.1.AHL.TZ1.11a:
Show that the three planes do not intersect.
-
22M.1.AHL.TZ1.11b.i:
Verify that the point lies on both and .
-
22M.1.AHL.TZ1.11b.ii:
Find a vector equation of , the line of intersection of and .
-
22M.1.AHL.TZ1.11c:
Find the distance between and .
-
22M.2.AHL.TZ2.11d.i:
Find the coordinates of .
-
22M.2.AHL.TZ2.11d.ii:
Determine the length of time between the first airplane arriving at and the second airplane arriving at .
AHL 3.16—Vector product
-
19M.1.AHL.TZ1.H_11a.i:
Find how many sets of four points can be selected which can form the vertices of a quadrilateral.
-
19M.1.AHL.TZ1.H_11a.ii:
Find how many sets of three points can be selected which can form the vertices of a triangle.
-
19M.1.AHL.TZ1.H_11b:
Verify that is the point of intersection of the two lines.
-
19M.1.AHL.TZ1.H_11c:
Write down the value of corresponding to the point .
-
19M.1.AHL.TZ1.H_11d:
Write down and .
-
19M.1.AHL.TZ1.H_11e:
Let be the point on with coordinates (1, 0, 1) and be the point on with parameter .
Find the area of the quadrilateral .
-
19M.1.AHL.TZ2.H_2a.i:
Find the vector .
-
19M.1.AHL.TZ2.H_2a.ii:
Find the vector .
-
19M.1.AHL.TZ2.H_2b:
Hence or otherwise, find the area of the triangle ABC.
-
17M.1.AHL.TZ1.H_5a:
Find the area of the parallelogram ABCD.
-
17M.1.AHL.TZ1.H_5b:
By using a suitable scalar product of two vectors, determine whether is acute or obtuse.
-
17M.2.AHL.TZ2.H_7:
Given that a b b c 0 prove that a c sb where s is a scalar.
-
16N.1.AHL.TZ0.H_4a:
Find a b.
-
16N.1.AHL.TZ0.H_4b:
Hence find the Cartesian equation of the plane containing the vectors a and b, and passing through the point .
-
19N.1.AHL.TZ0.H_11a.i:
Show that and find a similar expression for .
-
19N.1.AHL.TZ0.H_11a.ii:
Hence, show that, if the angle between the faces and is , then .
-
19N.1.SL.TZ0.S_9a.i:
.
-
19N.1.SL.TZ0.S_9a.ii:
.
-
19N.1.SL.TZ0.S_9b:
Given that , show that .
-
19N.1.SL.TZ0.S_9c:
Calculate the area of triangle .
-
20N.2.AHL.TZ0.H_10a:
Given that meets at the point , find the coordinates of .
-
20N.2.AHL.TZ0.H_10b:
Find the shortest distance from the point to .
-
20N.2.AHL.TZ0.H_10c:
Find the equation of , giving your answer in the form .
-
20N.2.AHL.TZ0.H_10d:
Determine the acute angle between and .
-
EXN.2.AHL.TZ0.11a:
Find the vectors and .
-
EXN.2.AHL.TZ0.11b:
Use a vector method to show that .
-
EXN.2.AHL.TZ0.11c:
Show that the Cartesian equation of the plane that contains the triangle is .
-
EXN.2.AHL.TZ0.11d.i:
Find a vector equation of the line .
-
EXN.2.AHL.TZ0.11d.ii:
Hence determine the minimum distance, , from to .
-
EXN.2.AHL.TZ0.11e:
Find the volume of right-pyramid .
-
21M.2.AHL.TZ1.6a:
Find a Cartesian equation of the plane which is perpendicular to and and passes through the origin .
-
21M.2.AHL.TZ1.6b:
Find the coordinates of the point where , and intersect.
-
21M.1.AHL.TZ2.5:
Given any two non-zero vectors, and , show that .
-
21M.1.AHL.TZ2.8a:
Show that and do not intersect.
-
21M.1.AHL.TZ2.8b:
Find the minimum distance between and .
-
21N.2.AHL.TZ0.11a.i:
Find the vector and the vector .
-
21N.2.AHL.TZ0.11a.ii:
Hence find the equation of , expressing your answer in the form , where .
-
21N.2.AHL.TZ0.11b:
The line is the intersection of and . Verify that the vector equation of can be written as .
-
21N.2.AHL.TZ0.11c.i:
Show that at the point .
-
21N.2.AHL.TZ0.11c.ii:
Hence find the coordinates of .
-
21N.2.AHL.TZ0.11d.i:
Find the reflection of the point in the plane .
-
21N.2.AHL.TZ0.11d.ii:
Hence find the vector equation of the line formed when is reflected in the plane .
-
22M.1.AHL.TZ1.11a:
Show that the three planes do not intersect.
-
22M.1.AHL.TZ1.11b.i:
Verify that the point lies on both and .
-
22M.1.AHL.TZ1.11b.ii:
Find a vector equation of , the line of intersection of and .
-
22M.1.AHL.TZ1.11c:
Find the distance between and .
AHL 3.17—Vector equations of a plane
-
18M.1.AHL.TZ2.H_9a.i:
Explain why ABCD is a parallelogram.
-
18M.1.AHL.TZ2.H_9a.ii:
Using vector algebra, show that .
-
18M.1.AHL.TZ2.H_9b:
Show that p = 1, q = 1 and r = 4.
-
18M.1.AHL.TZ2.H_9c:
Find the area of the parallelogram ABCD.
-
18M.1.AHL.TZ2.H_9d:
Find the vector equation of the straight line passing through M and normal to the plane containing ABCD.
-
18M.1.AHL.TZ2.H_9e:
Find the Cartesian equation of .
-
18M.1.AHL.TZ2.H_9f.i:
Find the coordinates of X, Y and Z.
-
18M.1.AHL.TZ2.H_9f.ii:
Find YZ.
-
17M.2.AHL.TZ2.H_9a:
Find the vector equation of the line (BC).
-
17M.2.AHL.TZ2.H_9b:
Determine whether or not the lines (OA) and (BC) intersect.
-
17M.2.AHL.TZ2.H_9c:
Find the Cartesian equation of the plane Π, which passes through C and is perpendicular to .
-
17M.2.AHL.TZ2.H_9d:
Show that the line (BC) lies in the plane Π.
-
17M.2.AHL.TZ2.H_9e:
Verify that 2j + k is perpendicular to the plane Π.
-
17M.2.AHL.TZ2.H_9f:
Find a vector perpendicular to the plane Π.
-
17M.2.AHL.TZ2.H_9g:
Find the acute angle between the planes Π and Π.
-
18N.1.AHL.TZ0.H_9a:
Find, in terms of , a Cartesian equation of the plane Π containing this triangle.
-
18N.1.AHL.TZ0.H_9b:
Find, in terms of , the equation of the line L which passes through M and is perpendicular to the plane П.
-
18N.1.AHL.TZ0.H_9c:
Show that L does not intersect the -axis for any negative value of .
-
16N.1.AHL.TZ0.H_4a:
Find a b.
-
16N.1.AHL.TZ0.H_4b:
Hence find the Cartesian equation of the plane containing the vectors a and b, and passing through the point .
-
17M.2.AHL.TZ1.H_7:
Find the Cartesian equation of plane Π containing the points and and perpendicular to the plane .
-
18M.1.AHL.TZ1.H_10a:
Find the Cartesian equation of the plane , passing through the points A , B and D.
-
18M.1.AHL.TZ1.H_10b:
Find the angle between the faces ABD and BCD.
-
18M.1.AHL.TZ1.H_10c:
Find the Cartesian equation of .
-
18M.1.AHL.TZ1.H_10d:
Show that P is the midpoint of AD.
-
18M.1.AHL.TZ1.H_10e:
Find the area of the triangle OPQ.
-
19M.2.AHL.TZ2.H_11a:
Find the Cartesian equation of the plane containing P, Q and R.
-
19M.2.AHL.TZ2.H_11b:
Given that П1 and П2 meet in a line , verify that the vector equation of can be given by r .
-
19M.2.AHL.TZ2.H_11c:
Given that П3 is parallel to the line , show that .
-
19M.2.AHL.TZ2.H_11d.i:
Show that .
-
19M.2.AHL.TZ2.H_11d.ii:
Given that П3 is equally inclined to both П1 and П2, determine two distinct possible Cartesian equations for П3.
-
EXN.1.AHL.TZ0.8b.i:
the value of .
-
EXN.1.AHL.TZ0.8b.ii:
the condition on the value of .
-
EXN.2.AHL.TZ0.11a:
Find the vectors and .
-
EXN.2.AHL.TZ0.11b:
Use a vector method to show that .
-
EXN.2.AHL.TZ0.11c:
Show that the Cartesian equation of the plane that contains the triangle is .
-
EXN.2.AHL.TZ0.11d.i:
Find a vector equation of the line .
-
EXN.2.AHL.TZ0.11d.ii:
Hence determine the minimum distance, , from to .
-
EXN.2.AHL.TZ0.11e:
Find the volume of right-pyramid .
-
21M.2.AHL.TZ1.6a:
Find a Cartesian equation of the plane which is perpendicular to and and passes through the origin .
-
21M.2.AHL.TZ1.6b:
Find the coordinates of the point where , and intersect.
-
21N.2.AHL.TZ0.11a.i:
Find the vector and the vector .
-
21N.2.AHL.TZ0.11a.ii:
Hence find the equation of , expressing your answer in the form , where .
-
21N.2.AHL.TZ0.11b:
The line is the intersection of and . Verify that the vector equation of can be written as .
-
21N.2.AHL.TZ0.11c.i:
Show that at the point .
-
21N.2.AHL.TZ0.11c.ii:
Hence find the coordinates of .
-
21N.2.AHL.TZ0.11d.i:
Find the reflection of the point in the plane .
-
21N.2.AHL.TZ0.11d.ii:
Hence find the vector equation of the line formed when is reflected in the plane .
-
22M.1.AHL.TZ1.11a:
Show that the three planes do not intersect.
-
22M.1.AHL.TZ1.11b.i:
Verify that the point lies on both and .
-
22M.1.AHL.TZ1.11b.ii:
Find a vector equation of , the line of intersection of and .
-
22M.1.AHL.TZ1.11c:
Find the distance between and .
AHL 3.18—Intersections of lines & planes
-
16N.2.AHL.TZ0.H_2:
Find the acute angle between the planes with equations and .
-
18M.1.AHL.TZ2.H_9a.i:
Explain why ABCD is a parallelogram.
-
18M.1.AHL.TZ2.H_9a.ii:
Using vector algebra, show that .
-
18M.1.AHL.TZ2.H_9b:
Show that p = 1, q = 1 and r = 4.
-
18M.1.AHL.TZ2.H_9c:
Find the area of the parallelogram ABCD.
-
18M.1.AHL.TZ2.H_9d:
Find the vector equation of the straight line passing through M and normal to the plane containing ABCD.
-
18M.1.AHL.TZ2.H_9e:
Find the Cartesian equation of .
-
18M.1.AHL.TZ2.H_9f.i:
Find the coordinates of X, Y and Z.
-
18M.1.AHL.TZ2.H_9f.ii:
Find YZ.
-
17N.1.AHL.TZ0.H_2a:
Find a vector equation of the line L passing through the points A and B.
-
17N.1.AHL.TZ0.H_2b:
Find the coordinates of the point of intersection of the line L with the plane Π.
-
18N.1.AHL.TZ0.H_9a:
Find, in terms of , a Cartesian equation of the plane Π containing this triangle.
-
18N.1.AHL.TZ0.H_9b:
Find, in terms of , the equation of the line L which passes through M and is perpendicular to the plane П.
-
18N.1.AHL.TZ0.H_9c:
Show that L does not intersect the -axis for any negative value of .
-
16N.1.AHL.TZ0.H_8a:
find the value of ;
-
16N.1.AHL.TZ0.H_8b:
determine the coordinates of the point of intersection P.
-
18M.1.AHL.TZ1.H_10a:
Find the Cartesian equation of the plane , passing through the points A , B and D.
-
18M.1.AHL.TZ1.H_10b:
Find the angle between the faces ABD and BCD.
-
18M.1.AHL.TZ1.H_10c:
Find the Cartesian equation of .
-
18M.1.AHL.TZ1.H_10d:
Show that P is the midpoint of AD.
-
18M.1.AHL.TZ1.H_10e:
Find the area of the triangle OPQ.
-
19M.2.AHL.TZ2.H_11a:
Find the Cartesian equation of the plane containing P, Q and R.
-
19M.2.AHL.TZ2.H_11b:
Given that П1 and П2 meet in a line , verify that the vector equation of can be given by r .
-
19M.2.AHL.TZ2.H_11c:
Given that П3 is parallel to the line , show that .
-
19M.2.AHL.TZ2.H_11d.i:
Show that .
-
19M.2.AHL.TZ2.H_11d.ii:
Given that П3 is equally inclined to both П1 and П2, determine two distinct possible Cartesian equations for П3.
-
16N.1.AHL.TZ0.H_1:
Find the coordinates of the point of intersection of the planes defined by the equations and .
-
19N.1.AHL.TZ0.H_11b.i:
Find the two possible coordinates of .
-
19N.1.AHL.TZ0.H_11b.ii:
Comment on the positions of in relation to the plane .
-
19N.1.AHL.TZ0.H_11c.i:
At , find the value of and the value of .
-
19N.1.AHL.TZ0.H_11c.ii:
Find the equation of the horizontal asymptote of the graph.
-
19N.1.AHL.TZ0.H_3:
Three planes have equations:
, where .
Find the set of values of and such that the three planes have no points of intersection.
-
19N.1.AHL.TZ0.H_8:
A straight line, , has vector equation r .
The plane , has equation .
Show that the angle between and is independent of both and .
-
20N.2.AHL.TZ0.H_10a:
Given that meets at the point , find the coordinates of .
-
20N.2.AHL.TZ0.H_10b:
Find the shortest distance from the point to .
-
20N.2.AHL.TZ0.H_10c:
Find the equation of , giving your answer in the form .
-
20N.2.AHL.TZ0.H_10d:
Determine the acute angle between and .
-
EXN.2.AHL.TZ0.11a:
Find the vectors and .
-
EXN.2.AHL.TZ0.11b:
Use a vector method to show that .
-
EXN.2.AHL.TZ0.11c:
Show that the Cartesian equation of the plane that contains the triangle is .
-
EXN.2.AHL.TZ0.11d.i:
Find a vector equation of the line .
-
EXN.2.AHL.TZ0.11d.ii:
Hence determine the minimum distance, , from to .
-
EXN.2.AHL.TZ0.11e:
Find the volume of right-pyramid .
-
21M.2.AHL.TZ1.6a:
Find a Cartesian equation of the plane which is perpendicular to and and passes through the origin .
-
21M.2.AHL.TZ1.6b:
Find the coordinates of the point where , and intersect.
-
21N.2.AHL.TZ0.11a.i:
Find the vector and the vector .
-
21N.2.AHL.TZ0.11a.ii:
Hence find the equation of , expressing your answer in the form , where .
-
21N.2.AHL.TZ0.11b:
The line is the intersection of and . Verify that the vector equation of can be written as .
-
21N.2.AHL.TZ0.11c.i:
Show that at the point .
-
21N.2.AHL.TZ0.11c.ii:
Hence find the coordinates of .
-
21N.2.AHL.TZ0.11d.i:
Find the reflection of the point in the plane .
-
21N.2.AHL.TZ0.11d.ii:
Hence find the vector equation of the line formed when is reflected in the plane .
-
22M.1.AHL.TZ1.11a:
Show that the three planes do not intersect.
-
22M.1.AHL.TZ1.11b.i:
Verify that the point lies on both and .
-
22M.1.AHL.TZ1.11b.ii:
Find a vector equation of , the line of intersection of and .
-
22M.1.AHL.TZ1.11c:
Find the distance between and .
