| Date | November 2020 | Marks available | 4 | Reference code | 20N.2.SL.TZ0.T_3 |
| Level | Standard Level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Show that | Question number | T_3 | Adapted from | N/A |
Question
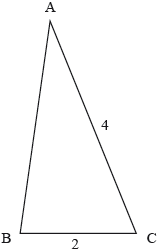
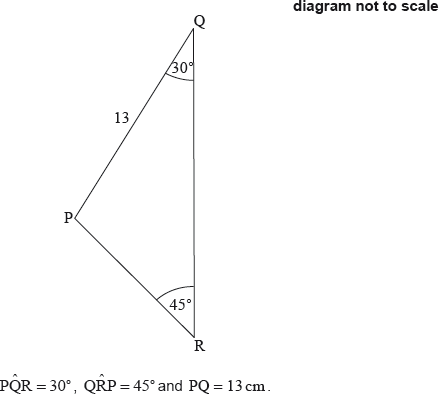
Using geometry software, Pedro draws a quadrilateral . and . Angle and angle . This information is shown in the diagram.
, where point is the midpoint of .
Calculate the length of .
Show that angle , correct to three significant figures.
Calculate the area of triangle .
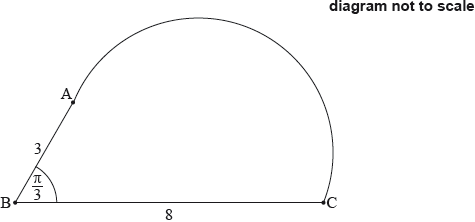
Pedro draws a circle, with centre at point , passing through point . Part of the circle is shown in the diagram.
Show that point lies outside this circle. Justify your reasoning.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(M1)(A1)
Note: Award (M1) for substituted sine rule, (A1) for correct substitution.
(A1)(G2)
Note: If radians are used the answer is award at most (M1)(A1)(A0).
[3 marks]
(A1)(ft)(M1)(A1)(ft)
Note: Award (A1) for or seen, (M1) for substituted cosine rule, (A1)(ft) for correct substitutions.
(A1)
( sig figures) (AG)
Note: Both an unrounded answer that rounds to the given answer and the rounded value must be seen for the final (M1) to be awarded.
Award at most (A1)(ft)(M1)(A1)(ft)(A0) if the known angle is used to validate the result. Follow through from their in part (a).
[4 marks]
Units are required in this question.
(M1)(A1)(ft)
Note: Award (M1) for substituted area formula. Award (A1) for correct substitution.
(A1)(ft)(G3)
Note: Follow through from part (a).
[3 marks]
(A1)(M1)(A1)(ft)
Note: Award (A1) for seen. Award (M1) for substituted cosine rule to find , (A1)(ft) for correct substitutions.
(A1)(ft)(G3)
Note: Follow through from part (a).
OR
(A1)(M1)(A1)(ft)
Note: Award (A1) for or seen. Award (M1) for substituted cosine rule to find (do not award (M1) for cosine or sine rule to find ), (A1)(ft) for correct substitutions.
(A1)(ft)(G3)
Note: Follow through from part (a).
. (A1)(ft)
point is outside the circle. (AG)
Note: Award (A1) for a numerical comparison of and . Follow through for the final (A1)(ft) within the part for their . The final (A1)(ft) is contingent on a valid method to find the value of .
Do not award the final (A1)(ft) if the (AG) line is not stated.
Do not award the final (A1)(ft) if their point is inside the circle.
[5 marks]