| Date | November 2017 | Marks available | 3 | Reference code | 17N.1.SL.TZ0.S_4 |
| Level | Standard Level | Paper | Paper 1 (without calculator) | Time zone | Time zone 0 |
| Command term | Find | Question number | S_4 | Adapted from | N/A |
Question
The following diagram shows triangle ABC, with , , and .
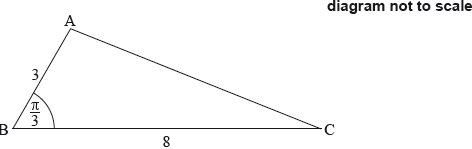
Show that .
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

Find the exact perimeter of this shape.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
evidence of choosing the cosine rule (M1)
eg
correct substitution into RHS of cosine rule (A1)
eg
evidence of correct value for (may be seen anywhere, including in cosine rule) A1
eg
correct working clearly leading to answer A1
eg
AG N0
Note: Award no marks if the only working seen is or (or similar).
[4 marks]
correct substitution for semicircle (A1)
eg
valid approach (seen anywhere) (M1)
eg
A1 N2
[3 marks]



