IB Questionbank

User interface language: English | Español

Date	May 2021	Marks available	2	Reference code	21M.2.SL.TZ2.7
Level	Standard Level	Paper	Paper 2	Time zone	Time zone 2
Command term	Find	Question number	7	Adapted from	N/A

Question

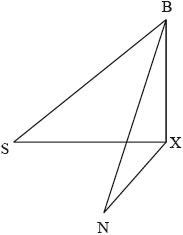
The six blades of a windmill rotate around a centre point $C$ . Points $A$ and $B$ and the base of the windmill are on level ground, as shown in the following diagram.

From point $A$ the angle of elevation of point $C$ is $0.6$ radians.

An observer walks $7$ metres from point $A$ to point $B$ .

The observer keeps walking until he is standing directly under point $C$ . The observer has a height of $1.8$ metres, and as the blades of the windmill rotate, the end of each blade passes $2.5$ metres over his head.

One of the blades is painted a different colour than the others. The end of this blade is labelled point $D$ . The height $h$ , in metres, of point $D$ above the ground can be modelled by the function $h (t) = p \cos (\frac{3 π}{10} t) + q$ , where $t$ is in seconds and $p, q \in ℝ$ . When $t = 0$ , point $D$ is at its maximum height.

Given that point $A$ is $12$ metres from the base of the windmill, find the height of point $C$ above the ground.

[2]

Find the angle of elevation of point $C$ from point $B$ .

[2]

Find the length of each blade of the windmill.

[2]

Find the value of $p$ and the value of $q$ .

[4]

If the observer stands directly under point $C$ for one minute, point $D$ will pass over his head $n$ times.

Find the value of $n$ .

[3]

Markscheme

$\tan 0.6 = \frac{h}{12}$ (M1)

$8.20964 \dots$

$8.21 (m)$ A1

[2 marks]

$\tan B = \frac{8.2096 \dots}{5}$ OR $\tan^{- 1} 1.6419 \dots$ (A1)

$1.02375 \dots$

$1.02$ (radians) (accept $58.7 °$ ) A1

[2 marks]

$x + 1.8 + 2.5 = 8.20964 \dots$ (or equivalent) (A1)

$3.90964 \dots$

$3.91$ ( $m$ ) A1

[2 marks]

METHOD 1

recognition that blade length = amplitude, $p = \frac{max - min}{2}$ (M1)

$p = 3.91$ A1

centre of windmill = vertical shift, $q = \frac{max + min}{2}$ (M1)

$q = 8.21$ A1

METHOD 2

attempting to form two equations in terms of $p$ and $q$ (M1)(M1)

$12.1192 \dots = p \cos (\frac{3 π}{10} \cdot 0) + q, 4.3000 \dots = p \cos (\frac{3 π}{10} \cdot \frac{10}{3}) + q$

$p = 3.91$ A1

$q = 8.21$ A1

[4 marks]

appropriate working towards finding the period (M1)

$period = \frac{2 π}{\frac{3 π}{10}} (= 6.6666 \dots)$

rotations per minute $= \frac{60}{their period}$ (M1)

$n = 9$ (must be an integer) (accept $n = 10$ , $n = 18$ , $n = 19$ ) A1

[3 marks]

Examiners report

[N/A]

Syllabus sections

Topic 3— Geometry and trigonometry » SL 3.3—Applications: angles of elevation and depression, bearings

Show 26 related questions

SPM.2.SL.TZ0.7b.i:
Show that ${\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}}$ is 101°.
19M.1.SL.TZ1.T_8a:
Draw and label the angle of depression on the diagram.
18M.1.SL.TZ1.T_8a:
On the diagram, draw and label with an x the angle of depression of B from P.
SPM.2.SL.TZ0.7e:
Jacob hikes at an average speed of 3.9 km/h.

Find, to the nearest minute, the time it takes for Jacob to reach point C.
19M.2.SL.TZ2.S_3a:
Find BD.
SPM.2.SL.TZ0.7a:
Find the distance from point A to point B.
SPM.2.SL.TZ0.7b.ii:
Find the distance from the camp to point C.
19M.2.SL.TZ2.S_3b:
The area of triangle ABD is 18.5 cm². Find the possible values of θ.
16N.1.SL.TZ0.T_11b:
Calculate the angle of depression from A to B.
21M.2.SL.TZ1.8e.ii:
Find the length of new fence required.
18N.2.SL.TZ0.S_7a:
Let SR = $x$ . Use the cosine rule to show that ${x^2} - \left( {76\,{\text{cos}}\,43^\circ } \right)x + 420 = 0$ .
21M.2.SL.TZ1.8e.i:
Find the size of $A \hat{B} C$ .
21M.2.SL.TZ2.7b:
Find the angle of elevation of point $C$ from point $B$ .
SPM.2.SL.TZ0.7c:
Find ${\text{B}}\mathop {\text{C}}\limits^ \wedge {\text{A}}$ .
SPM.2.SL.TZ0.7d:
Find the bearing that Jacob must take to point C.
22M.2.AHL.TZ2.11a:
Find the three-figure bearing on which airplane $B$ is travelling.
17N.1.SL.TZ0.T_10b:
Write down the angle of elevation of B from E.
17N.1.SL.TZ0.S_4a:
Show that ${\text{AC}} = 7{\text{ cm}}$ .
17N.2.AHL.TZ0.H_5:
Barry is at the top of a cliff, standing 80 m above sea level, and observes two yachts in the sea.
“Seaview” $(S)$ is at an angle of depression of 25°.
“Nauti Buoy” $(N)$ is at an angle of depression of 35°.
The following three dimensional diagram shows Barry and the two yachts at S and N.
X lies at the foot of the cliff and angle ${\text{SXN}} =$ 70°.

Find, to 3 significant figures, the distance between the two yachts.
21M.2.SL.TZ2.7c:
Find the length of each blade of the windmill.
17M.1.SL.TZ1.S_3:
The following diagram shows triangle PQR.

Find PR.
17N.1.SL.TZ0.S_4b:
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

Find the exact perimeter of this shape.
18N.2.SL.TZ0.S_7b:
Hence or otherwise, find the total distance along the road where the signal from the tower can reach cellular phones.
19M.1.SL.TZ2.T_9a:
Find the angle of elevation from B to C.
16N.1.SL.TZ0.T_11a:
Calculate CD, the height of the observation deck above the ground.
18N.2.SL.TZ0.T_5d:
A vertical pole, TB, is constructed at point B and has height 25 m.

Calculate the angle of elevation of T from, M, the midpoint of the side AC.

Hide related questions

Topic 3— Geometry and trigonometry

Question

Markscheme

Examiners report

Syllabus sections

View options