IB Questionbank

Updates to Questionbank

User interface language: English | Español

Date	November 2020	Marks available	1	Reference code	20N.2.SL.TZ0.S_7
Level	Standard Level	Paper	Paper 2	Time zone	Time zone 0
Command term	Show that	Question number	S_7	Adapted from	N/A

Question

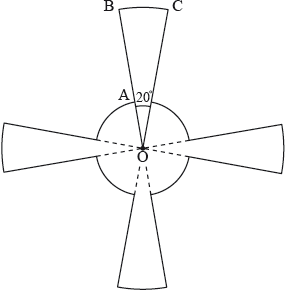
The following diagram shows a circle with centre $O$ $O$ and radius $1 cm$ $1 cm$ . Points $A$ $A$ and $B$ $B$ lie on the circumference of the circle and $A ˆ O B = 2 θ$ $A \hat{O} B = 2 θ$ , where $0 < θ < \frac{π}{2}$ $0 < θ < \frac{π}{2}$ .

The tangents to the circle at $A$ $A$ and $B$ $B$ intersect at point $C$ $C$ .

Show that $AC = tan θ$ $AC = \tan θ$ .

[1]

a.

Find the value of $θ$ $θ$ when the area of the shaded region is equal to the area of sector $OADB$ $OADB$ .

[6]

b.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

correct working for $AC$ $AC$ (seen anywhere) A1

eg $tan θ = \frac{AC}{OA}, tan θ = \frac{AC}{1}$ $\tan θ = \frac{AC}{OA}, \tan θ = \frac{AC}{1}$

$AC = tan θ$ $AC = \tan θ$ AG N0

[1 mark]

a.

METHOD 1 (working with half the areas)

area of triangle $OAC$ $OAC$ or triangle $OBC$ $OBC$ (A1)

eg $\frac{1}{2} \times 1 \times tan θ$ $\frac{1}{2} \times 1 \times \tan θ$

correct sector area (A1)

eg $\frac{1}{2} \times θ \times (1^{2}), \frac{1}{2} θ$ $\frac{1}{2} \times θ \times (1^{2}), \frac{1}{2} θ$

correct approach using their areas to find the shaded area (seen anywhere) (A1)

eg $A_{their triangle} - A_{their sector}, \frac{1}{2} θ - \frac{1}{2} tan θ$ $A_{their triangle} - A_{their sector}, \frac{1}{2} θ - \frac{1}{2} \tan θ$

correct equation A1

eg $\frac{1}{2} tan θ - \frac{1}{2} θ = \frac{1}{2} θ, tan θ = 2 θ$ $\frac{1}{2} \tan θ - \frac{1}{2} θ = \frac{1}{2} θ, \tan θ = 2 θ$

$1.16556$ $1.16556$

$1.17$ $1.17$ A2 N4

METHOD 2 (working with entire kite and entire sector)

area of kite $OACB$ $OACB$ (A1)

eg $2 \times \frac{1}{2} \times 1 \times tan θ, \frac{1}{2} \times \frac{1}{cos θ} \times 2 sin θ$ $2 \times \frac{1}{2} \times 1 \times \tan θ, \frac{1}{2} \times \frac{1}{\cos θ} \times 2 \sin θ$

correct sector area (A1)

eg $\frac{1}{2} \times 2 θ \times (1^{2}), θ$ $\frac{1}{2} \times 2 θ \times (1^{2}), θ$

correct approach using their areas to find the shaded area (seen anywhere) (A1)

eg $A_{kite OACB} - A_{sector OADB}, θ - tan θ$ $A_{kite OACB} - A_{sector OADB}, θ - \tan θ$

correct equation A1

eg $tan θ - θ = θ, tan θ = 2 θ$ $\tan θ - θ = θ, \tan θ = 2 θ$

$1.16556$ $1.16556$

$1.17$ $1.17$ A2 N4

[6 marks]

b.

Examiners report

[N/A]

a.

[N/A]

b.

Syllabus sections

Topic 3— Geometry and trigonometry » SL 3.4—Circle: radians, arcs, sectors

Show 57 related questions

22M.2.SL.TZ2.1b:
Find the area of the shaded sector.
18N.2.AHL.TZ0.H_7:
Boat A is situated 10km away from boat B, and each boat has a marine radio transmitter on board. The range of the transmitter on boat A is 7km, and the range of the transmitter on boat B is 5km. The region in which both transmitters can be detected is represented by the shaded region in the following diagram. Find the area of this region.
18M.2.SL.TZ1.S_3b:
The area of the shaded region is 12 cm². Find the value of θ.
19M.1.AHL.TZ1.H_3:
A sector of a circle with radius $r$ $r$ cm , where $r$ $r$ > 0, is shown on the following diagram.
The sector has an angle of 1 radian at the centre.

Let the area of the sector be $A$ $A$ cm² and the perimeter be $P$ $P$ cm. Given that $A = P$ , find the value of $r$ .
17M.2.SL.TZ1.S_5:
The following diagram shows the chord [AB] in a circle of radius 8 cm, where ${\text{AB}} = 12{\text{ cm}}$ .

Find the area of the shaded segment.
16N.2.SL.TZ0.S_3b:
Find the value of $r$ .
16N.2.AHL.TZ0.H_9c:
Hence find the value of $r$ given that the shaded area is equal to 4.
18M.2.AHL.TZ2.H_4a.ii:
Find ${\text{A}}\mathop {\text{M}}\limits^ \wedge {\text{P}}$ in radians.
18M.2.AHL.TZ2.H_4a.i:
Find AM.
21M.1.SL.TZ2.1a:
Find the value of $r$ .
16N.2.SL.TZ0.S_3a:
Write down the exact value of $\theta$ in radians.
19M.2.SL.TZ2.S_4c:
Given that the area of triangle OBC is $\frac{3}{5}$ of the area of sector OAB, find θ.
22M.2.SL.TZ1.3b:
Given that the area of the logo is $13.4 {cm}^{2}$ , find the value of $θ$ .
20N.2.AHL.TZ0.H_11e.i:
Show that, at these times, $\tan 6 t = 2$ .
21M.2.SL.TZ1.8e.ii:
Find the length of new fence required.
20N.2.AHL.TZ0.H_11c:
Find the maximum displacement of $P$ , in metres, from its initial position.
18M.2.AHL.TZ2.H_4b:
Find the area of the shaded region.
17M.2.AHL.TZ1.H_8b:
Calculate $\frac{{{\text{d}}\theta }}{{{\text{d}}t}}$ when $\theta = \frac{\pi }{3}$ .
21M.2.SL.TZ1.8a:
Write down an expression for $r$ in terms of $θ$ .
21M.2.SL.TZ1.8e.i:
Find the size of $A \hat{B} C$ .
16N.2.AHL.TZ0.H_9a:
Find an expression for the shaded area in terms of $\alpha$ , $\theta$ and $r$ .
20N.2.AHL.TZ0.H_11b:
Find an expression for $s$ in terms of $t$ .
18M.2.SL.TZ1.S_3a:
Find the area of the shaded region, in terms of θ.
20N.2.SL.TZ0.S_7b:
Find the value of $θ$ when the area of the shaded region is equal to the area of sector $OADB$ .
21M.3.AHL.TZ1.2c:
Show that $y = 2 x \sin \frac{π}{n}$ .
21M.3.AHL.TZ1.2d:
Use the results from parts (b) and (c) to show that $A = P = 4 n \tan \frac{π}{n}$ .
16N.2.AHL.TZ0.H_9b:
Show that $\alpha = 4\arcsin \frac{1}{4}$ .
19N.2.SL.TZ0.S_4a:
Find ${\text{B}}\widehat {\text{A}}{\text{C}}$ .
21M.2.SL.TZ1.8b:
Show that the area of the field that the horse can reach is $\frac{392}{θ^{2}} (θ + \sin θ)$ .
17M.2.SL.TZ2.S_1a:
Find the length of arc ABC.
19M.2.SL.TZ2.S_4a:
Show that ${\text{OC}} = r\,{\text{cos}}\,\theta$ .
18M.1.SL.TZ2.S_4:
The following diagram shows a circle with centre O and radius r cm.

The points A and B lie on the circumference of the circle, and ${\text{A}}\mathop {\text{O}}\limits^ \wedge {\text{B}}$ = θ. The area of the shaded sector AOB is 12 cm² and the length of arc AB is 6 cm.

Find the value of r.
EXN.2.SL.TZ0.2b:
Show that $L = \sqrt{18 - 18 \cos θ}$ .
21M.2.SL.TZ1.8d:
Hence, find the size of $D \hat{A} E$ .
19N.2.AHL.TZ0.H_4b:
the area.
22M.2.SL.TZ2.1a:
Find the length of the chord $[AB]$ .
21N.2.SL.TZ0.5b:
Hence determine the value of $θ$ .
22M.2.SL.TZ1.3a:
Find the area of one of the shaded segments in terms of $θ$ .
21N.2.SL.TZ0.5a:
Given that the areas of the two shaded regions are equal, show that $θ = 2 \sin θ$ .
17M.2.SL.TZ2.S_1b:
Find the perimeter of sector OABC.
17M.2.AHL.TZ1.H_8a:
Find an expression for the volume of water $V{\text{ }}({{\text{m}}^3})$ in the trough in terms of $\theta$ .
16N.2.SL.TZ0.S_3c:
Find AB.
17N.1.SL.TZ0.S_4a:
Show that ${\text{AC}} = 7{\text{ cm}}$ .
19M.2.SL.TZ2.S_4b:
Find the area of triangle OBC in terms of $r$ and θ.
SPM.2.SL.TZ0.2b:
Find the area of the shaded region.
20N.2.AHL.TZ0.H_11a:
Find the times when $P$ comes to instantaneous rest.
20N.2.AHL.TZ0.H_11e.ii:
Hence show that $\frac{v_{2}}{v_{1}} = \frac{v_{3}}{v_{2}} = - e^{- \frac{π}{2}}$ .
19N.2.AHL.TZ0.H_4a:
the perimeter.
20N.2.AHL.TZ0.H_11d:
Find the total distance travelled by $P$ in the first $1.5$ seconds of its motion.
SPM.2.SL.TZ0.2a:
Find the value of θ, giving your answer in radians.
17N.2.AHL.TZ0.H_3:
This diagram shows a metallic pendant made out of four equal sectors of a larger circle of radius ${\text{OB}} = 9{\text{ cm}}$ and four equal sectors of a smaller circle of radius ${\text{OA}} = 3{\text{ cm}}$ .
The angle ${\text{BOC}} =$ 20°.

Find the area of the pendant.
19N.2.SL.TZ0.S_4b:
Find the area of $R$ .
17M.2.SL.TZ2.S_1c:
Find the area of sector OABC.
17N.1.SL.TZ0.S_4b:
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

Find the exact perimeter of this shape.
EXN.2.SL.TZ0.2a:
Show that arc $APB$ has length $6 π - 3 θ$ .
21M.2.SL.TZ1.8c:
The area of field that the horse can reach is $460 m^{2}$ . Find the value of $θ$ .
21M.1.SL.TZ2.1b:
Hence, find the exact area of the non-shaded region.

Hide related questions

Topic 3— Geometry and trigonometry