IB Questionbank

User interface language: English | Español

Date	May 2017	Marks available	3	Reference code	17M.2.SL.TZ2.T_4
Level	Standard Level	Paper	Paper 2	Time zone	Time zone 2
Command term	Find	Question number	T_4	Adapted from	N/A

Question

The quadrilateral ABCD represents a park, where ${\text{AB}} = 120{\text{ m}}$ , ${\text{AD}} = 95{\text{ m}}$ and ${\text{DC}} = 100{\text{ m}}$ . Angle DAB is 70° and angle DCB is 110°. This information is shown in the following diagram.

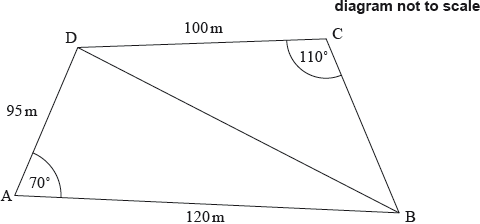
M17/5/MATSD/SP2/ENG/TZ2/04

A straight path through the park joins the points B and D.

A new path, CE, is to be built such that E is the point on BD closest to C.

The section of the park represented by triangle DCE will be used for a charity race. A track will be marked along the sides of this section.

Find the length of the path BD.

[3]

Show that angle DBC is 48.7°, correct to three significant figures.

[3]

Find the area of the park.

[4]

Find the length of the path CE.

[2]

Calculate the total length of the track.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$({\text{B}}{{\text{D}}^2} = ){\text{ }}{95^2} + {120^2} - 2 \times 95 \times 120 \times \cos 70^\circ$ (M1)(A1)

Note: Award (M1) for substituted cosine rule, (A1) for correct substitution.

$({\text{BD}} = ){\text{ }}125{\text{ (m) }}\left( {125.007 \ldots {\text{ (m)}}} \right)$ (A1)(G2)

[3 marks]

$\frac{{\sin {\text{DBC}}}}{{100}} = \frac{{\sin 110^\circ }}{{125.007 \ldots }}$ (M1)(A1)(ft)

Note: Award (M1) for substituted sine rule, (A1)(ft) for correct substitution.

Follow through from their answer to part (a).

$({\text{DBC}} = ){\text{ }}48.7384 \ldots ^\circ$ (A1)(ft)

$({\text{DBC}} = ){\text{ }}48.7^\circ$ (AG)

Notes: Award the final (A1)(ft) only if both their unrounded answer and 48.7° is seen. Follow through from their answer to part (a), only if their unrounded answer rounds to 48.7°.

[3 marks]

$\frac{1}{2} \times 125.007 \ldots \times 100 \times \sin 21.3^\circ + \frac{1}{2} \times 95 \times 120 \times \sin 70^\circ$ (A1)(M1)(M1)

Note: Award (A1) for 21.3° (21.2615…) seen, (M1) for substitution into (at least) one area of triangle formula in the form $\frac{1}{2}ab\sin c$ , (M1) for their correct substitutions and adding the two areas.

$7630{\text{ }}{{\text{m}}^2}{\text{ }}(7626.70 \ldots {{\text{m}}^2})$ (A1)(ft)(G3)

Notes: Follow through from their answers to part (a). Accept $7620{\text{ }}{{\text{m}}^2}{\text{ }}(7622.79 \ldots {{\text{m}}^2})$ from use of 48.7384…

[4 marks]

$({\text{CE}} = ){\text{ }}100 \times \sin 21.3^\circ$ (M1)

$({\text{CE}} = ){\text{ }}36.3{\text{ (m) }}\left( {36.3251 \ldots {\text{ (m)}}} \right)$ (A1)(ft)(G2)

Note: Follow through from their angle 21.3° in part (c). Award (M0)(A0) for halving 110° and/or assuming E is the midpoint of BD in any method seen.

${\text{area of BCD}} = \frac{1}{2}{\text{BD}} \times {\text{CE}}$ (M1)

$({\text{CE}} = ){\text{ }}36.3{\text{ (m) }}\left( {36.3251 \ldots {\text{ (m)}}} \right)$ (A1)(ft)(G2)

Note: Follow through from parts (a) and (c). Award (M0)(A0) for halving 110° and/or assuming E is the midpoint of BD in any method seen.

[2 marks]

$\sqrt {{{100}^2} - 36.3251{ \ldots ^2}} + 100 + 36.3251 \ldots$ (M1)(M1)

Note: Award (M1) for correct use of Pythagoras to find DE (or correct trigonometric equation, $100 \times \cos 21.3$ , to find DE), (M1) for the sum of 100, their DE and their CE.

$229{\text{ (m) }}\left( {229.494 \ldots {\text{ (m)}}} \right)$ (A1)(ft)(G2)

Note: Follow through from part (d). Use of 3 sf values gives an answer of $230{\text{ (m) }}\left( {229.5{\text{ (m)}}} \right)$ .

[3 marks]

Examiners report

[N/A]

Syllabus sections

Topic 3— Geometry and trigonometry » SL 3.2—2d and 3d trig, sine rule, cosine rule, area

Show 133 related questions

18M.1.SL.TZ2.T_8b:
Calculate the area of the park.
22M.2.SL.TZ2.1b:
Find the area of the shaded sector.
SPM.2.SL.TZ0.7b.i:
Show that ${\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}}$ is 101°.
19M.1.SL.TZ1.T_8a:
Draw and label the angle of depression on the diagram.
18M.1.SL.TZ1.T_8c:
Find the size of the angle of depression of B from P.
18M.1.SL.TZ1.T_8a:
On the diagram, draw and label with an x the angle of depression of B from P.
17N.2.SL.TZ0.S_1b:
Find the area of triangle ABC.
18M.2.SL.TZ1.T_1d:
Calculate the length of AE.
SPM.2.SL.TZ0.7e:
Jacob hikes at an average speed of 3.9 km/h.

Find, to the nearest minute, the time it takes for Jacob to reach point C.
19N.1.SL.TZ0.S_9a.i:
$\overrightarrow {{\text{OA}}} \bullet \overrightarrow {{\text{OC}}}$ .
18N.2.AHL.TZ0.H_11a:
Find an expression for ${\theta _p}$ in terms of $p$ .
18N.2.AHL.TZ0.H_11b:
Show that $p = \frac{{{q^2} + q - 1}}{{2q + 1}}$ .
19N.1.AHL.TZ0.H_9b:
Show that ${\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{D}} = 75^\circ$ .
17N.2.SL.TZ0.T_3c:
Find the area of ABCD.
19M.2.SL.TZ2.S_3a:
Find BD.
SPM.1.SL.TZ0.1a:
Given that ${\text{cos}}\,\hat A = \frac{5}{6}$ find the value of ${\text{sin}}\,\hat A$ .
SPM.2.SL.TZ0.7a:
Find the distance from point A to point B.
SPM.2.SL.TZ0.7b.ii:
Find the distance from the camp to point C.
17M.2.AHL.TZ2.H_4b:
The triangle ABC is shown in the following diagram. Given that $\cos B < \frac{1}{4}$ , find the range of possible values for AB.
18N.2.AHL.TZ0.H_11c:
By sketching the graph of $p$ as a function of $q$ , determine the range of values of $p$ for which there are possible values of $q$ .
19M.2.SL.TZ2.S_3b:
The area of triangle ABD is 18.5 cm². Find the possible values of θ.
16N.1.SL.TZ0.T_11b:
Calculate the angle of depression from A to B.
17M.1.SL.TZ2.T_3b:
Find the total length of wire needed to construct this wireframe. Give your answer in centimetres correct to the nearest millimetre.
19N.2.SL.TZ0.S_6:
The diagram below shows a triangular-based pyramid with base ${\text{ADC}}$ .
Edge ${\text{BD}}$ is perpendicular to the edges ${\text{AD}}$ and ${\text{CD}}$ .

${\text{AC}} = 28.4\,{\text{cm}}$ , ${\text{AB}} = x\,{\text{cm}}$ , ${\text{BC}} = x + 2\,{\text{cm}}$ , ${\text{A}}\widehat {\text{B}}{\text{C}} = 0.667$ , ${\text{B}}\widehat {\text{A}}{\text{D}} = 0.611$

Calculate ${\text{AD}}$
19N.1.SL.TZ0.S_9a.ii:
$\overrightarrow {{\text{OB}}} \bullet \overrightarrow {{\text{OC}}}$ .
22M.2.SL.TZ1.7b:
Given that $A \hat{V} B = 40 °$ , find $AB$ .
22M.2.SL.TZ2.7b:
Find the area of this piece of land.
22M.2.SL.TZ2.7c:
Find $CÂB$ .
22M.2.SL.TZ2.7d:
Find the distance from point $B$ to point $D$ .
20N.1.SL.TZ0.S_2a:
Given that $A \hat{B} C$ is acute, find $\sin θ$ .
20N.1.SL.TZ0.S_2b:
Find $\cos (2 \times C \hat{A} B)$ .
20N.2.SL.TZ0.T_3b:
Show that angle $EDC = 48.0 °$ , correct to three significant figures.
21M.2.SL.TZ1.8e.ii:
Find the length of new fence required.
18M.1.SL.TZ2.T_8a:
Calculate the length of side AC in km.
SPM.1.SL.TZ0.1b:
Find the area of triangle ABC.
18N.2.SL.TZ0.S_7a:
Let SR = $x$ . Use the cosine rule to show that ${x^2} - \left( {76\,{\text{cos}}\,43^\circ } \right)x + 420 = 0$ .
16N.2.SL.TZ0.T_5d:
the area of quadrilateral ABCD;
21M.2.SL.TZ1.8a:
Write down an expression for $r$ in terms of $θ$ .
21M.2.SL.TZ1.8e.i:
Find the size of $A \hat{B} C$ .
21M.3.AHL.TZ1.2c:
Show that $y = 2 x \sin \frac{π}{n}$ .
21M.3.AHL.TZ1.2d:
Use the results from parts (b) and (c) to show that $A = P = 4 n \tan \frac{π}{n}$ .
17M.2.AHL.TZ2.H_4a:
Find the set of values of $k$ that satisfy the inequality ${k^2} - k - 12 < 0$ .
18M.1.SL.TZ1.T_8b:
Find the size of angle APB.
19N.1.SL.TZ0.S_9b:
Given that ${\text{A}}\widehat {\text{O}}{\text{C}} = {\text{B}}\widehat {\text{O}}{\text{C}}$ , show that $k = 7$ .
21M.2.SL.TZ1.8b:
Show that the area of the field that the horse can reach is $\frac{392}{θ^{2}} (θ + \sin θ)$ .
19M.1.AHL.TZ1.H_4a:
Show that ${\text{sin}}\,\theta = \frac{{\sqrt {15} }}{4}$ .
19N.1.AHL.TZ0.H_9c.i:
By considering triangle ${\text{ABD}}$ , show that ${\text{B}}{{\text{D}}^2} = 5{r^2} - 2{r^2}q\sqrt 6$ .
19N.1.AHL.TZ0.H_9d:
Use your answers to part (c) to show that ${\text{cos}}\,75^\circ = \frac{1}{{\sqrt 6 + \sqrt 2 }}$ .
EXN.2.SL.TZ0.2b:
Show that $L = \sqrt{18 - 18 \cos θ}$ .
17N.2.SL.TZ0.S_1a:
Find BC.
SPM.2.SL.TZ0.7c:
Find ${\text{B}}\mathop {\text{C}}\limits^ \wedge {\text{A}}$ .
21M.2.SL.TZ1.8d:
Hence, find the size of $D \hat{A} E$ .
SPM.2.SL.TZ0.7d:
Find the bearing that Jacob must take to point C.
EXN.1.AHL.TZ0.7:
Consider quadrilateral $PQRS$ where $[PQ]$ is parallel to $[SR]$ .

In $PQRS$ , $PQ = x$ , $SR = y$ , $R \hat{S} P = α$ and $Q \hat{R} S = β$ .

Find an expression for $PS$ in terms of $x, y, \sin β$ and $\sin (α + β)$ .
22M.2.SL.TZ2.1a:
Find the length of the chord $[AB]$ .
21N.2.SL.TZ0.5b:
Hence determine the value of $θ$ .
22M.2.SL.TZ2.7a:
Find the distance from point $A$ to point $C$ .
18M.2.SL.TZ1.T_1c:
Calculate the length of MN.
19M.2.SL.TZ1.T_2c:
Find the maximum number of complete panels that can be fitted to the whole roof.
17N.1.SL.TZ0.T_10b:
Write down the angle of elevation of B from E.
18M.2.SL.TZ2.T_5c:
Giovanni adds a point D to his diagram, such that BD = 45 m, and another triangle is formed.

Find the angle of elevation of A from D.
17N.1.SL.TZ0.T_10c:
Find the vertical height of B above the ground.
19M.1.SL.TZ2.T_9b:
A second truck arrives whose ladder, when fully extended, is 30 metres long. The base of this ladder is also 4 metres above the ground. For safety reasons, the maximum angle of elevation that the ladder can make is 70º.

Find the maximum height on the wall that can be reached by the ladder on the second truck.
16N.2.SL.TZ0.T_5f:
the length of the fence, BP.
17M.2.SL.TZ1.T_2a.i:
Write down an equation for the area of ABCDE using the above information.
17N.1.SL.TZ0.T_10a:
Find the length of EB.
19M.1.SL.TZ1.T_10b:
Find the area, in km², of triangle ABC.
21N.2.SL.TZ0.5a:
Given that the areas of the two shaded regions are equal, show that $θ = 2 \sin θ$ .
19M.1.SL.TZ1.S_3a:
Given that ${\text{sin}}\,\theta = \frac{3}{5}$ , find the value of ${\text{cos}}\,\theta$ .
19M.1.SL.TZ1.S_3b:
Find the value of ${\text{cos}}\,2\theta$ .
19M.2.AHL.TZ2.H_1:
In triangle ABC, AB = 5, BC = 14 and AC = 11.

Find all the interior angles of the triangle. Give your answers in degrees to one decimal place.
18N.2.SL.TZ0.T_5b:
Calculate the area of triangle ABC.
19N.1.AHL.TZ0.H_9c.ii:
By considering triangle ${\text{CBD}}$ , find another expression for ${\text{B}}{{\text{D}}^2}$ in terms of $r$ and $q$ .
17N.1.SL.TZ0.S_4a:
Show that ${\text{AC}} = 7{\text{ cm}}$ .
17M.1.SL.TZ2.T_3a:
Find the length of one of the straight pieces in the wireframe.
19M.1.SL.TZ1.S_3c:
Hence or otherwise, find ${\text{BC}}$ .
19N.1.AHL.TZ0.H_9a:
Given that ${\text{cos}}\,75^\circ = q$ , show that ${\text{cos}}\,105^\circ = - q$ .
19N.1.SL.TZ0.S_9c:
Calculate the area of triangle ${\text{AOC}}$ .
17M.1.SL.TZ1.S_3:
The following diagram shows triangle PQR.

Find PR.
19M.1.AHL.TZ1.H_4b:
Find the two possible values for the length of the third side.
17N.1.SL.TZ0.S_4b:
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

Find the exact perimeter of this shape.
18M.2.SL.TZ2.S_2a:
Find DB.
18M.2.SL.TZ2.S_2b:
Find DC.
EXN.2.SL.TZ0.2a:
Show that arc $APB$ has length $6 π - 3 θ$ .
18N.2.SL.TZ0.S_7b:
Hence or otherwise, find the total distance along the road where the signal from the tower can reach cellular phones.
21M.1.SL.TZ2.6:
The following diagram shows triangle $ABC$ , with $AB = 10$ , $BC = x$ and $AC = 2 x$ .

Given that $\cos \hat{C} = \frac{3}{4}$ , find the area of the triangle.

Give your answer in the form $\frac{p \sqrt{q}}{2}$ where $p, q \in ℤ^{+}$ .
21M.2.SL.TZ1.8c:
The area of field that the horse can reach is $460 m^{2}$ . Find the value of $θ$ .
21N.2.SL.TZ0.3:
Consider a triangle $ABC$ , where $AC = 12, CB = 7$ and $B \hat{A} C = 25 °$ .

Find the smallest possible perimeter of triangle $ABC$ .
17M.2.SL.TZ2.T_4e:
Calculate the total length of the track.
17M.1.SL.TZ1.T_13a:
Find the length of BC.
18N.2.SL.TZ0.T_5c:
Find the length of AC.
16N.2.SL.TZ0.T_5b:
the size of angle DAB;
19M.1.SL.TZ2.T_9a:
Find the angle of elevation from B to C.
17M.2.SL.TZ2.T_4b:
Show that angle DBC is 48.7°, correct to three significant figures.
17M.1.SL.TZ1.T_13b:
Find the area of the postage stamp.
20N.2.SL.TZ0.T_3d:
Pedro draws a circle, with centre at point $E$ , passing through point $C$ . Part of the circle is shown in the diagram.

Show that point $A$ lies outside this circle. Justify your reasoning.
17M.2.SL.TZ1.T_2c:
Show that angle ${\rm{B\hat AE}} = 67.4^\circ$ , correct to one decimal place.
17M.2.SL.TZ2.T_4d:
Find the length of the path CE.
16N.2.SL.TZ0.T_5a:
the length of BD;
19M.2.SL.TZ2.T_2d:
The length of path AD is 287 m.

Find the area of the region ABCD.
16N.1.SL.TZ0.T_11a:
Calculate CD, the height of the observation deck above the ground.
19M.1.SL.TZ1.T_10a:
Find the size, in degrees, of angle BÂC.
18M.2.SL.TZ1.T_1e:
Show that Farmer Brown is incorrect.
17M.2.SL.TZ1.T_2d:
Find the length of the perimeter of ABCDE.
18N.2.SL.TZ0.T_5a:
Show that the size of angle BÂC is 20.2°, correct to 3 significant figures.
18M.2.SL.TZ2.T_5a.i:
Use Giovanni’s diagram to show that angle ABC, the angle at which the Tower is leaning relative to the
horizontal, is 85° to the nearest degree.
18M.2.SL.TZ2.T_5a.ii:
Use Giovanni's diagram to calculate the length of AX.
18M.2.SL.TZ2.T_5a.iii:
Use Giovanni's diagram to find the length of BX, the horizontal displacement of the Tower.
18M.2.SL.TZ2.T_5b:
Find the percentage error on Giovanni’s diagram.
17N.2.SL.TZ0.T_3a:
Show that ${\text{BD}} = 93{\text{ m}}$ correct to the nearest metre.
17N.2.SL.TZ0.T_3b:
Calculate angle ${\rm{B\hat CD}}$ .
17N.2.SL.TZ0.T_3d.i:
Calculate Abdallah’s estimate for the area.
17N.2.SL.TZ0.T_3d.ii:
Find the percentage error in Abdallah’s estimate.
19M.2.SL.TZ1.T_2a:
Find the length ${\text{AB}}$ , giving your answer to four significant figures.
19M.2.SL.TZ1.T_2b:
Find the total area of the two rectangles that make up the roof.
19M.2.SL.TZ1.T_2d:
Find the percentage error in her estimate.
19M.2.SL.TZ1.T_2e:
Olivia investigates arranging the panels, such that the longer edge of each panel is parallel to ${\text{AB}}$ or ${\text{AC}}$ .

State whether this new arrangement will allow Olivia to fit more solar panels to the roof. Justify your answer.
19M.2.SL.TZ2.T_2a:
Find the distance from A to C.
19M.2.SL.TZ2.T_2b.i:
Find the size of angle ${\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{C}}$ .
19M.2.SL.TZ2.T_2b.ii:
Find the size of angle ${\text{C}}\mathop {\text{A}}\limits^ \wedge {\text{D}}$ .
19M.2.SL.TZ2.T_2c:
Find the size of angle ${\text{A}}\mathop {\text{C}}\limits^ \wedge {\text{D}}$ .
18M.2.SL.TZ1.T_1a:
Calculate the area of triangle EAD.
18M.2.SL.TZ1.T_1b:
Calculate the total volume of the barn.
18M.2.SL.TZ1.T_1f:
Calculate the total length of metal required for one support.
17M.2.SL.TZ1.T_2a.ii:
Show that the equation in part (a)(i) simplifies to $3{x^2} + 19x - 414 = 0$ .
17M.2.SL.TZ1.T_2b:
Find the length of CD.
17M.2.SL.TZ1.T_2e:
Calculate the length of CF.
18N.2.SL.TZ0.T_5d:
A vertical pole, TB, is constructed at point B and has height 25 m.

Calculate the angle of elevation of T from, M, the midpoint of the side AC.
17M.2.SL.TZ2.T_4c:
Find the area of the park.
16N.2.SL.TZ0.T_5c:
the area of triangle ABD;
16N.2.SL.TZ0.T_5e:
the length of AP;
20N.2.SL.TZ0.T_3a:
Calculate the length of $BD$ .
20N.2.SL.TZ0.T_3c:
Calculate the area of triangle $BDC$ .

Hide related questions

Topic 3— Geometry and trigonometry

Question

Markscheme

Examiners report

Syllabus sections

View options