IB Questionbank

User interface language: English | Español

Date	May 2017	Marks available	3	Reference code	17M.2.AHL.TZ1.H_8
Level	Additional Higher Level	Paper	Paper 2	Time zone	Time zone 1
Command term	Find	Question number	H_8	Adapted from	N/A

Question

A water trough which is 10 metres long has a uniform cross-section in the shape of a semicircle with radius 0.5 metres. It is partly filled with water as shown in the following diagram of the cross-section. The centre of the circle is O and the angle KOL is $\theta$ radians.

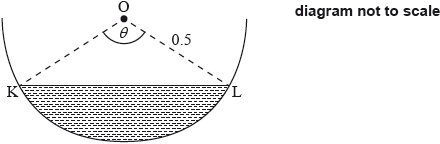
M17/5/MATHL/HP2/ENG/TZ1/08

The volume of water is increasing at a constant rate of $0.0008{\text{ }}{{\text{m}}^3}{{\text{s}}^{ - 1}}$ .

Find an expression for the volume of water $V{\text{ }}({{\text{m}}^3})$ in the trough in terms of $\theta$ .

[3]

Calculate $\frac{{{\text{d}}\theta }}{{{\text{d}}t}}$ when $\theta = \frac{\pi }{3}$ .

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

area of segment $= \frac{1}{2} \times {0.5^2} \times (\theta - \sin \theta )$ M1A1

$V = {\text{area of segment}} \times 10$

$V = \frac{5}{4}(\theta - \sin \theta )$ A1

[3 marks]

METHOD 1

$\frac{{{\text{d}}V}}{{{\text{d}}t}} = \frac{5}{4}(1 - \cos \theta )\frac{{{\text{d}}\theta }}{{{\text{d}}t}}$ M1A1

$0.0008 = \frac{5}{4}\left( {1 - \cos \frac{\pi }{3}} \right)\frac{{{\text{d}}\theta }}{{{\text{d}}t}}$ (M1)

$\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = 0.00128{\text{ }}({\text{rad}}\,{s^{ - 1}})$ A1

METHOD 2

$\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \frac{{{\text{d}}\theta }}{{{\text{d}}V}} \times \frac{{{\text{d}}V}}{{{\text{d}}t}}$ (M1)

$\frac{{{\text{d}}V}}{{{\text{d}}\theta }} = \frac{5}{4}(1 - \cos \theta )$ A1

$\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \frac{{4 \times 0.0008}}{{5\left( {1 - \cos \frac{\pi }{3}} \right)}}$ (M1)

$\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = 0.00128\left( {\frac{4}{{3125}}} \right)({\text{rad }}{s^{ - 1}})$ A1

[4 marks]

Examiners report

[N/A]

Syllabus sections

Topic 5 —Calculus » SL 5.3—Differentiating polynomials, n E Z

Show 91 related questions

18N.2.SL.TZ0.T_6a:
Calculate the area of cloth, in cm², needed to make Haruka’s bag.
19M.2.SL.TZ2.T_5b:
Write down the $y$ -intercept of the graph of $y = f\left( x \right)$ .
SPM.1.SL.TZ0.8b:
Find the value of $a$ and the value of $b$ .
18M.2.SL.TZ1.S_1c:
Solve f '(x) = f "(x).
16N.1.SL.TZ0.S_10c:
(i) Find $h'(x)$ .

(ii) Hence, show that $h'(\pi ) = \frac{{ - 21!}}{2}{\pi ^2}$ .
16N.1.SL.TZ0.S_10b:
(i) Find the first three derivatives of $g(x)$ .

(ii) Given that ${g^{(19)}}(x) = \frac{{k!}}{{(k - p)!}}({x^{k - 19}})$ , find $p$ .
17M.2.SL.TZ2.T_6f:
Write down the number of possible solutions to the equation $f(x) = 5$ .
18M.1.AHL.TZ1.H_7a:
Find $\frac{{{\text{d}}y}}{{{\text{d}}x}}$ .
SPM.1.SL.TZ0.8c.i:
Sketch the graph of $y = f'\left( x \right)$ .
17M.2.AHL.TZ1.H_12c:
Explain why $f$ is an even function.
17M.2.AHL.TZ1.H_12b:
Sketch the graph of $y = f(x)$ showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.
16N.1.SL.TZ0.S_10a:
(i) Find the first four derivatives of $f(x)$ .

(ii) Find ${f^{(19)}}(x)$ .
SPM.1.SL.TZ0.8a:
Find $f'\left( x \right)$ .
19N.2.SL.TZ0.S_3b:
Let ${\text{C}}$ be a point on the graph of $h$ . The tangent to the graph of $h$ at ${\text{C}}$ is parallel to the graph of $f$ .

Find the $x$ -coordinate of ${\text{C}}$ .
19M.2.SL.TZ2.T_5c:
Sketch the graph of $y = f\left( x \right)$ for −3 ≤ $x$ ≤ 3 and −4 ≤ $y$ ≤ 12.
19N.2.SL.TZ0.S_3a:
Find $h\left( x \right)$ .
18N.1.SL.TZ0.S_10b.i:
Find $f'\left( x \right)$ .
16N.1.SL.TZ0.T_14b:
Find the coordinates of P.
18M.1.SL.TZ2.S_9b:
Show that $C = 20\pi {r^2} + \frac{{320\pi }}{r}$ .
19M.1.SL.TZ2.S_10c:
Write down an expression for the area of $R$ .
18N.1.SL.TZ0.S_10c:
The graph of $f$ has a local minimum at the point Q. The line L passes through Q.

Find the value of $a$ .
17M.2.AHL.TZ1.H_2a:
Find $\frac{{{\text{d}}y}}{{{\text{d}}x}}$ in terms of $x$ and $y$ .
22M.1.SL.TZ2.7d:
Find the values of $d$ for which $g$ is an increasing function.
SPM.1.SL.TZ0.8c.ii:
Hence explain why the graph of $f$ has a local maximum point at $x = a$ .
19M.1.AHL.TZ1.H_7:
Find the coordinates of the points on the curve ${y^3} + 3x{y^2} - {x^3} = 27$ at which $\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0$ .
20N.1.SL.TZ0.T_13b:
Write down the gradient of this tangent.
SPM.1.SL.TZ0.8d.i:
Find $f''\left( b \right)$ .
17N.1.SL.TZ0.S_8d:
Find the area of the region enclosed by the graph of $f$ and the line $L$ .
17M.2.AHL.TZ1.H_8b:
Calculate $\frac{{{\text{d}}\theta }}{{{\text{d}}t}}$ when $\theta = \frac{\pi }{3}$ .
19M.1.SL.TZ2.S_10d:
Hence find the exact area of $R$ .
17M.2.AHL.TZ1.H_12d:
Explain why the inverse function ${f^{ - 1}}$ does not exist.
17M.2.AHL.TZ1.H_12g.i:
Hence, show that there are no solutions to $g'(x) = 0$ ;
17N.1.AHL.TZ0.H_7:
The folium of Descartes is a curve defined by the equation ${x^3} + {y^3} - 3xy = 0$ , shown in the following diagram.

Determine the exact coordinates of the point P on the curve where the tangent line is parallel to the $y$ -axis.
17N.2.SL.TZ0.T_5b.ii:
Find $f’(x)$ .
17M.2.AHL.TZ1.H_12a:
Find the largest possible domain $D$ for $f$ to be a function.
20N.1.SL.TZ0.S_10b:
Find the area of triangle $AOB$ in terms of $k$ .
21M.3.AHL.TZ1.1b:
Write down an expression for $f' (x)$ .
18M.1.SL.TZ1.S_7:
Consider f(x), g(x) and h(x), for x∈ $\mathbb{R}$ where h(x) = $\left( {f \circ g} \right)$ (x).

Given that g(3) = 7 , g′ (3) = 4 and f ′ (7) = −5 , find the gradient of the normal to the curve of h at x = 3.
17M.2.SL.TZ1.S_6:
Let $f(x) = {({x^2} + 3)^7}$ . Find the term in ${x^5}$ in the expansion of the derivative, $f’(x)$ .
17M.2.AHL.TZ1.H_12f:
Find $g'(x)$ .
18M.1.SL.TZ2.S_9a:
Express h in terms of r.
20N.1.SL.TZ0.S_10c:
The graph of $f$ is translated by $(\begin{matrix} 4 \\ 3 \end{matrix})$ to give the graph of $g$ .
In the following diagram:
- point $Q$ lies on the graph of $g$
- points $C$ , $D$ and $E$ lie on the vertical asymptote of $g$
- points $D$ and $F$ lie on the horizontal asymptote of $g$
- point $G$ lies on the $x$ -axis such that $FG$ is parallel to $DC$ .
Line $L_{2}$ is the tangent to the graph of $g$ at $Q$ , and passes through $E$ and $F$ .

Given that triangle $EDF$ and rectangle $CDFG$ have equal areas, find the gradient of $L_{2}$ in terms of $p$ .
19M.1.SL.TZ2.T_15c:
Hence, find the number of vases that will maximize the profit.
17M.2.AHL.TZ1.H_12e:
Find the inverse function ${g^{ - 1}}$ and state its domain.
20N.1.SL.TZ0.S_10a.ii:
Show that the equation of $L_{1}$ is $k x + p^{2} y - 2 p k = 0$ .
SPM.1.SL.TZ0.8e:
The normal to the graph of $f$ at $x = a$ and the tangent to the graph of $f$ at $x = b$ intersect at the point ( $p$ , $q$ ) .

Find the value of $p$ and the value of $q$ .
20N.1.SL.TZ0.S_10a.i:
Find $f' (p)$ in terms of $k$ and $p$ .
19M.1.SL.TZ1.T_15a:
Write down an equation for the area, $A$ , of the curved surface in terms of $r$ .
19M.1.SL.TZ2.T_15a:
Find the value of $P$ if no vases are sold.
17M.2.SL.TZ2.T_6d.i:
Write down the $x$ -coordinates of these two points;
17N.2.SL.TZ0.T_5b.i:
Expand the expression for $f(x)$ .
17M.1.SL.TZ1.S_9c:
The line $y = kx - 5$ is a tangent to the curve of $f$ . Find the values of $k$ .
16N.2.SL.TZ0.T_6b:
Express this volume in ${\text{c}}{{\text{m}}^3}$ .
16N.2.SL.TZ0.T_6c:
Write down, in terms of $r$ and $h$ , an equation for the volume of this water container.
16N.2.SL.TZ0.T_6e:
Find $\frac{{{\text{d}}A}}{{{\text{d}}r}}$ .
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of $r$ which minimizes $A$ .
18N.1.SL.TZ0.S_10b.ii:
Hence, find the equation of L in terms of $a$ .
18M.1.SL.TZ2.S_9c:
Given that there is a minimum value for C, find this minimum value in terms of $\pi$ .
16N.2.AHL.TZ0.H_6:
An earth satellite moves in a path that can be described by the curve $72.5{x^2} + 71.5{y^2} = 1$ where $x = x(t)$ and $y = y(t)$ are in thousands of kilometres and $t$ is time in seconds.

Given that $\frac{{{\text{d}}x}}{{{\text{d}}t}} = 7.75 \times {10^{ - 5}}$ when $x = 3.2 \times {10^{ - 3}}$ , find the possible values of $\frac{{{\text{d}}y}}{{{\text{d}}t}}$ .

Give your answers in standard form.
SPM.1.SL.TZ0.8d.ii:
Hence, use your answer to part (d)(i) to show that the graph of $f$ has a local minimum point at $x = b$ .
17M.2.AHL.TZ1.H_2b:
Determine the equation of the tangent to $C$ at the point $\left( {\frac{2}{{\text{e}}},{\text{ e}}} \right)$
19M.1.SL.TZ2.S_10b:
Hence find $\int {\left( {3{x^2} + 1} \right)\sqrt {{x^3} + x} } \,{\text{d}}x$ .
18M.1.AHL.TZ1.H_7b:
Find $\int_0^1 {{\text{arccos}}\left( {\frac{x}{2}} \right){\text{d}}x}$ .
17M.2.AHL.TZ1.H_12g.ii:
Hence, show that there are no solutions to $({g^{ - 1}})'(x) = 0$ .
16N.1.SL.TZ0.T_14a:
Find $\frac{{{\text{d}}y}}{{{\text{d}}x}}$ .
18M.1.AHL.TZ2.H_6b:
Hence, or otherwise, find $\int\limits_0^\pi {{{\text{e}}^{ - x}}\,{\text{sin}}\,x\,{\text{d}}x}$ .
18N.2.SL.TZ0.T_6g:
Use your answer to part (f) to show that the width of Nanako’s bag is 12 cm.
19M.1.SL.TZ1.T_15c:
Find the value of $r$ when the area of the curved surface is maximized.
18N.2.SL.TZ0.T_6d:
Write down and simplify an expression in x and y for the area of cloth, A, used to make Nanako’s bag.
19M.1.SL.TZ2.T_15b:
Differentiate $P\left( x \right)$ .
20N.1.SL.TZ0.T_13c:
Find the value of $k$ .
17M.2.SL.TZ2.T_6a:
Write down the $y$ -intercept of the graph.
17M.2.SL.TZ2.T_6c.i:
Show that $a = 8$ .
17M.2.SL.TZ2.T_6b:
Find $f'(x)$ .
20N.1.SL.TZ0.T_13a:
Write down $f' (x)$ .
19M.2.SL.TZ2.T_5h:
Determine the range of $f\left( x \right)$ for $p$ ≤ $x$ ≤ $q$ .
17N.2.SL.TZ0.T_5e:
Write down the coordinates of the point of intersection.
17M.2.SL.TZ2.T_6g:
The equation $f(x) = m$ , where $m \in \mathbb{R}$ , has four solutions. Find the possible values of $m$ .
16N.2.SL.TZ0.T_6d:
Show that $A = \pi {r^2} + \frac{{1\,000\,000}}{r}$ .
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
19M.1.SL.TZ1.T_15b:
Find $\frac{{{\text{d}}A}}{{{\text{d}}r}}$ .
18N.2.SL.TZ0.T_6e:
Use your answers to parts (c) and (d) to show that

$A = 3{x^2} + \frac{{10368}}{x}$ .
16N.2.SL.TZ0.T_6a:
Write down a formula for $A$ , the surface area to be coated.
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
17N.2.SL.TZ0.T_5d:
Draw the graph of $f$ for $- 3 \leqslant x \leqslant 3$ and $- 40 \leqslant y \leqslant 20$ . Use a scale of 2 cm to represent 1 unit on the $x$ -axis and 1 cm to represent 5 units on the $y$ -axis.
17M.2.SL.TZ2.T_6c.ii:
Find $f(2)$ .
17M.2.SL.TZ2.T_6d.ii:
Write down the intervals where the gradient of the graph of $y = f(x)$ is positive.
17M.2.SL.TZ2.T_6e:
Write down the range of $f(x)$ .
18N.2.SL.TZ0.T_6b:
Calculate the volume, in cm³, of the bag.
18N.2.SL.TZ0.T_6c:
Use this value to write down, and simplify, the equation in x and y for the volume of Nanako’s bag.
18N.2.SL.TZ0.T_6f:
Find $\frac{{{\text{d}}A}}{{{\text{d}}x}}$ .

Hide related questions

Topic 3— Geometry and trigonometry » SL 3.4—Circle: radians, arcs, sectors

Topic 5 —Calculus » SL 5.6—Differentiating polynomials n E Q. Chain, product and quotient rules

Topic 5 —Calculus » AHL 5.14—Implicit functions, related rates, optimisation

Topic 3— Geometry and trigonometry

Topic 5 —Calculus

Question

Markscheme

Examiners report

Syllabus sections

View options