IB Questionbank

User interface language: English | Español

Date	May 2017	Marks available	2	Reference code	17M.1.SL.TZ1.T_9
Level	Standard Level	Paper	Paper 1 (with calculator from previous syllabus)	Time zone	Time zone 1
Command term	Find	Question number	T_9	Adapted from	N/A

Question

A type of candy is packaged in a right circular cone that has volume ${\text{100 c}}{{\text{m}}^{\text{3}}}$ and vertical height 8 cm.

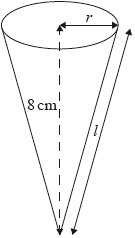
M17/5/MATSD/SP1/ENG/TZ1/09

Find the radius, $r$ , of the circular base of the cone.

[2]

Find the slant height, $l$ , of the cone.

[2]

Find the curved surface area of the cone.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$100 = \frac{1}{3}\pi {r^2}(8)$ (M1)

Note: Award (M1) for correct substitution into volume of cone formula.

$r = 3.45{\text{ (cm) }}\left( {3.45494 \ldots {\text{ (cm)}}} \right)$ (A1) (C2)

[2 marks]

${l^2} = {8^2} + {(3.45494 \ldots )^2}$ (M1)

Note: Award (M1) for correct substitution into Pythagoras’ theorem.

$l = 8.71{\text{ (cm) }}\left( {8.71416 \ldots {\text{ (cm)}}} \right)$ (A1)(ft) (C2)

Note: Follow through from part (a).

[2 marks]

$\pi \times 3.45494 \ldots \times 8.71416 \ldots$ (M1)

Note: Award (M1) for their correct substitutions into curved surface area of a cone formula.

$= 94.6{\text{ c}}{{\text{m}}^2}{\text{ }}(94.5836 \ldots {\text{ c}}{{\text{m}}^2})$ (A1)(ft) (C2)

Note: Follow through from parts (a) and (b). Accept $94.4{\text{ c}}{{\text{m}}^2}$ from use of 3 sf values.

[2 marks]

Examiners report

[N/A]

Syllabus sections

Topic 3— Geometry and trigonometry » SL 3.1—3d space, volume, angles, distance, midpoints

Show 73 related questions

18N.1.SL.TZ0.T_1b:
Write down your answer to part (a) correct to the nearest integer.
17M.2.SL.TZ1.T_4f:
In the context of this model, state what the value of 19 represents.
22M.1.AHL.TZ1.11b.i:
Verify that the point $P (1, - 2, 0)$ lies on both $\prod_{1}$ and $\prod_{2}$ .
18N.1.SL.TZ0.T_9a.i:
Write down the value of x.
22M.2.SL.TZ1.7c:
Find the height of the pyramid, $VX$ .
22M.2.SL.TZ1.7d:
A second ornament is in the shape of a cuboid with a rectangular base of length $2 x cm$ , width $x cm$ and height $y cm$ . The cuboid has the same volume as the pyramid.

The cuboid has a minimum surface area of $S {cm}^{2}$ . Find the value of $S$ .
17M.2.SL.TZ1.T_4c:
Find the value of $a$ .
18M.2.SL.TZ1.T_1d:
Calculate the length of AE.
SPM.2.SL.TZ0.1b:
The sphere is to be melted down and remoulded into the shape of a cone with a height of 14.8 cm.

Find the radius of the base of the cone, correct to 2 significant figures.
16N.1.SL.TZ0.T_7b:
Calculate the radius of the balloon following this increase.
22M.1.AHL.TZ1.11b.ii:
Find a vector equation of $L$ , the line of intersection of $\prod_{1}$ and $\prod_{2}$ .
22M.1.AHL.TZ1.11c:
Find the distance between $L$ and $\prod_{3}$ .
17N.2.SL.TZ0.T_6c:
Find the cost of $100{\text{ c}}{{\text{m}}^3}$ of chocolate mousse.
21M.1.SL.TZ1.2a:
Write down the radius of the planet.
21M.1.SL.TZ1.2b:
The volume of the planet can be expressed in the form $π (a \times 10^{k}) {km}^{3}$ where $1 \leq a < 10$ and $k \in ℤ$ .

Find the value of $a$ and the value of $k$ .
21M.1.SL.TZ2.8d:
Hence, find the volume of the cone.
22M.1.AHL.TZ1.11a:
Show that the three planes do not intersect.
22M.2.SL.TZ1.7a:
Find $AV$ .
18M.2.SL.TZ1.T_1c:
Calculate the length of MN.
19M.2.SL.TZ1.T_2c:
Find the maximum number of complete panels that can be fitted to the whole roof.
17N.2.SL.TZ0.T_6f:
Find the value of $x$ .
19M.1.SL.TZ1.T_15a:
Write down an equation for the area, $A$ , of the curved surface in terms of $r$ .
19M.2.SL.TZ2.T_3b:
Find the slant height of the cone-shaped container.
18N.1.SL.TZ0.T_1a:
Calculate the volume of this hemisphere in cm³.

Give your answer correct to one decimal place.
17M.1.SL.TZ1.T_9b:
Find the slant height, $l$ , of the cone.
20N.1.SL.TZ0.T_1b:
Calculate James’s estimate of its volume, in ${km}^{3}$ .
20N.1.SL.TZ0.T_1a:
Write down the value of the iron in the form $a \times 10^{k}$ where $1 \leq a < 10, k \in ℤ$ .
17M.2.SL.TZ1.T_4a:
Calculate the volume of this pan.
16N.2.SL.TZ0.T_6b:
Express this volume in ${\text{c}}{{\text{m}}^3}$ .
16N.2.SL.TZ0.T_6c:
Write down, in terms of $r$ and $h$ , an equation for the volume of this water container.
16N.2.SL.TZ0.T_6e:
Find $\frac{{{\text{d}}A}}{{{\text{d}}r}}$ .
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of $r$ which minimizes $A$ .
SPM.2.SL.TZ0.1a:
Find the volume of the sphere expressing your answer in the form $a \times {10^k}$ , $1 \leqslant a < 10$ and $k \in \mathbb{Z}$ .
18M.1.SL.TZ1.T_14a:
Calculate the radius of the base of the cone which has been removed.
20N.1.SL.TZ0.T_1c:
The actual volume of the asteroid is found to be $6.074 \times 10^{6} {km}^{3}$ .

Find the percentage error in James’s estimate of the volume.
18M.1.SL.TZ2.T_15b:
The total external surface area of the pencil case rounded to 3 significant figures is 570 cm².

Using your graphic display calculator, calculate the value of r.
21M.1.SL.TZ2.8c:
Find the value of $l$ .
17N.2.SL.TZ0.T_6b:
Calculate the radius, $r$ , of a hemisphere shaped glass.
18N.1.SL.TZ0.T_1c:
Write down your answer to part (b) in the form a × 10^k , where 1 ≤ a < 10 and k ∈ $\mathbb{Z}$ .
16N.1.SL.TZ0.T_7a:
Calculate the volume of the balloon.
19M.1.SL.TZ1.T_1c:
Find the volume, in cm³, of this calculator case.
18N.1.SL.TZ0.T_9b:
1 cm³ of glass has a mass of 2.56 grams.

Calculate the mass, in grams, of the paperweight.
17M.1.SL.TZ2.T_12b:
Find the value of $h$ .
17M.1.SL.TZ2.T_12a:
Find the volume of water in the container.
19M.1.SL.TZ1.T_15c:
Find the value of $r$ when the area of the curved surface is maximized.
18M.1.SL.TZ2.T_15a:
Find an expression for the slant height of the cone in terms of r.
17N.2.SL.TZ0.T_6a:
Show that the volume of a cone shaped glass is $160{\text{ c}}{{\text{m}}^3}$ , correct to 3 significant figures.
18M.1.SL.TZ1.T_14b:
Calculate the curved surface area of the cone which has been removed.
17M.2.SL.TZ1.T_4d:
Find the temperature that the pizza will be 5 minutes after it is taken out of the oven.
17M.1.SL.TZ1.T_9a:
Find the radius, $r$ , of the circular base of the cone.
18M.1.SL.TZ1.T_14c:
Calculate the curved surface area of the remaining solid.
18M.2.SL.TZ1.T_1e:
Show that Farmer Brown is incorrect.
17N.2.SL.TZ0.T_6d:
Show that there is $20{\text{ c}}{{\text{m}}^3}$ of orange paste in each special dessert.
16N.2.SL.TZ0.T_6d:
Show that $A = \pi {r^2} + \frac{{1\,000\,000}}{r}$ .
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
19M.1.SL.TZ1.T_15b:
Find $\frac{{{\text{d}}A}}{{{\text{d}}r}}$ .
18N.1.SL.TZ0.T_9a.ii:
Calculate the volume of the paperweight.
19M.2.SL.TZ1.T_2a:
Find the length ${\text{AB}}$ , giving your answer to four significant figures.
19M.2.SL.TZ1.T_2b:
Find the total area of the two rectangles that make up the roof.
19M.2.SL.TZ1.T_2d:
Find the percentage error in her estimate.
19M.2.SL.TZ1.T_2e:
Olivia investigates arranging the panels, such that the longer edge of each panel is parallel to ${\text{AB}}$ or ${\text{AC}}$ .

State whether this new arrangement will allow Olivia to fit more solar panels to the roof. Justify your answer.
17M.2.SL.TZ1.T_4b:
Find the radius of the sphere in cm, correct to one decimal place.
17M.2.SL.TZ1.T_4e:
Calculate, to the nearest second, the time since the pizza was taken out of the oven until it can be eaten.
16N.2.SL.TZ0.T_6a:
Write down a formula for $A$ , the surface area to be coated.
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
19M.2.SL.TZ2.T_3c:
Show that the total surface area of the cone-shaped container is 314 cm², correct to three significant figures.
19M.2.SL.TZ2.T_3d:
Find the height, $h$ , of this cylinder-shaped container.
19M.2.SL.TZ2.T_3a:
Find the volume of one cone-shaped container.
19M.2.SL.TZ2.T_3e:
The factory director wants to increase the volume of coconut water sold per container.

State whether or not they should replace the cone-shaped containers with cylinder‑shaped containers. Justify your conclusion.
18M.2.SL.TZ1.T_1a:
Calculate the area of triangle EAD.
18M.2.SL.TZ1.T_1b:
Calculate the total volume of the barn.
18M.2.SL.TZ1.T_1f:
Calculate the total length of metal required for one support.
17N.2.SL.TZ0.T_6e:
Find the total cost of the ingredients of one special dessert.

Hide related questions

Topic 3— Geometry and trigonometry

Prior learning

Question

Markscheme

Examiners report

Syllabus sections

View options