| Date | November 2016 | Marks available | 2 | Reference code | 16N.2.SL.TZ0.T_5 |
| Level | Standard Level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Calculate | Question number | T_5 | Adapted from | N/A |
Question
A farmer owns a plot of land in the shape of a quadrilateral ABCD.
and angle .
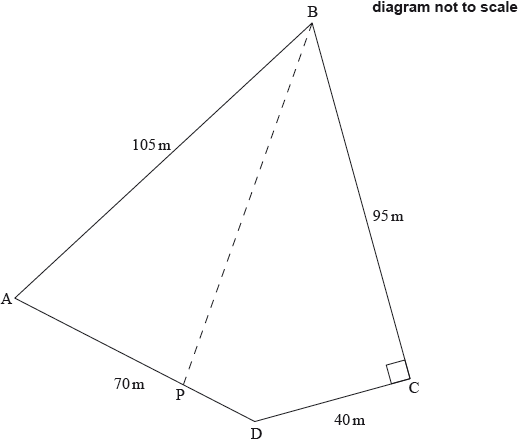
The farmer wants to divide the land into two equal areas. He builds a fence in a straight line from point B to point P on AD, so that the area of PAB is equal to the area of PBCD.
Calculate
the length of BD;
the size of angle DAB;
the area of triangle ABD;
the area of quadrilateral ABCD;
the length of AP;
the length of the fence, BP.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(M1)
Note: Award (M1) for correct substitution into Pythagoras’ theorem.
(A1)(G2)
[2 marks]
(M1)(A1)(ft)
Note: Award (M1) for substitution into cosine rule, (A1)(ft) for their correct substitutions. Follow through from part (a).
(A1)(ft)(G2)
Note: If their 103 used, the answer is
[3 marks]
(M1)(A1)(ft)
Notes: Award (M1) for substitution into the trig form of the area of a triangle formula.
Award (A1)(ft) for their correct substitutions.
Follow through from part (b).
If 68.8° is used the area .
(A1)(ft)(G2)
[3 marks]
(M1)
Note: Award (M1) for correctly substituted area of triangle formula added to their answer to part (c).
(A1)(ft)(G2)
[2 marks]
(M1)(M1)
Notes: Award (M1) for the correct substitution into triangle formula.
Award (M1) for equating their triangle area to half their part (d).
(A1)(ft)(G2)
Notes: Follow through from parts (b) and (d).
[3 marks]
(M1)(A1)(ft)
Notes: Award (M1) for substituted cosine rule formula.
Award (A1)(ft) for their correct substitutions. Accept the exact fraction in place of .
Follow through from parts (b) and (e).
(A1)(ft)(G2)
Notes: If 54.4 and are used the answer is
[3 marks]




