| Date | November 2017 | Marks available | 2 | Reference code | 17N.2.SL.TZ0.S_10 |
| Level | Standard Level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Show that | Question number | S_10 | Adapted from | N/A |
Question
Note: In this question, distance is in millimetres.
Let , for .
The graph of passes through the origin. Let be any point on the graph of with -coordinate , where . A straight line passes through all the points .
Diagram 1 shows a saw. The length of the toothed edge is the distance AB.
The toothed edge of the saw can be modelled using the graph of and the line . Diagram 2 represents this model.
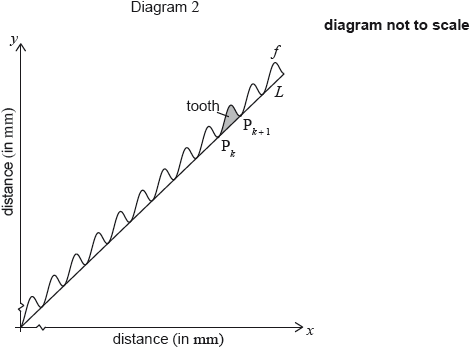
The shaded part on the graph is called a tooth. A tooth is represented by the region enclosed by the graph of and the line , between and .
Show that .
Find the coordinates of and of .
Find the equation of .
Show that the distance between the -coordinates of and is .
A saw has a toothed edge which is 300 mm long. Find the number of complete teeth on this saw.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
substituting M1
eg
(A1)
A1
AG N0
[3 marks]
substituting the value of (M1)
A1A1 N3
[3 marks]
attempt to find the gradient (M1)
eg
correct working (A1)
eg
y = x A1 N3
[3 marks]
subtracting -coordinates of and (in any order) (M1)
eg
correct working (must be in correct order) A1
eg
distance is AG N0
[2 marks]
METHOD 1
recognizing the toothed-edge as the hypotenuse (M1)
eg, sketch
correct working (using their equation of (A1)
eg
(exact), 212.132 (A1)
dividing their value of by (M1)
eg
33.7618 (A1)
33 (teeth) A1 N2
METHOD 2
vertical distance of a tooth is (may be seen anywhere) (A1)
attempt to find the hypotenuse for one tooth (M1)
eg
(exact), 8.88576 (A1)
dividing 300 by their value of (M1)
eg
33.7618 (A1)
33 (teeth) A1 N2
[6 marks]

