12.1 Electrons in atoms
Written specifically for students to provide help and support for the IB Diploma chemistry programme this page provides full coverage of the syllabus content of Topic 12.1 Electrons in atoms. It encourages you to think critically and provides many questions with full worked answers so that you can monitor and improve your knowledge and understanding.

 Learning outcomes
Learning outcomes
After studying this topic you should be able to:
 Understand:
Understand:
- The limit of convergence at higher frequency in an emission spectrum corresponds to the first ionization energy
- Evidence for the existence of main energy levels and sub-levels in atoms comes can be found in the trends in first ionization energy across periods.
- Explain how the lines in the emission spectrum of hydrogen are related to electron energy levels.
- Data from the successive ionization energies of elements provides information relating to electron configurations.
Apply your knowledge to:
- Use the wavelength or frequency of the convergence limit obtained from emission spectral data to calculate the value of the first ionization energy.
- Deduce the group of an element from its successive ionization data.
- Explain the trends and discontinuities in first ionization energies across a period.
Relationships & vocabulary
Nature of Science
The fact that evidence for the existence of energy levels comes from emission spectra provides a good example that theories are supported by experimental evidence.
International-mindedness
Two separate international teams working at CERN on the Large Hadron Collider independently published in 2012 that they had discovered a particle with properties consistent with those previously predicted for the ‘Higgs boson’ particle.
For examples and more links to International mindedness, Theory of knowledge, utilization etc. see separate page which covers all of Topics 2 & 12: The nuclear atom.
Vocabulary
| ionization energy | discharge tube | line spectrum |
| continuous spectrum | convergent | Planck's constant |
Learning slides
You can use this slide gallery for learning or for reviewing concepts and information. It covers all the key points in the syllabus for this sub-topic.
Something to think about

Hydrogen gas discharge tube
Each element has a unique atomic spectrum which consists of discrete lines and is therefore not continuous. The simplest element, hydrogen has lines in the visible region at wavelengths of 656 nm, 486 nm, 434 nm 410 nm etc. which converge at the higher energy end of the spectrum at 365 nm.
These lines are governed by a simple mathematical relationship: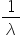 = R (
= R (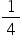 −
− 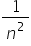 ) where n = 3 (to give 656 nm), 4 (to give 486 nm), 5,6….. etc. R is known as the Rydberg constant.
) where n = 3 (to give 656 nm), 4 (to give 486 nm), 5,6….. etc. R is known as the Rydberg constant.
It can be seen that as 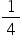 is also
is also 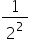 this equation is a special case of a more general equation:
this equation is a special case of a more general equation: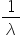 = R (
= R ( 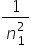 −
− 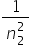 ) where n1 = 1, 2, 3, 4….. and n2 = (n1+1), (n1+2), (n1+3), (n1+4)……
) where n1 = 1, 2, 3, 4….. and n2 = (n1+1), (n1+2), (n1+3), (n1+4)……
If n1 = 1 then the series of lines will be of higher energy (shorter wavelength) and appear in the ultraviolet region of the spectrum. n1 = 2 gives the lines in the visible region and n1 =3 will give a series of lines in the infra-red region etc. (This is a nice example of a deduction made from an observation as only the lines in the visible spectrum can be seen with the naked eye.)
For emission spectra these series of lines represent electrons falling from higher to lower energy levels.
Evidence that they do relate to the energy levels that can be occupied by the electron can be obtained by considering promoting an electron from the lowest possible energy level to infinity, i.e. removing the electron completely, in other words ionizing the atom. In this case n1= 1 and n2 = infinity.
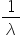 = R (
= R (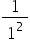 −
− 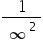 ) so that
) so that 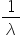 = R. Since c = λv and E= hv then
= R. Since c = λv and E= hv then
E = hcR for one electron or hcRL for one mole of electrons.
Planck’s constant (h), the velocity of light (c), Rydberg’s constant (R) and Avogadro's constant (L) are four of the most accurately known constants in science. By substituting their values into this theoretically derived equation we can calculate the energy required to remove one electron from a mole of gaseous hydrogen atoms i.e. the ionization energy.
E = (6.6261 x 10−34 Js) x (2.9980 x 108 ms−1) x (1.0974 x 107 m−1) x (6.0221 x 1023 mol−1)
= 1.313 x 106 J mol−1 = 1313 kJ mol−1 which agrees completely with the experimentally determined value given in Section 8 of the IB data booklet (1312 kJ mol−1).This provides strong evidence that atomic spectra are due to electron transitions between energy levels within the atom.
Although the above calculation shows that the emission spectrum of hydrogen does very much support the Bohr model of the atom, Higher Level students do not have to use the Rydberg equation in calculations. You can obtain the ionization energy of hydrogen directly from the fact that the convergence line in the ultraviolet appears at a wavelength of 9.12 x 10−8 m.
E = hv = 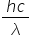 =
= 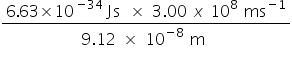 = 2.18 x 10−18J (for one electron)
= 2.18 x 10−18J (for one electron)
= 2.18 x 10−18 J x 6.02 x 1023 mol−1 = 1.31 x 106 J mol−1 = 1310 kJ mol−1 (to 3 SF)
Test your understanding of this topic
(Note that your teacher may have restricted your access to some or all of these questions and worked answers if they are going to use them as a class test or set them as an assignment.)
For ten 'quiz' multiple choice questions with the answers explained see MC test: Electrons in atoms.
For short-answer questions see Electrons in atoms questions.
More resources
1. If you like simulations then you could try this one called Hydrogen atom simulator ![]() from the University of Nebraska-Lincoln. Be warned though that it uses electron volts as the unit of energy!
from the University of Nebraska-Lincoln. Be warned though that it uses electron volts as the unit of energy!
2. Using a diffraction grating to show how four different elements can be identified from their emission spectra.

 IB Docs (2) Team
IB Docs (2) Team 










