Topic 1

Including International-mindedness, TOK, and 'Utilization' in Stoichiometric relationships

International-mindedness

Many of the references to International-mindedness for Topic 1 relate to the international bodies responsible for the correct use of units (SI system and BIPM) and the naming of compounds (IUPAC). This enables chemists to use a common language which is universally understood.

1. The SI system of units

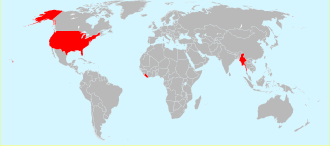There are clearly several different commonly used units used for measuring temperature. This is still true for other measurements of quantities too. In the United States temperature is still measured in degrees Fahrenheit and petrol (well actually gasoline) is bought in US gallons (which are different to UK gallons). Even in the UK, which has more or less gone metric and where they do now buy petrol in litres (but not dm3), they still buy a pint of beer in the pub and measure the speed of their car in miles per hour. It was Napoleon Bonaparte who introduced metric units (with help from Lavoisier) and the system became known as Le Système international d'unités. If scientists are going to cooperate internationally then they do need to be using the same units to measure quantities. In 1960 the International System of Units (SI) was adopted by almost all countries although some continue to use their own historical units (such as the pint and the mile) alongside SI units. The only three countries that have not officially adopted SI units are the USA, Liberia and Myanmar (Burma).

The use of SI units can bring some rather strange units to chemistry. Perhaps one of the hardest for our students to grasp is the use of decimetres cubed for volume. Since the SI unit of length is the metre then volume has the SI units metres cubed. A litre is 1 x 10-3 m3 or 1 dm3. In the IB we do use dm3 for a litre but in many countries (e.g. France) they still express concentration in mol l-1 rather than mol dm-3. One unit that is almost universal for chemists is the mol but then in some countries M is used, rather than mol dm-3, for concentration.

  2. International Bureau of Weights and Measures (BIPM)

The International Bureau of Weights and Measures (BIPM) has an international staff of over 70 and is based near Paris in France. Its role is to provide a single, coherent system of measurements throughout the world related to the International System of Units. This takes many forms, for example, the coordination of national measurement standards. It also provides a calibration and measurement service.

   3. IUPAC

In 1919 the International Union of Pure and Applied Chemists (IUPAC) was formed. IUPAC is an international, non-governmental body made up of chemists from both academia and industry. The aim of IUPAC is to foster worldwide communication in chemistry. Currently about one thousand chemists throughout the world are engaged on a voluntary basis working for IUPAC. For more detailed information on the importance of IUPAC see the page on IUPAC on Language of Chemistry in the TOK section.

4. Law of constant composition

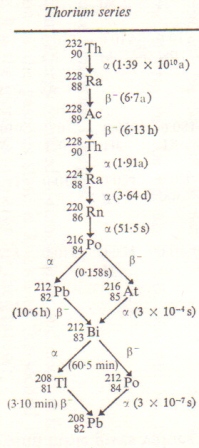Perhaps the most obvious way of all in which chemistry is international is that the formula of a pure compound is the same no matter how it is made or where in the world it is found – that is, the mass of each element in one mole of the compound will be constant. This is technically known as the Law of Constant Composition (sometimes known as the law of Definite Proportions). It is true in virtually all cases but there are a few exceptional cases where it is not exactly true. For example the atomic mass of lead is given as 207.19 g mol-1 in the IB Data Booklet. Lead(II) oxide has the formula PbO so one would expect that one mole of any sample of lead(II) oxide found anywhere in the world would contain exactly 16.00 g of oxygen and 207.19 g of lead. This is not true because the atomic mass of lead is the weighted average mass of all the naturally occurring isotopes. The isotopic composition of lead can vary depending on its surroundings as it is the decay product of heavy radioactive elements. If there is uranium-238 in the rocks the lead will be richer in Pb-206 whereas if the lead has been formed from the decay of thorium-232 the lead will be richer in Pb-208 and the relative atomic mass will be slightly higher. This used to be classed as nitpicking in the extreme and essentially chemical compounds very definitely can be thought to fit the ‘International Dimension’ box. However a recent paper in December 2010 produced by IUPAC has now listed ten common elements (including hydrogen, carbon and oxygen) where the relative atomic mass is no longer given as a fixed number but as a range to account for the variations in naturally occurring stable isotopes depending upon the source of the element. You can read further about this in my blog on Atomic masses change.

Theory of Knowledge

Among the references to TOK listed in Topic 1 are the magnitude of Avogadro’s constant which is beyond the scale of everyday experience; whether the use of a universal language in chemistry increases or hinders understanding and why mathematics is effective in describing the natural world.

   1. Can there be such a thing as ‘nothing’?

“Nature abhors a vacuum”

According to an internet search this quotation has been variously attributed to Spinoza, Descartes, Rabelais and Tennessee Williams but it seems most likely to originate from Aristotle – the origin of quotations could form a TOK question in itself? This quotation is perhaps more often used in the political sense rather than in its literally scientific context.

The size of Avogadro’s constant is mind-boggling and probably beyond our everyday comprehension and I have produced a powerpoint illustrating how this concept could be covered with students. When teaching the gas laws It is worth applying the concept of Avogadro’s constant to consider whether the perfect vacuum, i.e. nothing, can ever exist.

Horses trying to pull apart two evacuated bronze spheres in Magdeburg, Germany in 1657. The experiment was performed by Otto von Guericke

The molar volume of a gas (1.3) means that one mole of a perfect gas will occupy 22.7 dm3 at 273 K and 100 kPa pressure. This means that at 0 oC one litre of a gas such as oxygen will contain approximately 0.045 mol, that is approximately 2.7 x 1022 molecules, of oxygen when the pressure is 100 kPa. We can easily envisage one litre but it is hard to envisage 2.7 x 1022 individual molecules. If we reduce the pressure to 10 kPa (approximately 0.1 atmosphere) then the number falls to 2.7 x 1021 molecules of oxygen etc... A typical vacuum pump is advertised as being able to reach a pressure as low as 0.4 mbar. If my physics is correct then 1 bar = 100,000 Pa (Nm-2) = 0.98692 atmosphere. This means that 0.4 mbar is approximately equal to 4 x 10-5 atm. If I use this vacuum pump to pump ‘all’ the oxygen out of my one litre container then I will have a pressure of 4 x 10-5 atm which means I will still have approximately 2.4 x 1019 molecules in my container. That is still an awful lot of molecules. Maybe you can buy a vacuum pump that is even more powerful but you can see that however good the pump it will never be able to remove all the oxygen molecules. In fact it is impossible to obtain a vacuum because the vapour pressure of the material of the container would ensure that some of the molecules of the container would exist in the gaseous state. I think this is quite a strong argument for the fact that ‘nothing’ can never exist? We can never have an empty container.

It is rather like the alchemists who searched for the universal solvent. They could never have found it as it would have dissolved whatever it was contained in.

   2. Measurement of temperature

A few years ago an exam question asked students to explain the difference between temperature and heat. It was surprising how many were unable to answer the question correctly. Heat is a form of energy and has the SI units (see above) of Joules (or kJ). Temperature is a measure of the ‘hotness’ of something. 100 cm3 of water at 50 oC has twice as much heat as 50 cm3 of water at 50 oC but both have the same temperature.

As well as degrees Celsius (oC) there are various other scales to measure temperature. These include degrees centigrade (oC), degrees Fahrenheit (oF) and Kelvin (K). Scales of temperature initially developed in the same way as other units (such as for time or for length or mass). They are essentially practical units based on human experience. For example a furlong was originally the length a team of oxen could plough without resting. For temperature water was used as the reference. The German physicist Daniel Gabriel Fahrenheit (1686–1736) devised the Fahrenheit scale based on the boiling point of water (212 oF), the temperature under his wife’s armpit (96 oF), the freezing point of brine (oF) and the freezing point of pure water (32 oF). In an attempt to bring a more rational system of numbers into the measurement, the difference between the boiling point and freezing point of pure water was then divided into one hundred equal units giving degrees centigrade. This was first suggested by a Swedish astronomer, Anders Celsius (1701-1744), and since 1948 degrees centigrade are more correctly referred to as degrees Celsius.

There is really only one natural scale of temperature and that starts at absolute zero. It is impossible (according to the Third Law of Thermodynamics) to go below absolute zero as at this temperature there would be no motion left in the whole universe. However the intervals of temperature using this scale are still the same as degrees Celsius so that the freezing point of water is 273 K (actually 273.15 K) and the boiling point at 1 atmosphere pressure is 373.15 K. In a sense we have an absolute scale divided into artificial units based on water!

It can cause an interesting conundrum when it comes to uncertainty and how many significant figures to quote when you measure temperature. Suppose a student measures the temperature of a gas to be 20.0 oC using a thermometer that has an accuracy of ± 0.5 oC. 20.0 is three significant figures and the uncertainty is (100 x 0.5/20) which comes to 2.5%. If the student needs to use this value in the ideal gas equation then he or she has to convert it into Kelvin. It now becomes 293.0 K ± 0.5 K. Using the same thermometer the number of significant figures has changed to four and the uncertainty has changed to (100 x 0.5/293) = 0.17%. Which is correct?

Utilization

Specific references to utilization include refrigeration and the freeze drying of food as examples of changes of state. The importance of stoichiometric calculations, percentage yield and the atom economy in industry is stressed. The rapid gas-volume changes in air bags is also listed.

  1. Inflating an air bag

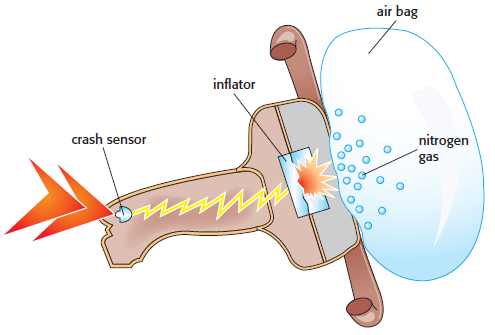
Some reactions proceed very fast, whereas others can proceed so slowly that it can take millions of years before any appreciable amount of products are formed. An example of a very fast reaction that we have come to rely on is the rapid inflation of airbags used in automobiles. Typical reactants are a mixture of sodium azide (NaN3), potassium nitrate (KNO3) and silicon dioxide. The sodium azide and the potassium nitrate react to produce inert nitrogen gas, which inflates the bag:

10NaN3(s) + 2KNO3(s) → K2O(s) + 5Na2O(s) + 16N2(g)

The silicon dioxide is present to convert the oxides of potassium and sodium that are produced into harmless silicates. When a crash occurs, a sensor in the car’s airbag will trigger the reaction if the driver (and passengers) continues to move forward with a momentum greater than the equivalent of hitting a brick wall at 16–24 km h–1. The nitrogen has to be produced to inflate the bag more quickly than the time taken for the driver to hit the steering wheel. The whole reaction from triggering to complete inflation of the bag is complete in less than one 25th. of a second.

  2. Determining a 'safe limit'

Both social and economic aspects can be addressed in how we express ‘safe limits’. Topic 1.1 deals with concentration which chemists usually express in mol dm-3 but there are other common units such as parts per million (ppm). The general public looks to chemists and other scientists to determine what are ‘safe limits’ for a whole range of different chemicals. For example Californian State legislation sets the ‘safe limit’ of fluoride ions in drinking water at 2 ppm, and the current World Health Guideline for nitrogen dioxide in the atmosphere is an annual mean of 40 micrograms per cubic metre.

The problem is that often the only truly safe limit for many substances is zero. Pregnant women are often told this in relation to alcohol. This may be fine for alcohol where humans generally have control over how much they consume but many other ‘safe limits’ have to be put into context with amounts that are naturally present. Safe limits are sometimes based on research but more often they are very subjective and can be altered by political and economic factors. Volcanic ash prevented many aeroplanes from flying in the summer of 2010 during the eruption of the Eyjafjallajökull volcano in Iceland. Airlines and the economy were severely affected and it was not long before the ‘safe limit’ was altered to allow aircraft to fly again even though the levels of ash had not changed significantly.

Chemists can measure the concentrations of potential pollutants or harmful materials but deciding how much is ‘safe’ is often beyond the remit of chemists.

All materials on this website are for the exclusive use of teachers and students at subscribing schools for the period of their subscription. Any unauthorised copying or posting of materials on other websites is an infringement of our copyright and could result in your account being blocked and legal action being taken against you.