Activation energy questions

Assignment: Questions on Topic 16.2: Activation energy

This page of questions can be marked as direct student access either for assigning as a test or for students to work on in their own time. If you do not wish to use student access, links to downloadable versions of the questions and, separately the worked answers, can be found at Printable versions of written tasks.

1

At a temperature of 700 K the rate constant for the redox reaction between nitrogen(IV) oxide and carbon monoxide is 1.30 mol−1 dm3 s−1.

NO2(g) + CO(g)→ NO(g) + CO2(g) k = 1.30 mol−1 dm3 s−1 at 700 K

i.   Deduce the overall order of this reaction.

1 line
Show model answer
(Students can only see the model answer after they have submitted the task)

ii.  The activation energy is 133.8 kJ mol−1.
Determine the temperature when the rate constant for the reaction will be 20.0 mol−1 dm3 s−1.

10 lines
Show model answer
(Students can only see the model answer after they have submitted the task)
2

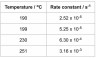
In the gas phase methyl isocyanide, H3CNC, rearranges to form ethanenitrile, H3CCN.

The table below shows the experimentally determined values of the rate constant for this rearrangement at different temperatures.

i.   Determine the overall order of the reaction.

1 line
Show model answer
(Students can only see the model answer after they have submitted the task)

ii.  Write the rate expression for the reaction.

1 line
Show model answer
(Students can only see the model answer after they have submitted the task)

iii.  Using a graphical method, determine the activation energy for the rearrangement of methyl isocyanide.

10 lines
Show model answer
(Students can only see the model answer after they have submitted the task)

iv.  Determine the value of the rate constant for this reaction at (I) 210 oC and (II) 283 oC.

2 lines
Show model answer
(Students can only see the model answer after they have submitted the task)
All materials on this website are for the exclusive use of teachers and students at subscribing schools for the period of their subscription. Any unauthorised copying or posting of materials on other websites is an infringement of our copyright and could result in your account being blocked and legal action being taken against you.