12.1 The Interaction of Matter with Radiation

When monochromatic light is incident on a clean metal surface, photoelectrons may be emitted through the photoelectric effect. 

For monochromatic light of wavelength 570 nm a stopping potential of 1.80 V is required for this particular metal surface. 

The wave function of Schrödinger's theory can be thought of as a generalisation of the de Broglie hypothesis. 

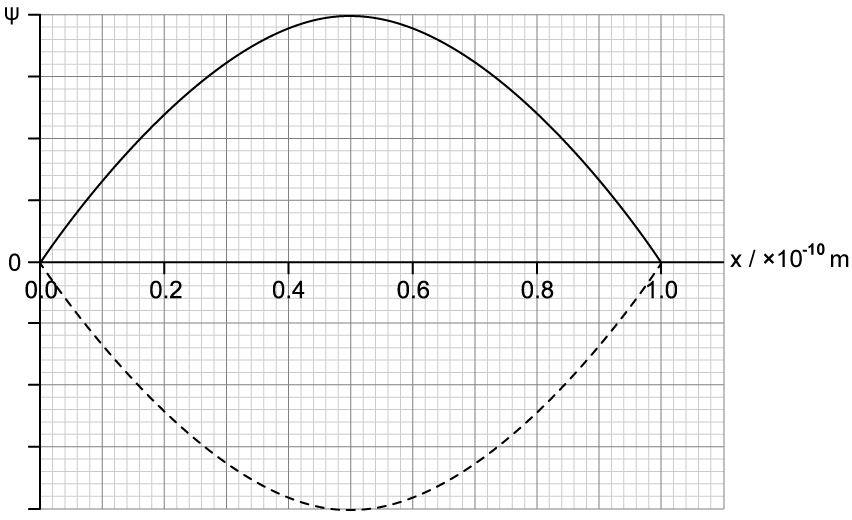
The wave function ψ for an electron confined to length 1.0 × 10^–10 m is a standing wave as shown. 

[2]

One of the striking features of quantum theory is the ability of nature to convert matter into energy and vice versa. 

Imagine an electron moving with kinetic energy E_k on a collision course with a positron moving in the opposite direction with the same kinetic energy. Following annihilation, two photons are produced. 

Monochromatic light is incident on a metal surface and electrons are emitted instantaneously from the surface. 

The wavelength of light incident in part (a) is 450 nm and the work function of the metal is 2.0 × 10^–19 J. 

The light source used in part (b) is now incident on a different metal surface. Its frequency is varied, such that the kinetic energy of emitted electrons can be recorded.  

The graph shows how the maximum kinetic energy E_K of the ejected electrons varies with the frequency of incident light.