Question 1a

Marks: 2

(a)

Outline why the gravitational potential is negative everywhere in space.

[2]

Key Concepts

Potential & Potential Energy

Question 1b

Marks: 2

The gravitational potential of the Sun at its surface is V is –1.9 x 10¹¹ J kg^–1 at a radial distance r from its core.

The following data are available:

Mass of Earth = 6.0 × 10²⁴ kg
Distance from Earth to Sun = 1.5 × 10¹¹ m
Radius of Sun = 7.0 × 10⁸ m

(b)

Calculate the Earth's gravitational potential energy in its orbit around the Sun.

[2]

Key Concepts

Potential Energy Calculations

Question 1c

Marks: 2

(c)

While the Earth orbits the Sun, terrestrial shuttles often enter orbit around Earth. One such shuttle is launched with a kinetic energy E_K given by the expression below:

E_{K} = \frac{5 G M_{E} m}{8 R_{E}}

where G is the gravitational constant, M_E is the mass of Earth, and m is the mass of the shuttle. Deduce that the shuttle cannot escape the gravitational field of the Earth.

[2]

Key Concepts

Orbital Energy Calculations
Orbital Motion, Speed & Energy

Question 1d

Marks: 3

(d)

Show that, if the shuttle enters an orbit of radius R about the Earth, then its total energy is given by

- \frac{G M_{E} m}{2 R}

stating an appropriate assumption required.

[3]

Key Concepts

Orbital Motion, Speed & Energy
Orbital Energy Calculations

Question 2a

Marks: 2

(a)

Evaluate this statement of Newton's law of gravitation: "The gravitational force between two masses is proportional to the masses and inversely proportional to the square of the distance between them."

[2]

Key Concepts

Forces & Inverse-Square Law Behaviour

Question 2b

Marks: 3

(b)

A satellite of mass m orbits a planet of mass M. If the orbital radius is R and the orbital period is T, show that the ratio

\frac{R^{3}}{T^{2}}

is constant.

[3]

Key Concepts

Forces & Inverse-Square Law Behaviour
Orbital Motion, Speed & Energy

Question 2c

Marks: 3

(c)

Calculate the change in gravitational potential energy of the satellite, of mass 39 kg, as it moves from an orbit of height 1100 km above the Earth's surface to one of height 2100 km.

Use the following data:

Mass of Earth = 6.0 × 10²⁴ kg
Average radius of Earth = 6.4 × 10⁶ m

[3]

Key Concepts

Potential Difference
Potential & Potential Energy

Question 2d

Marks: 2

(d)

Explain whether the gravitational potential energy has increased, decreased or stayed the same when the orbit changes as in part (c).

[2]

Key Concepts

Potential & Potential Energy
Potential Difference

Question 3a

Marks: 2

(a)

Define electric potential at a point in an electric field.

[2]

Key Concepts

Potential & Potential Energy

Question 3b

Marks: 5

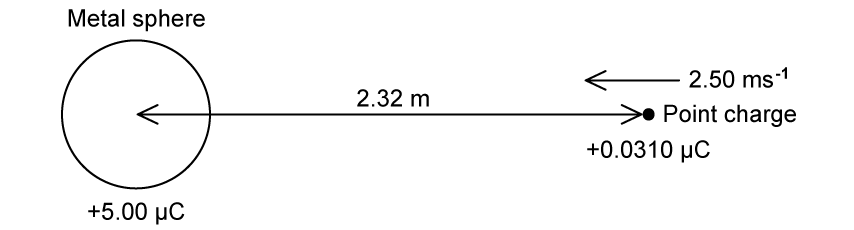
A point charge of mass 1.30 × 10^–4 kg is moving radially towards a small, charged metal sphere as shown.

10-2-hl-sq-medium-q3b

(b)

The electric potential at the surface of the sphere is 9.00 × 10⁴ V. Determine if the point charge will collide with the metal sphere.

[5]

Key Concepts

Potential & Potential Energy
Potential in a Charged Sphere

Question 3c

Marks: 2

(c)

Determine the speed at which the point charge is certain to collide with the metal sphere.

[2]

Key Concepts

Potential Difference

Question 3d

Marks: 4

Protons are positively charged and are often described as "colliding" in particle accelerator experiments, as well as in the core of stars.

(d)

Discuss the implications of two protons colliding in terms of the forces between them. Describe the conditions necessary for such a collision to take place.

[4]

Key Concepts

Forces & Inverse-Square Law Behaviour
Forces on Charges & Masses

Question 4a

Marks: 2

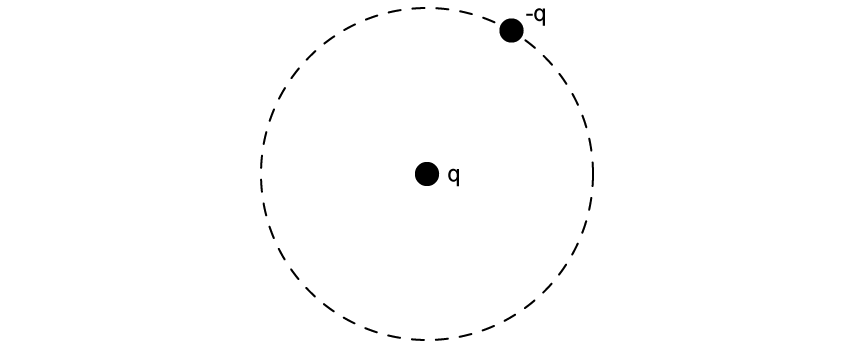
A charge –q with mass m orbits a stationary charge q with a constant orbital radius r.

10-2-hl-sq-medium-q4a

(a)

Draw the electrostatic force on –q due to the electric field created by q.

[2]

Key Concepts

Forces & Inverse-Square Law Behaviour

Question 4b

Marks: 2

(b)

Show that the orbital speed of v is given by:

v = \sqrt{\frac{1}{4 π ε_{0} m r}} q

[2]

Key Concepts

Orbital Motion, Speed & Energy

Question 4c

Marks: 3

(c)

Show that the total energy E of the orbiting charge is given by:

$E = - \frac{1}{8 π ε_{0}} \frac{q^{2}}{r}$

[3]

Key Concepts

Orbital Energy Calculations
Orbital Motion, Speed & Energy

Question 4d

Marks: 2

(d)

Hence, determine an equation for how much energy must be supplied to –q if it is to orbit the stationary charge q at twice the radius in part (c), 2r.

[2]

Key Concepts

Orbital Energy Calculations
Potential & Potential Energy

Question 5a

Marks: 3

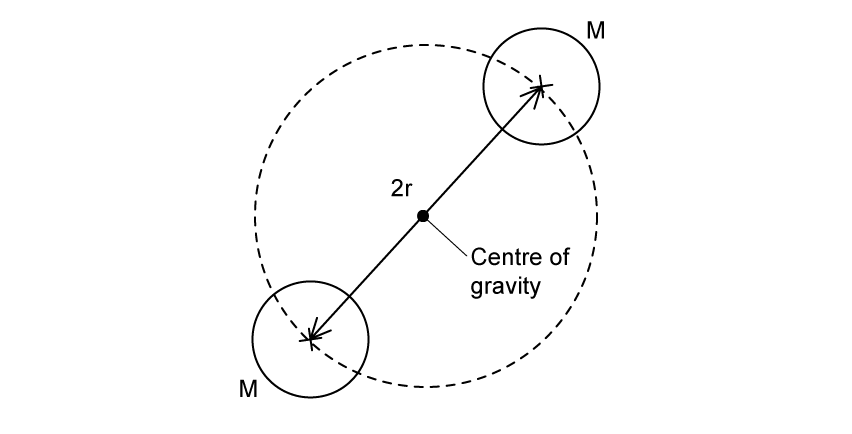
Binary star systems involve two stars that orbit a common centre of gravity. One such system is shown.

10-2-hl-sq-medium-q5a

Each star has a mass M and orbital radius r, such that their separation is 2r.

(a)

Deduce that the time period T of each star's orbit is related to the orbital radius r by the following equation:

T^{2} = \frac{16 π^{2} r^{3}}{G M}

[3]

Key Concepts

Orbital Motion, Speed & Energy
Forces & Inverse-Square Law Behaviour

Question 5b

Marks: 2

(b)

Show that the kinetic energy of each star in the binary system is given by:

E_{K} = \frac{G M^{2}}{8 r}

[2]

Key Concepts

Orbital Motion, Speed & Energy

Question 5c

Marks: 2

(c)

Hence, show that the total energy of the binary star system is given by the equation:

E = - \frac{G M^{2}}{4 r}

[2]

Key Concepts

Orbital Motion, Speed & Energy
Orbital Energy Calculations

Question 5d

Marks: 3

The binary system radiates energy in the form of gravitational waves.

(d)

Deduce that the stars move closer to each other as the binary system emits gravitational waves.

[3]

Key Concepts

Orbital Motion, Speed & Energy

DP IB Physics: HL

Topic Questions

10.2 Fields at Work

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Resources

Members

Company

Quick Links