Question 1a
A ball within a ball-spring system oscillates about an equilibrium point.
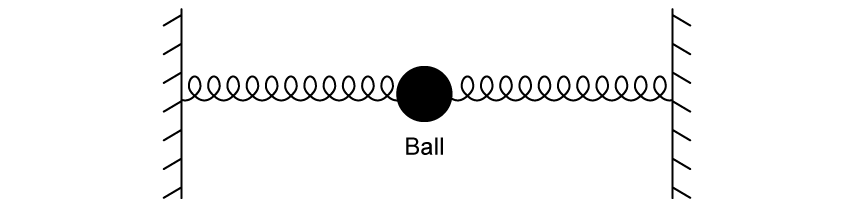
[2]
Question 1b
The ball is oscillating in simple harmonic motion. The graph shows the displacement of the ball over time.
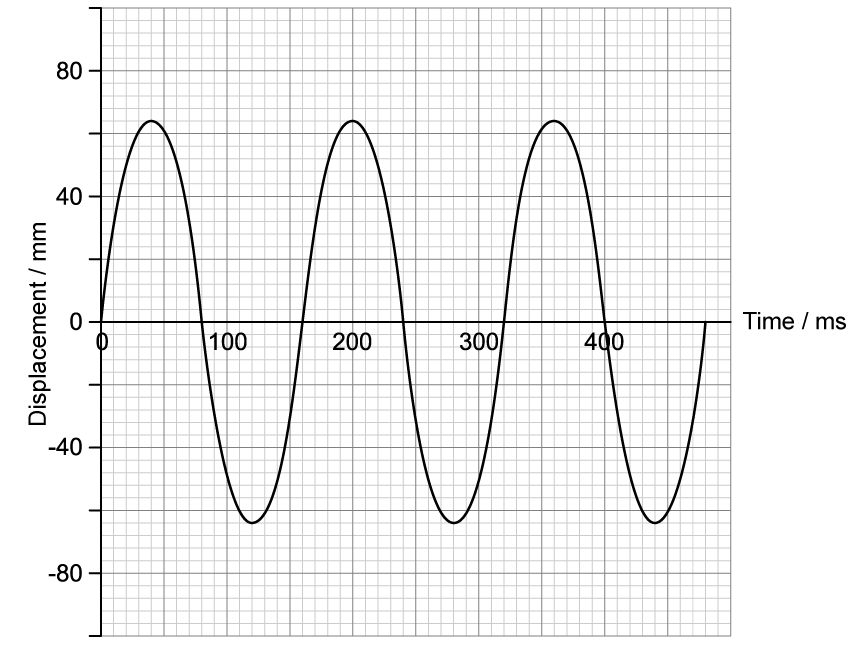
[2]
Question 1c
[1]
Question 1d

A ball within a ball-spring system oscillates about an equilibrium point.

[2]
The ball is oscillating in simple harmonic motion. The graph shows the displacement of the ball over time.

[2]
[1]

[4]
[3]
The investigation from part (a) is repeated. The same wooden block and spring are used, but a second identical spring is added in parallel.
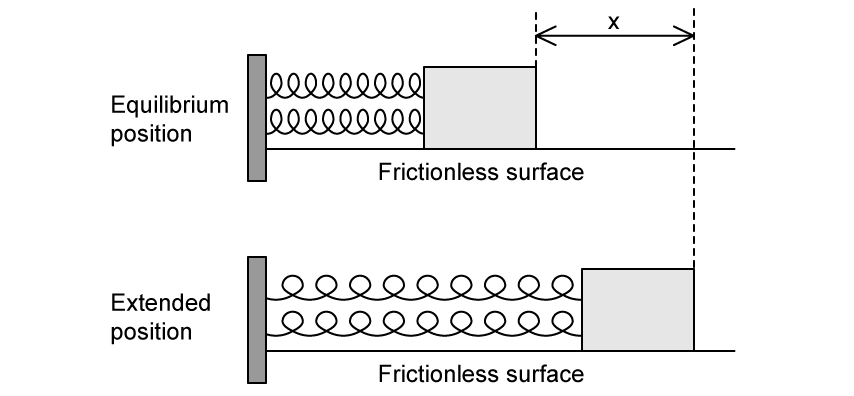
[3]
The spring from part (a) is attached to the mass in part (a), and oscillates freely in simple harmonic motion.
The graph shows the variation of displacement with time t of the mass on the spring.

[2]
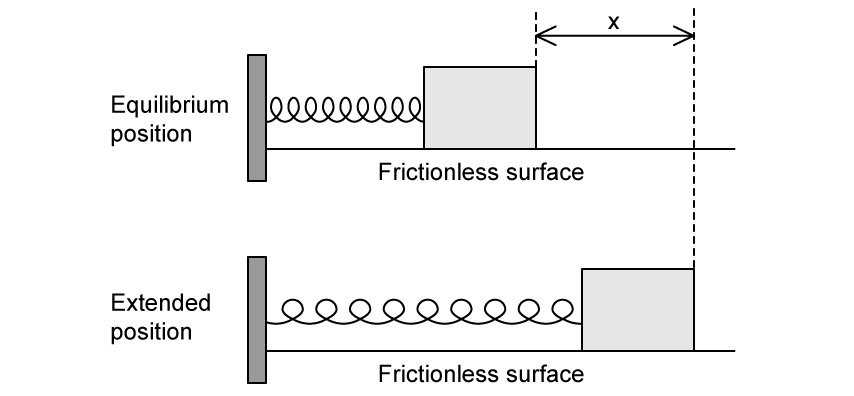
A mass of 75 g is connected between two identical springs. The mass-spring system rests on a frictionless surface. A force of 0.025 N is needed to compress or extend the spring by 1.0 mm.
The mass is pulled from its equilibrium position to the right by 0.055 m and then released. The mass oscillates about the equilibrium position in simple harmonic motion.
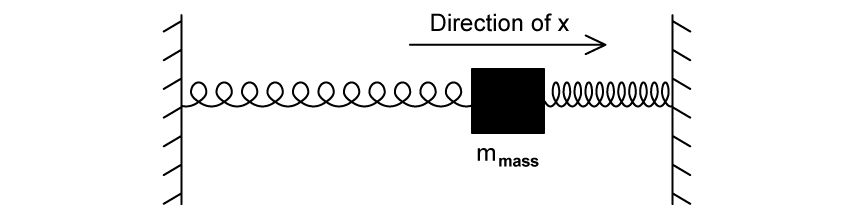
The mass-spring system can be used to model the motion of an ion in a crystal lattice structure.
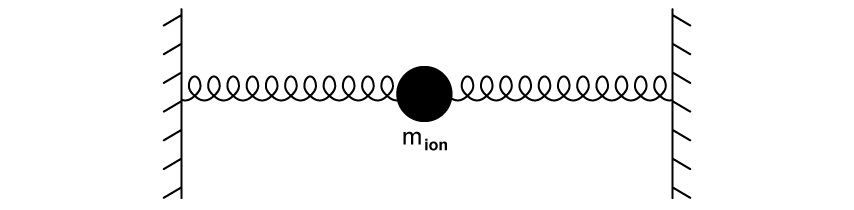
The frequency of the oscillation of the ion is 8 × 1012 Hz and the mass of the ion is 6 × 10−26 kg. The amplitude of the vibration of the ion is 2 × 10−11 m.
[1]
(ii) Estimate the maximum kinetic energy of the ion.
[1]
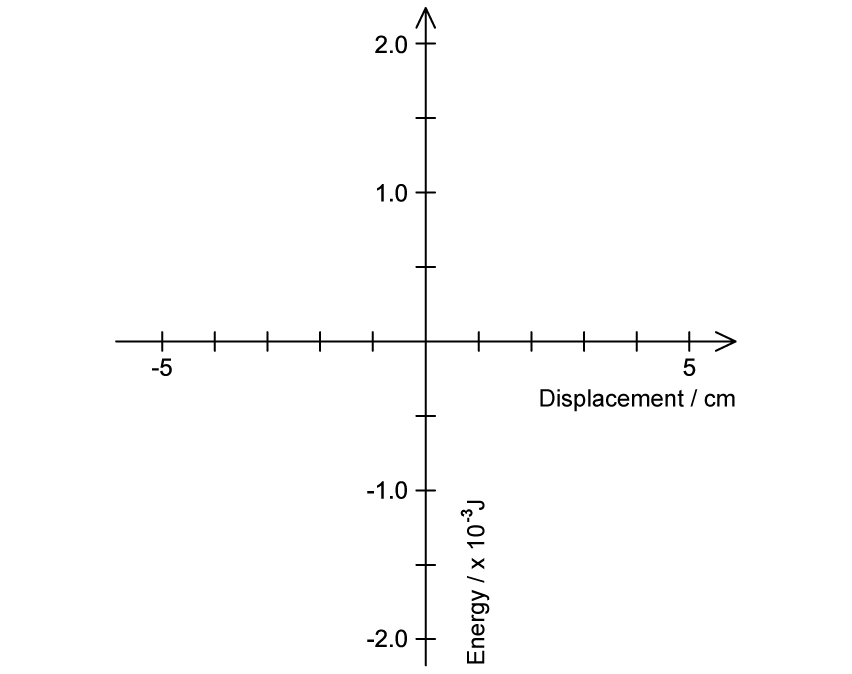
Use the axes to sketch a graph showing the variation over time of the kinetic energy of the mass and the potential energy of the springs.
You should include appropriate values, and show the oscillation over one full period.

[2]
The same mass and a single spring from part (a) are attached to a rigid horizontal support.

The length of the spring with the mass attached is 64 mm. The mass is pulled downwards until the length of the spring is 76 mm. The mass is released, and the vertical mass-spring system performs simple harmonic motion.
[2]
The diagram shows the vertical spring-mass system as it moves through one period.

Annotate the diagram to show when:
Ep = max
Ek = max
v = 0
v = max
[2]
A ball is displaced through a small distance x from the bottom of a bowl and then released.
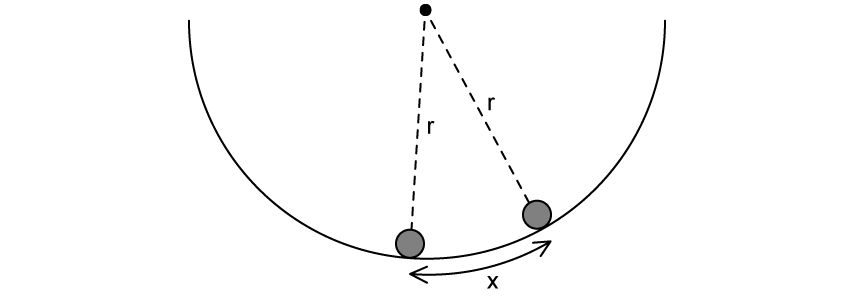
The frequency of the resulting oscillation is 1.5 Hz and the maximum velocity reaches 0.36 m s−1. r is the radius of the bowl.
[1]
[1]
[4]
The ball was replaced by a ball of the same size, but with a greater mass.
[2]
An experiment is carried out on Planet Z using a simple pendulum and a mass-spring system. The block moves horizontally on a frictionless surface. A motion sensor is placed above the equilibrium position of the block which lights up every time the block passes it.
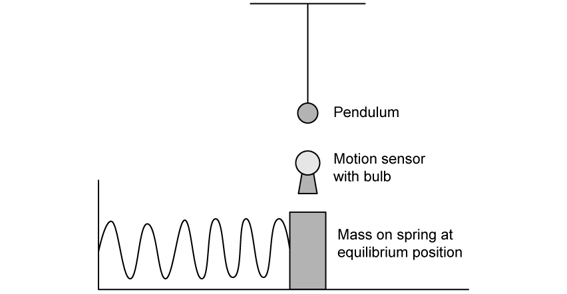
The pendulum and the block are displaced from their equilibrium positions and oscillate with simple harmonic motion. The pendulum bob completes 150 full oscillations in seven minutes and the bulb lights up once every 0.70 seconds. The block has a mass of 349 g.
[2]
The volume of Planet Z is the same as the volume of Earth, but Planet Z is twice as dense.
[2]
The angle that the pendulum string makes with the horizontal is 81.4 ° when the acceleration of the pendulum bob is at a maximum.
[3]
[2]