9.5 Doppler Effect

A racing car is travelling at 300 km h⁻¹ on a race track.

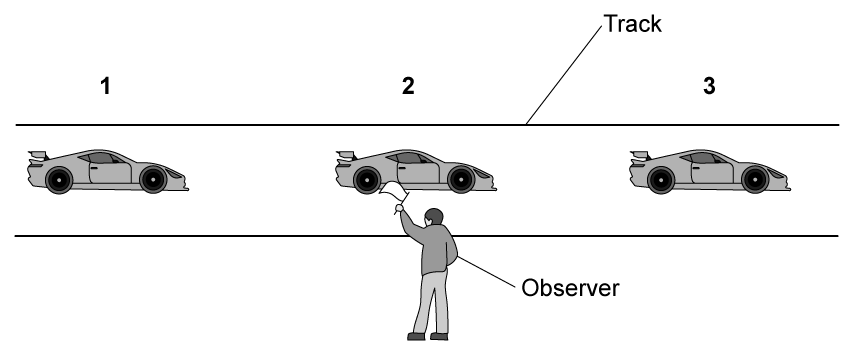
The stationary observer hears a frequency of sound of 1550 Hz from the exhaust as the car approaches them (position 1). You can assume the speed of sound to be 340 m s⁻¹.

The car from part (a) opens its Drag Reduction System (DRS) increasing its top speed by 10 km h⁻¹. It then overtakes another car which is travelling at 300 km h⁻¹.

The equation which can be used when both source and observer are moving is:

The frequency of the sound emitted by the car exhaust is directly proportional to the speed.

A scientist is doing some experiments on sound from the safety of the stands. An air horn emits a sound of frequency 450 Hz. The sound of the horn reflects off the car, which is moving away from the scientist, who measures the frequency as being 420 Hz.

A train is travelling at 45 m s⁻¹ and blows a whistle at a frequency of 750 Hz. A person is waiting at a level crossing for the train to pass. Take the speed of sound in air as 340 m s⁻¹.

After the train passes the level crossing, it slows down as it approaches a tunnel. Wind is funnelled down the tunnel towards the train reaching a velocity of 27 m s⁻¹. The observer at the level crossing hears the whistle at a frequency of 729 Hz. 

After exiting the tunnel, the train stops at a station. The observer from part (a) is now walking to the platform to catch the train at a speed of 1.5 m s⁻¹. The human ear can distinguish between frequency differences of around 3.6 Hz.

Once the train has left the station, it travels down a line with two tracks. Another train is approaching on the opposite track with a speed of 7.6 m s⁻¹. The speed of the departing train is 83% of the speed of the second train.

When both observer and source are moving, the following equation can be used to determine the new frequency:

Calculate the frequency of the whistle as observed by a passenger on the approaching train as a percentage of .

A ship is using low frequency sonar to map the sea bed. It sends out a pulse of sound which startles a nearby school of fish. The fish start to swim away at a speed of 20 km h⁻¹. The ship then sends out a second pulse with a wavelength that is 15 cm less than that of the original pulse. The fish perceive the two pulses to have the same frequency.

The school of fish approach a second ship which is emitting the same frequency of pulse as the first ship. They approach this boat at an angle of 38 °.

Calculate the frequency of sound as observed by the fish, .

The boat uses the stars to navigate. The captain uses a diffraction grating on her telescope to observe the light from a nearby asteroid she has spotted. She observes a spectral absorption line with a frequency of 673.7 nm. 

The absorption line for that element is given as 673.8 nm from tests in the laboratory. 

Two stars, A and B, in a binary system move in an anti-clockwise direction. Both stars emit light with wavelength, λ = 5.89 × 10⁻⁷ m, which reaches an observer on Earth. In the laboratory, the light is shown to fluctuate between wavelengths of 5.86 × 10⁻⁷ m and 6.02 × 10⁻⁷ m.

Assume they orbit in a circle around their common centre of mass.

The radius of orbit of star B is 4.98 × 10¹¹ m.