6.2 Newton’s Law of Gravitation

Question 1b

Marks: 4

Newton's Law of Gravitation can also be written in equation form:

$F = G \frac{M m}{r^{2}}$

(b)

Match the terms in the equation with the correct definition and unit:

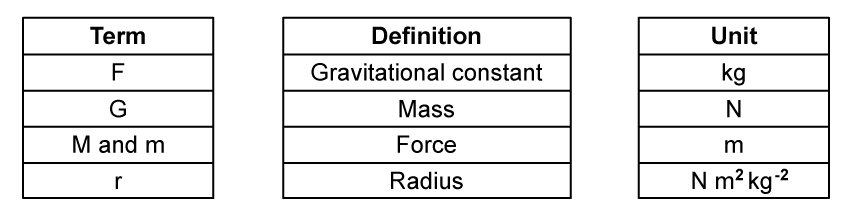
6-2-q1b-question-sl-sq-easy-phy

[4]

Key Concepts

Question 1c

Marks: 1

Newton's Law of Gravitation applies to point masses. Although planets are not point masses, the law also applies to planets orbiting the sun.

(c)

State why Newton's Law of Gravitation can apply to planets.

[1]

Key Concepts

Question 1d

Marks: 4

The mass of the Earth is 6.0 × 10²⁴ kg. A satellite of mass 5000 kg is orbiting at a height of 8500 km above the centre of the Earth.

(d)

Calculate the gravitational force between the Earth and the satellite.

[4]

Key Concepts

Question 2a

Marks: 4

The circular motion of a moon in orbit around a planet can be described by:

$v = \sqrt{\frac{G M}{r}}$

(a)

Define each of the terms in the equation above and give the unit:

(i)

v

[1]

(ii)

G

[1]

(iii)

M

[1]

(iv)

r

[1]

Key Concepts

Question 2b

Marks: 3

The moon Europa orbits the planet Jupiter at a distance of 670 900 km. The mass of Jupiter is 1.898 × 10²⁷ kg.

(b)

Calculate the linear velocity of Europa.

[3]

Key Concepts

Question 2c

Marks: 2

The mass of Europa is 4.8 × 10²² kg.

(c)

Calculate the gravitational force between Jupiter and Europa.

[2]

Key Concepts

Question 2d

Marks: 2

A second, hypothetical planet orbits Jupiter at a radius twice that of Europa, with the same mass. The gravitational force between two bodies is based on a $\frac{1}{r^{2}}$ rule.

(d)

Determine the force between Jupiter and the second planet as a fraction of the the force between Europa and Jupiter.

[2]

Key Concepts

Question 3a

Marks: 4

(a)

Complete the definition of Kepler's third law using words or phrases from the selection below:

For planets or satellites in a about the same central body, the of the time period is to the of the radius of the orbit.

circular orbit linear velocity square cube time

length mass proportional

[4]

Key Concepts

Question 3b

Marks: 4

Kepler's third law can also be represented by the equation:

$T^{2} = \frac{4 π^{2} r^{3}}{G M}$

(b)

Define each of the terms in the equation above and give the unit:

(i)

T

[1]

(ii)

G

[1]

(iii)

M

[1]

(iv)

r

[1]

Key Concepts

Question 3c

Marks: 3

Venus has an orbital period, T of 0.61 years and its orbital radius, r is 0.72 AU from the Sun.

(c)

Using these numbers, show that Kepler's Third Law,

T^{2} \propto r^{3}

is true for Venus. No unit conversions are necessary.

[3]

Key Concepts

Question 3d

Marks: 3

Kepler's Third Law $T^{2} \propto r^{3}$ can be represented graphically on log paper.

(d)

On the axes below, sketch a graph of

T^{2} \propto r^{3}

for our solar system, marking on the position of the Earth.

[3 marks]

Key Concepts

Circular Orbits
Newton’s Law of Gravitation

Question 4a

Marks: 4

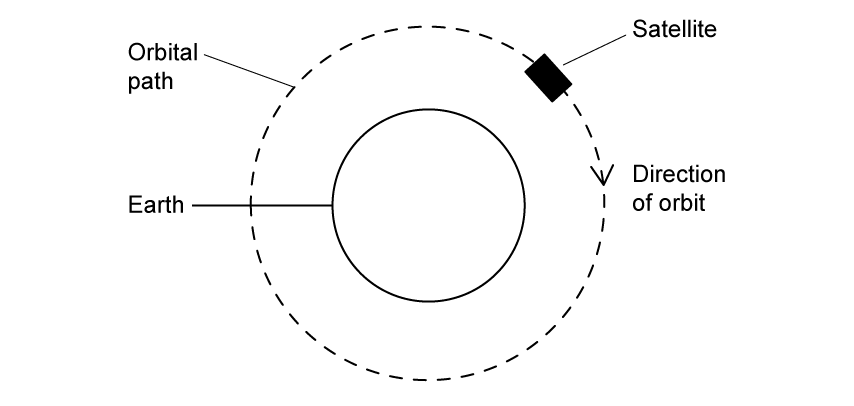
A satellite orbits the Earth in a clockwise direction.

6-2-q4a-question-sl-sq-easy-phy

(a)

Show on the diagram:

(i)

The centripetal force acting on the satellite when it is in orbit, F.

[2]

(ii)

The linear velocity of the satellite when it is in orbit, v.

[2]

Key Concepts

Question 4b

Marks: 1

(b)

State the name of the force which provides the centripetal force required to keep the satellite orbiting in a circular path.

[1]

Key Concepts

Newton’s Law of Gravitation
Circular Orbits

Question 4c

Marks: 3

The satellite has a mass of 7000 kg is in geostationary orbit and is constantly fixed above the same point on the Earth's surface. The radius of the geostationary orbit is 42 000 km. The Earth has a mass of 6.0 × 10²⁴ kg.

(c)

Calculate the force required to keep the satellite in this orbit.

[3]

Key Concepts

Question 4d

Marks: 2

All satellites in geostationary orbit are found at the same distance from the centre of the Earth, and are travelling at the same speed.

The equation linking speed of a satellite v and it's orbital radius, r is:

$v^{2} = \frac{G M}{r}$

where G is the gravitational constant and M is the mass of the Earth.

(d)

Discuss why the speed is the same for every satellite in geostationary orbit, including the relevance of the satellite's mass.

[2]

Key Concepts

Question 5a

Marks: 4

(a)

Define the following terms:

(i)

Gravitational field

[2]

(ii)

Gravitational field strength

[2]

Key Concepts

Question 5b

Marks: 3

Gravitational field strength can be written in equation form as:

$g = \frac{F}{m}$

(b)

Define each of the terms in the equation above and give the unit:

(i)

g

[1]

(ii)

F

[1]

(iii)

m

[1]

Key Concepts

Question 5c

Marks: 3

An astronaut of mass 80 kg stands on the Moon which has a gravitational field strength of 1.6 N kg⁻¹.

(c)

Calculate the weight of the astronaut on the Moon.

[3]

Key Concepts

Question 5d

Marks: 3

The mass of the Earth is 5.972 × 10²⁴ kg and sea level on the surface of the Earth is 6371 km.

(d)

Show that the gravitational field strength, g, is about 9.86 N kg⁻¹ at sea level.

[3]

Key Concepts