Question 1a

Marks: 3

A pendulum undergoes small-angle oscillations.

(a)

Outline the equation that defines simple harmonic motion.

Key Concepts

Conditions for SHM

Question 1b

Marks: 2

(b)

Sketch a graph to represent the change in amplitude,

x_{0}

against time for one swing of the pendulum. Start the time at zero seconds.

Key Concepts

Conditions for SHM

Question 1c

Marks: 2

The time period of 10 oscillations is found to be 12.0 s.

(c)

Determine the frequency when the bob is 1.0 cm from its equilibrium position.

Key Concepts

SHM Graphs

Question 1d

Marks: 4

The student wants to double the frequency of the pendulum swing. The time period, T of a simple pendulum is given by the equation:

T = 2π $\sqrt{\frac{L}{g}}$

where L is the length of the string and g is the acceleration due to gravity

(d)

Deduce the change which would achieve this.

Key Concepts

Describing Oscillations

Question 2a

Marks: 6

(a)

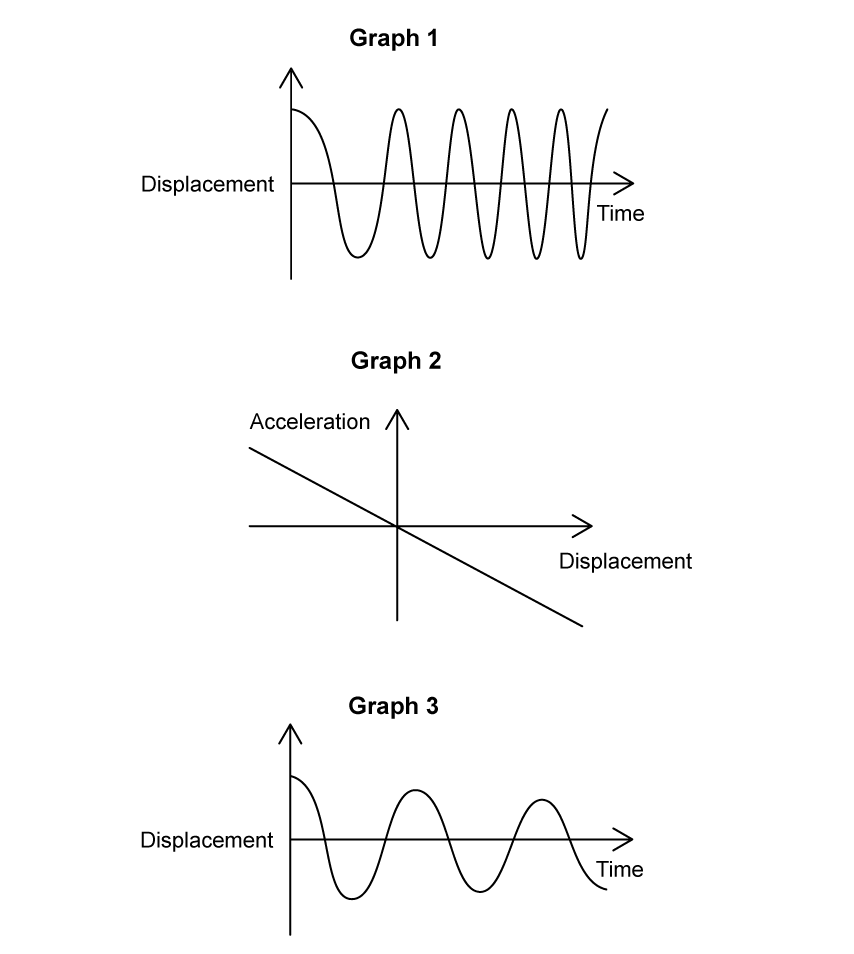
State and explain whether the motion of the objects in graphs I, II and III are simple harmonic oscillations

[6]

Question 2b

Marks: 2

(b)

Explain why, in practice, a freely oscillating pendulum cannot maintain a constant amplitude.

[2]

Question 2c

Marks: 3

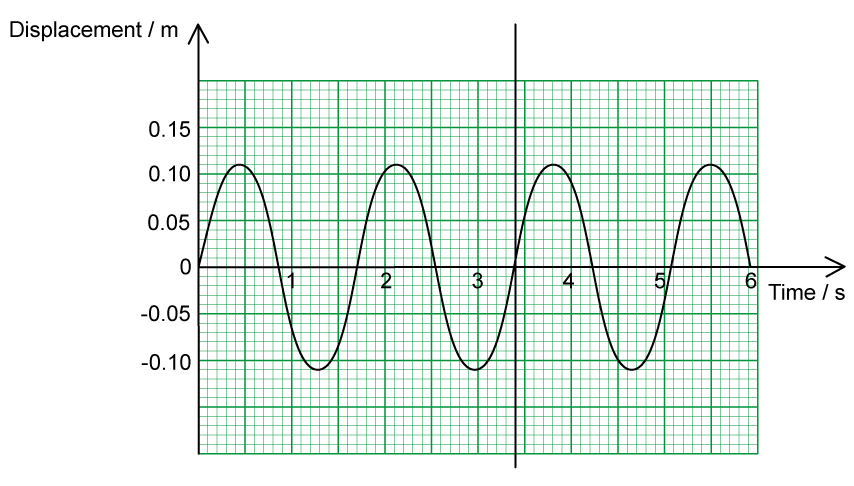
The motion of an object undergoing SHM is shown in the graph below.

sl-sq-4-1-hard-q5c-q-stem-graph

(c)

For this oscillator, determine:

(i)

The amplitude, A.

[1]

(ii)

The period, T.

[1]

(iii)

The frequency, f.

[1]

Question 2d

Marks: 3

(d)

Using the graph from part (c), state a time in seconds when the object performing SHM has:

(i)

Maximum positive velocity.

[1]

(ii)

Maximum negative acceleration.

[1]

(iii)

Maximum potential energy.

[1]

Question 3a

Marks: 3

A ball of mass 44 g on a 25 cm string oscillating in simple harmonic motion obeys the following equation:

a = −ω²x

(a)

Demonstrate mathematically that the graph of this equation is a downward sloping straight line that goes through the origin.

[3]

Question 3b

Marks: 3

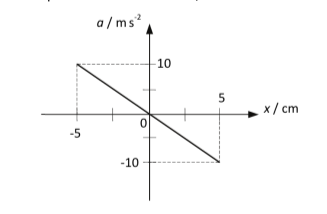
The graph below shows the acceleration, a, as a function of displacement, x, of the ball on the string.

4-1-hsq-6b-q-stem-graph

The angular speed, ω, in rad s⁻¹, is related to the frequency, f, of the oscillation by the following equation:

$ω = 2 π f$

(b)

For the ball on the string, determine the period, T, of the oscillation.

[3]

Question 3c

Marks: 4

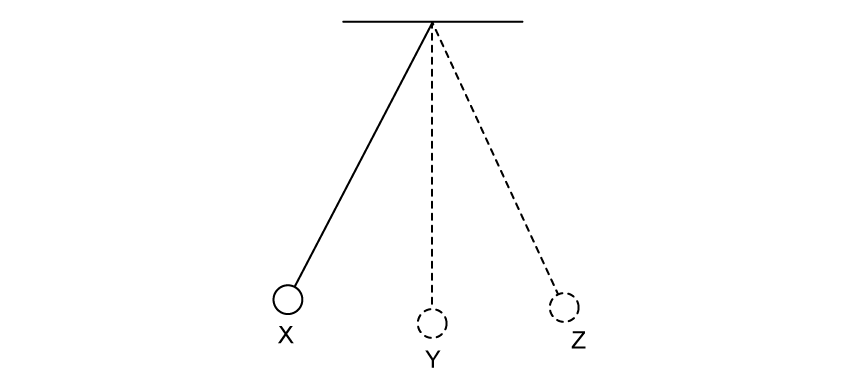
The ball is held in position X and then let go. The ball oscillates in simple harmonic motion.

(c)

Explain the change in acceleration as the ball on the string moves through half an oscillation from position X.

You can assume the ball is moving at position X.

[4]

Question 3d

Marks: 3

(d)

Describe the energy transfers occurring as the ball on the string completes half an oscillation from position X.

[3]

9-1-hl-mcq-medium-m10-question-stem

Question 4a

Marks: 3

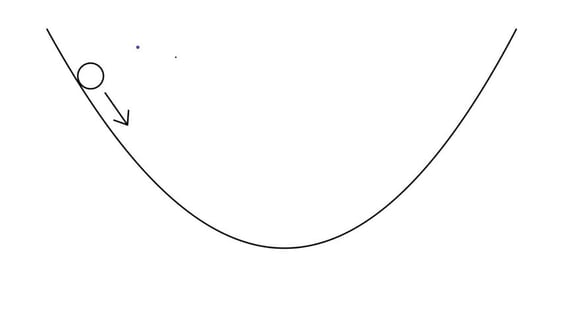
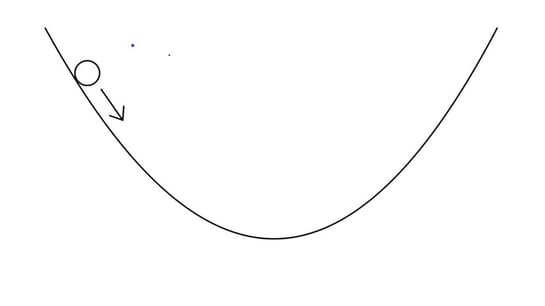
A smooth glass marble is held at the edge of a bowl and released. The marble rolls up and down the sides of the bowl with simple harmonic motion.

The magnitude of the restoring force which returns the marble to equilibrium is given by:

$F$ $= \frac{m g x}{R}$

Where $x$ is the displacement at a given time, and is the radius of the bowl. A~m~KSrC_q4a_oscillations_sl-ib-physics-sq-medium

(a)

Outline why the oscillations can be described as simple harmonic motion.

Key Concepts

Simple Harmonic Oscillations

Question 4b

Marks: 3

(b)

Describe the energy changes during the simple harmonic motion of the marble.

Key Concepts

Energy in SHM

Question 4c

Marks: 2

As the marble is released it has potential energy of 15 μJ. The mass of the marble is 3 g.

(c)

Calculate the velocity of the marble at the equilibrium position.

Key Concepts

SHM Graphs

Question 4d

Marks: 3

(d)

Sketch a graph to represent the kinetic, potential and total energy of the motion of the marble, assuming no energy is dissipated as heat. Clearly label any important values on the graph. A~m~KSrC_q4a_oscillations_sl-ib-physics-sq-medium

A~m~KSrC_q4a_oscillations_sl-ib-physics-sq-medium

Key Concepts

Energy in SHM

Question 5a

Marks: 3

An object is attached to a light spring and set on a frictionless surface. It is allowed to oscillate horizontally. Position 2 shows the equilibrium point. q5ab_oscillations_ib-sl-physics-sq-medium

a)

(i) Sketch a graph of acceleration against displacement for this motion.

[2]

(ii) On your graph, mark positions 1, 2 and 3 according to the diagram.

[1]

Key Concepts

SHM Graphs

Question 5b

Marks: 4

The mass begins its motion from position 1 and completes a full oscillation. q5ab_oscillations_ib-sl-physics-sq-medium

(b)

(i) Sketch a graph of velocity against time to show this.

[2]

(ii) On your graph, add labels to show points 1, 2 and 3

[2]

Key Concepts

SHM Graphs

Question 5c

Marks: 3

At the point marked Y on the graph, the potential energy of the block is E_P. The block has mass m, and the maximum velocity it achieves is v_max. q5c_oscillations_ib-sl-physics-sq-medium

(c)

Determine an equation for the potential energy at the point marked X.

Give your answer in terms of v_max , $v_{x}$ and m.

Key Concepts

Energy in SHM

Question 5d

Marks: 2

The graph shows how the displacement x of the mass varies with time t.

(d)

Determine the frequency of the oscillations.

Key Concepts

Describing Oscillations

DP IB Physics: HL

Topic Questions

4.1 Oscillations

Question 1a

Key Concepts

Question 1b

Key Concepts

Question 1c

Key Concepts

Question 1d

Key Concepts

Question 2a

Question 2b

Question 2c

Question 2d

Question 3a

Question 3b

Question 3c

Question 3d

Question 4a

Key Concepts

Question 4b

Key Concepts

Question 4c

Key Concepts

Question 4d

Key Concepts

Question 5a

Key Concepts

Question 5b

Key Concepts

Question 5c

Key Concepts

Question 5d

Key Concepts

Resources

Members

Company

Quick Links