DP Mathematics: Analysis and Approaches Questionbank

Topic 1—Number and algebra
Description
[N/A]Directly related questions
-
20N.1.AHL.TZ0.H_5:
The first term in an arithmetic sequence is and the fifth term is .
Find the common difference of the sequence, expressing your answer in the form , where .
-
20N.2.AHL.TZ0.H_6:
Use mathematical induction to prove that for .
-
20N.2.AHL.TZ0.H_7a:
There are more males than females in the group.
-
20N.1.SL.TZ0.T_15b:
Find the volume of the smallest slice of pie.
-
20N.1.SL.TZ0.T_15c:
The apple pie has a volume of .
Find the total number of slices Mia can cut from this pie.
-
20N.2.SL.TZ0.T_5d:
Find the amount of fuel pumped into the tank in the hour.
-
EXN.1.SL.TZ0.2:
Solve the equation . Give your answer in the form where .
-
EXN.3.AHL.TZ0.2c:
On an Argand diagram, plot and label all Gaussian integers that have a norm less than .
-
EXN.2.AHL.TZ0.7c:
Give a reason why the series expansion found in part (b) is not valid for .
-
21M.1.AHL.TZ1.9b:
Each pen may only contain one sheep. Amber and Brownie must not be placed in pens which share a boundary.
-
21M.2.SL.TZ1.7a.i:
Find the value of Amelia’s investment after years to the nearest hundred dollars.
-
21M.2.AHL.TZ1.8b:
Find the argument of in terms of .
-
21M.2.AHL.TZ1.8a:
Find the modulus of .
-
21M.2.SL.TZ2.3b:
Let denote the sum of the first terms of the sequence.
Find the maximum value of .
-
21M.3.AHL.TZ2.2f.i:
Write down expressions for and in terms of .
-
21N.1.AHL.TZ0.9a:
Find the value of and the value of .
-
21N.1.AHL.TZ0.11b:
Hence or otherwise, determine the Maclaurin series of in ascending powers of , up to and including the term in .
-
21N.1.AHL.TZ0.12b:
Plot the points , and on an Argand diagram.
-
21N.2.SL.TZ0.6b:
Find .
-
21N.2.AHL.TZ0.6b:
The equation has two real roots, and .
Consider the equation , where and which has roots and .
Without solving , determine the values of and . -
21N.2.AHL.TZ0.10a.ii:
-axis.
-
21N.2.AHL.TZ0.10e.ii:
Hence find the exact value of , expressing your answer as a single logarithm.
-
22M.3.AHL.TZ2.2f.ii:
Hence state a condition in terms of and that would imply has at least one complex root.
-
22M.3.AHL.TZ2.2h.iii:
By writing as a product of one linear and one cubic factor, prove that the equation has at least one complex root.
-
22M.1.SL.TZ1.2a:
The expression can be written as . Write down the value of .
-
22M.1.SL.TZ1.8b.ii:
Write down in the form , where .
-
22M.1.SL.TZ2.2a:
State the value of the first term, .
-
22M.1.SL.TZ2.2b:
Given that the th term of this sequence is , find the value of .
-
22M.1.AHL.TZ2.12b:
Given that , show that is a right-angled triangle.
-
22M.2.SL.TZ1.1b:
Find the value of required so that the amount in David’s account after years will be equal to the amount in Sam’s account.
-
22M.2.SL.TZ1.1c:
Find the interest David will earn over the years.
-
22M.2.AHL.TZ2.9a:
the digits are distinct.
-
22M.1.AHL.TZ1.1:
Find the value of .
-
22M.2.AHL.TZ1.12c.i:
By solving the differential equation, show that .
-
SPM.1.SL.TZ0.3b:
Hence, or otherwise, prove that the sum of the squares of any two consecutive odd integers is even.
-
EXM.1.AHL.TZ0.2c:
Use parts (a) and (b) to show that .
-
EXM.1.AHL.TZ0.2b:
Express the function in partial fractions.
-
EXM.3.AHL.TZ0.1j:
Write down the power series for .
-
EXM.3.AHL.TZ0.1g:
By differentiating both sides of the expression and then substituting , find the value of .
-
18M.1.SL.TZ1.T_7a.i:
For that day find how much weight was added after each lift.
-
18M.2.SL.TZ2.T_4b:
Calculate the café’s total profit for the first 12 weeks.
-
17M.1.SL.TZ1.T_5a:
Find the distance from the base of this ladder to the top rung.
-
16N.1.SL.TZ0.T_10a:
Find the value of the common ratio for this sequence.
-
17M.1.SL.TZ1.T_10c:
Find the sum of the first 30 terms of the sequence.
-
17M.1.SL.TZ2.S_1b:
Find the tenth term.
-
17M.1.AHL.TZ1.H_4:
Three girls and four boys are seated randomly on a straight bench. Find the probability that the girls sit together and the boys sit together.
-
18M.2.AHL.TZ2.H_5a:
Express the binomial coefficient as a polynomial in .
-
19M.2.AHL.TZ1.H_8b:
Use mathematical induction to prove that for , .
-
18N.2.AHL.TZ0.H_1a:
Find the common ratio of this sequence.
-
17N.1.AHL.TZ0.H_8:
Determine the roots of the equation , , giving the answers in the form where .
-
18N.1.SL.TZ0.T_1b:
Write down your answer to part (a) correct to the nearest integer.
-
18M.1.AHL.TZ1.H_6:
Use the principle of mathematical induction to prove that
, where .
-
17N.1.SL.TZ0.S_2a:
Find the common difference.
-
17M.1.AHL.TZ2.H_8:
Prove by mathematical induction that , where .
-
17M.1.SL.TZ1.T_2a:
Calculate the percentage of the population of Ottawa that speak English but not French.
-
19N.1.AHL.TZ0.H_10d:
The area enclosed by the graph of and the line can be expressed as . Find the value of .
-
19N.1.AHL.TZ0.H_3:
Three planes have equations:
, where .
Find the set of values of and such that the three planes have no points of intersection.
-
19N.2.AHL.TZ0.H_10a:
Find, in terms of , the probability that lies between 1 and 3.
-
19N.2.AHL.TZ0.H_8c:
the girls do not sit on either end and do not sit together.
-
19N.1.SL.TZ0.S_4b:
Hence or otherwise find the coefficient of the term in in the expansion of .
-
EXM.3.AHL.TZ0.2d:
Represent these solutions on an Argand diagram. Let their positions be denoted by placed in order in an anticlockwise direction round the circle, starting on the positive -axis. Show the positions of and .
-
18M.1.AHL.TZ1.H_11b:
Show that the area of the quadrilateral Q is .
-
20N.2.AHL.TZ0.H_11b:
Find an expression for in terms of .
-
20N.2.AHL.TZ0.H_11d:
Find the total distance travelled by in the first seconds of its motion.
-
20N.2.AHL.TZ0.H_3b:
Hence find the area of the shaded region.
-
20N.2.AHL.TZ0.H_4:
Find the term independent of in the expansion of .
-
20N.2.SL.TZ0.S_6b:
Find the values of for which the sum to infinity of the series exists.
-
20N.2.SL.TZ0.S_6c:
Find the value of when .
-
20N.2.SL.TZ0.T_5c:
Write down the common difference, .
-
EXN.1.AHL.TZ0.12a:
Use the binomial theorem to expand . Give your answer in the form where and are expressed in terms of and .
-
EXN.3.AHL.TZ0.2i:
Hence show that is a Gaussian prime.
-
EXN.3.AHL.TZ0.2d:
Given that where , show that .
-
EXN.3.AHL.TZ0.2e:
By expressing the positive integer as a product of two Gaussian integers each of norm , show that is not a Gaussian prime.
-
EXN.3.AHL.TZ0.2g:
Write down another prime number of the form that is not a Gaussian prime and express it as a product of two Gaussian integers.
-
EXN.2.AHL.TZ0.7a:
Find the value of and the value of .
-
21M.2.SL.TZ1.6:
Consider the expansion of , where .
Given that the coefficient of is , find the value of .
-
21M.3.AHL.TZ2.2e:
Suggest a value for .
-
21N.3.AHL.TZ0.1c.i:
.
-
21N.3.AHL.TZ0.1c.ii:
.
-
21N.2.AHL.TZ0.10c:
The oblique asymptote of the graph of can be written as where .
Find the value of and the value of .
-
21N.2.AHL.TZ0.10d:
Sketch the graph of for , clearly indicating the points of intersection with each axis and any asymptotes.
-
21N.3.AHL.TZ0.2a.i:
By solving the differential equation , show that where is a constant.
-
21N.3.AHL.TZ0.2b.iv:
Hence show that , where is a constant.
-
21N.3.AHL.TZ0.2c.ii:
Find the two values for that satisfy .
-
21N.3.AHL.TZ0.2a.iii:
Solve the differential equation in part (a)(ii) to find as a function of .
-
22M.3.AHL.TZ2.2b.i:
Show that .
-
22M.3.AHL.TZ2.2c:
Given that , deduce that and cannot all be real.
-
22M.3.AHL.TZ2.2g:
Use your result from part (f)(ii) to show that the equation has at least one complex root.
-
22M.1.SL.TZ1.9a.i:
Expand and simplify in ascending powers of .
-
22M.1.AHL.TZ1.10b.i:
Show that .
-
22M.1.AHL.TZ1.10b.ii:
Write down in the form , where .
-
22M.1.SL.TZ2.3a:
Prove that the sum of these three integers is always divisible by .
-
22M.1.SL.TZ2.3b:
Prove that the sum of the squares of these three integers is never divisible by .
-
22M.2.AHL.TZ1.9a:
Find the number of ways these five people can be seated in this row.
-
22M.2.AHL.TZ2.9b:
the digits are distinct and are in increasing order.
-
22M.1.SL.TZ2.8b:
Find the value of and the value of .
-
SPM.2.SL.TZ0.3a:
Find the value of r, giving your answer to four significant figures.
-
SPM.1.SL.TZ0.3a:
Show that , where .
-
EXM.2.AHL.TZ0.1b:
By substituting find a rational approximation to .
-
EXM.3.AHL.TZ0.4c.ii:
the number of years it will take for the population to triple.
-
17N.1.SL.TZ0.T_9a:
Calculate the original price of the bicycle.
-
17N.2.SL.TZ0.T_2b:
Find the value of .
-
16N.1.SL.TZ0.T_10b:
Find the distance that the post is driven into the ground by the eighth strike of the hammer.
-
16N.1.SL.TZ0.T_10c:
Find the total depth that the post has been driven into the ground after 10 strikes of the hammer.
-
17M.1.AHL.TZ1.H_8:
Use the method of mathematical induction to prove that is divisible by 9 for .
-
17M.1.SL.TZ2.T_9a:
Write down the common ratio of the sequence.
-
16N.1.SL.TZ0.T_13a:
Find the year in which the comet was seen from Earth for the fifth time.
-
17N.1.AHL.TZ0.H_10b.i:
Determine the mean of X.
-
18M.2.AHL.TZ2.H_5b:
Hence find the least value of for which .
-
17N.1.AHL.TZ0.H_11d:
Show that, for , the equation of the tangent to the curve at is .
-
19M.2.SL.TZ1.T_5e:
John purchased the bicycle in 2008.
Justify why John should not insure his bicycle in 2019.
-
18M.2.SL.TZ2.T_4d:
Calculate the tea-shop’s total profit for the first 12 weeks.
-
17M.1.AHL.TZ2.H_11a:
Solve .
-
18M.2.SL.TZ1.S_8b:
Use the regression equation to estimate the value of y when x = 3.57.
-
16N.1.AHL.TZ0.H_12a:
Determine the value of
(i) ;
(ii) .
-
18M.2.AHL.TZ2.H_1b:
Find the exact value of the modulus of .
-
17N.2.AHL.TZ0.H_1:
Boxes of mixed fruit are on sale at a local supermarket.
Box A contains 2 bananas, 3 kiwifruit and 4 melons, and costs $6.58.
Box B contains 5 bananas, 2 kiwifruit and 8 melons and costs $12.32.
Box C contains 5 bananas and 4 kiwifruit and costs $3.00.
Find the cost of each type of fruit.
-
19M.1.SL.TZ2.T_1c:
Write your answer to part (b) in the form , where 1 ≤ < 10 , .
-
18N.1.SL.TZ0.T_1c:
Write down your answer to part (b) in the form a × 10k , where 1 ≤ a < 10 and k ∈ .
-
17M.2.AHL.TZ2.H_6:
Given that , find in terms of .
-
19M.2.AHL.TZ1.H_6a:
Show the points represented by and on the following Argand diagram.
-
19M.1.AHL.TZ1.H_11a.ii:
Find how many sets of three points can be selected which can form the vertices of a triangle.
-
19M.1.AHL.TZ1.H_11c:
Write down the value of corresponding to the point .
-
19M.1.AHL.TZ1.H_11e:
Let be the point on with coordinates (1, 0, 1) and be the point on with parameter .
Find the area of the quadrilateral .
-
17N.1.SL.TZ0.T_3a:
Calculate the time, in minutes, it takes for light from the Sun to reach the Earth.
-
17M.1.SL.TZ1.T_2b:
Calculate the number of people in Ottawa that speak both English and French.
-
19N.3.AHL.TZ0.Hdm_2a.ii:
Find the remainder when is divided by .
-
19N.3.AHL.TZ0.Hdm_2b:
Convert to base , where .
-
19N.3.AHL.TZ0.Hdm_2c:
Consider the equation .
Find the value of .
-
19N.1.SL.TZ0.S_10a:
Write down the coordinates of .
-
19M.1.AHL.TZ1.H_11a.i:
Find how many sets of four points can be selected which can form the vertices of a quadrilateral.
-
EXM.3.AHL.TZ0.2e:
Show that the length of the line segment is .
-
SPM.1.AHL.TZ0.11b:
Find , and expressing your answers in the form , where and .
-
EXM.3.AHL.TZ0.2b:
Hence show that .
-
18M.1.SL.TZ1.S_10a.i:
Find an expression for r in terms of θ.
-
20N.2.SL.TZ0.S_6a:
Find the common ratio in terms of .
-
20N.2.SL.TZ0.T_5f:
Find the total amount of fuel pumped into the tank in the first hours.
-
EXN.2.AHL.TZ0.8:
Prove by contradiction that is an irrational number.
-
EXN.2.SL.TZ0.7a:
Show that .
-
EXN.2.AHL.TZ0.7b:
Hence, expand in ascending powers of , up to and including the term in .
-
21M.1.AHL.TZ1.7:
Consider the quartic equation .
Two of the roots of this equation are and , where .
Find the possible values of .
-
21M.2.AHL.TZ1.8c.i:
Find the minimum value of .
-
21M.2.AHL.TZ2.7a:
in the position immediately after Andrea.
-
21M.2.AHL.TZ2.7b:
in any position after Andrea.
-
21M.3.AHL.TZ2.2c:
By factorizing , or otherwise, deduce that .
-
21N.1.SL.TZ0.8a:
Show that .
-
21N.1.AHL.TZ0.11a:
Prove by mathematical induction that for .
-
21N.2.SL.TZ0.6a:
Find the first term of the sequence, .
-
21N.3.AHL.TZ0.2b.iii:
Hence find as a function of .
-
22M.3.AHL.TZ1.1f:
A polygonal number, , can be represented by the series
where .
Use mathematical induction to prove that where .
-
22M.3.AHL.TZ1.2e:
Deduce from part (d)(i) that the complex roots of the equation can be expressed as .
-
22M.3.AHL.TZ1.2f.i:
Use this diagram to determine the roots of the corresponding equation of the form for .
-
22M.1.SL.TZ1.8a.i:
Show that .
-
22M.1.SL.TZ2.6b:
The third term in the expansion is the mean of the second term and the fourth term in the expansion.
Find the possible values of .
-
22M.1.AHL.TZ2.12e:
Consider the equation , where and .
Given that , deduce that only one equilateral triangle can be formed from the point and the roots of this equation.
-
22M.1.AHL.TZ2.12d:
Use the result from part (c)(ii) to show that .
-
22M.1.AHL.TZ2.12c.i:
Express in terms of .
-
22M.2.SL.TZ1.1a:
Find the amount that Sam will have in his account after years.
-
SPM.2.AHL.TZ0.8:
The complex numbers and satisfy the equations
.
Find and in the form where , .
-
EXM.1.AHL.TZ0.3b:
Use part (a) to show that is always decreasing.
-
EXM.2.AHL.TZ0.1a:
Write down and simplify the first three terms, in ascending powers of , in the Extended Binomial expansion of .
-
EXM.3.AHL.TZ0.4b.ii:
the number of years it will take for the population to triple.
-
EXM.3.AHL.TZ0.4a:
Show that the general solution of this differential equation is , where .
-
EXM.3.AHL.TZ0.4b.iii:
-
19M.2.SL.TZ1.S_7a:
Write down the first three non-zero terms of .
-
19M.2.SL.TZ2.T_6a:
Determine the amount that he will have in his account after 3 years. Give your answer correct to two decimal places.
-
17N.1.SL.TZ0.T_9b:
Calculate the difference between the original price of the bicycle and the total amount Juan will pay.
-
17N.2.SL.TZ0.T_2c:
Calculate the total distance, in kilometres, Rosa runs in the first 50 training sessions.
-
17M.1.SL.TZ1.T_5b:
The company also makes a ladder that is 1050 cm long.
Find the maximum number of rungs in this 1050 cm long ladder.
-
17M.2.SL.TZ1.S_6:
Let . Find the term in in the expansion of the derivative, .
-
18N.1.AHL.TZ0.H_2a:
Find the number of different possible teams that could be chosen.
-
17M.1.AHL.TZ1.H_1:
Find the solution of .
-
18M.2.AHL.TZ1.H_7a:
Show that there will be approximately 2645 fish in the lake at the start of 2020.
-
19M.2.AHL.TZ1.H_2b:
where , .
-
17M.1.AHL.TZ1.H_2a.i:
By expressing and in modulus-argument form write down the modulus of ;
-
17M.1.AHL.TZ1.H_2a.ii:
By expressing and in modulus-argument form write down the argument of .
-
18N.1.AHL.TZ0.H_4a:
Find the value of for which the system of equations does not have a unique solution.
-
17N.1.SL.TZ0.S_2b:
Find the tenth term.
-
18M.1.SL.TZ2.T_3b.ii:
Find the value of x.
-
16N.1.SL.TZ0.T_1b:
Write your answer to part (a)
(i) correct to two decimal places;
(ii) correct to three significant figures.
-
19N.1.SL.TZ0.S_10b:
Given that , find the equation of in terms of , and .
-
19M.2.AHL.TZ1.H_11c:
Given that , find the other two real roots.
-
18M.2.SL.TZ2.S_4b:
Find the sum of the first 8 terms.
-
18N.1.AHL.TZ0.H_11b.iii:
Hence, or otherwise, show that S = .
-
18N.1.AHL.TZ0.H_11b.ii:
By writing as , find the value of cos in the form , where , and are integers to be determined.
-
17N.2.AHL.TZ0.H_12d.ii:
Hence or otherwise, find the minimum value of that would permit David to withdraw annual amounts of $5000 indefinitely. Give your answer to the nearest dollar.
-
18M.1.AHL.TZ1.H_11a.ii:
Sketch on an Argand diagram the points represented by w0 , w1 , w2 and w3.
-
18M.1.SL.TZ2.T_5b:
Karl decides to donate this interest to a charity in France. The charity receives 170 euros (EUR). The exchange rate is 1 USD = t EUR.
Calculate the value of t.
-
18M.1.SL.TZ2.T_5a.i:
Calculate the amount of money he has in the account after 5 years.
-
18N.1.AHL.TZ0.H_8:
Consider the equation , where , , , and .
Two of the roots of the equation are log26 and and the sum of all the roots is 3 + log23.
Show that 6 + + 12 = 0.
-
20N.1.AHL.TZ0.H_12b:
State the equation of the horizontal asymptote on the graph of .
-
20N.1.AHL.TZ0.H_12e:
The region bounded by the -axis, the curve , and the lines and is rotated through about the -axis. Find the volume of the solid generated, giving your answer in the form , where .
-
20N.2.AHL.TZ0.H_11c:
Find the maximum displacement of , in metres, from its initial position.
-
20N.1.SL.TZ0.T_1b:
Calculate James’s estimate of its volume, in .
-
20N.1.SL.TZ0.T_1c:
The actual volume of the asteroid is found to be .
Find the percentage error in James’s estimate of the volume.
-
20N.1.SL.TZ0.T_8b:
At the end of the years, Imon withdrew from the fixed deposit account and reinvested this into a super-savings account with a nominal annual interest rate of , compounded half-yearly.
The value of the super-savings account increased to after months.
Find the value of .
-
20N.2.SL.TZ0.T_5b:
Show that the volume of the tank is , correct to three significant figures.
-
EXN.1.AHL.TZ0.12b:
Use de Moivre’s theorem and the result from part (a) to show that .
-
EXN.2.AHL.TZ0.9:
A biased coin is weighted such that the probability, , of obtaining a tail is . The coin is tossed repeatedly and independently until a tail is obtained.
Let be the event “obtaining the first tail on an even numbered toss”.
Find .
-
EXN.3.AHL.TZ0.2a:
Find .
-
21M.1.SL.TZ1.2a:
Write down the radius of the planet.
-
21M.1.SL.TZ1.3:
Consider an arithmetic sequence where . Find the value of the first term, , and the value of the common difference, .
-
21M.2.SL.TZ1.7a.ii:
Determine the number of years required for Amelia’s investment to reach the target.
-
21M.2.SL.TZ1.7b:
Bill invests his in an account that offers an interest rate of per annum compounded monthly, where is set to two decimal places.
Find the minimum value of needed for Bill to reach the target after years.
-
21M.2.AHL.TZ1.12b:
Hence, find an expression for .
-
21M.3.AHL.TZ2.2a.i:
Show that .
-
21N.1.SL.TZ0.6a:
Show that .
-
21N.1.SL.TZ0.8d.ii:
Find the value of and the value of .
-
21N.1.AHL.TZ0.11c:
Hence or otherwise, determine the value of .
-
21N.2.AHL.TZ0.10b:
Write down the equation of the vertical asymptote of the graph of .
-
21N.3.AHL.TZ0.1b:
Show that .
-
21N.3.AHL.TZ0.1a:
Verify that satisfies the differential equation .
-
21N.3.AHL.TZ0.2c.i:
Show that .
-
22M.3.AHL.TZ1.1b.iii:
For , sketch a diagram clearly showing your answer to part (b)(ii).
-
22M.3.AHL.TZ1.2a.i:
Given that and are roots of the equation, write down the third root.
-
22M.3.AHL.TZ1.2a.ii:
Verify that the mean of the two complex roots is .
-
22M.3.AHL.TZ2.2a:
By expanding show that:
.
-
22M.3.AHL.TZ2.2d:
Using the result from part (c), show that when , this equation has at least one complex root.
-
22M.1.SL.TZ2.6a:
Show that .
-
22M.1.AHL.TZ2.9:
Prove by contradiction that the equation has no integer roots.
-
22M.1.AHL.TZ1.11c:
Find the distance between and .
-
22M.1.SL.TZ1.9a.ii:
By using a suitable substitution for , show that .
-
22M.1.AHL.TZ1.11b.ii:
Find a vector equation of , the line of intersection of and .
-
22M.2.AHL.TZ1.12c.ii:
Find the actual value of when .
-
EXM.1.AHL.TZ0.2a:
Very briefly, explain why the value of this integral must be negative.
-
EXM.3.AHL.TZ0.1f:
By substituting , find the value of .
-
EXM.3.AHL.TZ0.1i:
Hence, write down the first four terms in what is called the Extended Binomial Theorem for .
-
EXM.3.AHL.TZ0.4b.i:
the population after 10 years
-
17M.1.SL.TZ1.T_10a:
Find the value of , the common ratio of the sequence.
-
17M.1.SL.TZ2.S_1a:
Find the common difference.
-
17M.1.SL.TZ1.T_10b:
Find the value of for which .
-
16N.1.AHL.TZ0.H_13c:
Use the principle of mathematical induction to prove that
where .
-
19M.1.AHL.TZ2.H_7:
Solve the simultaneous equations
.
-
17M.1.AHL.TZ1.H_7b:
determine the value of .
-
17N.1.AHL.TZ0.H_10a:
Show that the probability that Chloe wins the game is .
-
19M.2.AHL.TZ1.H_8a:
Solve the inequality .
-
18N.1.SL.TZ0.S_3a:
Find u8.
-
19M.2.SL.TZ1.T_5c:
Calculate, in years, when the bicycle value will be less than 50 USD.
-
19M.2.SL.TZ2.T_6b:
Find the difference between the cost of the bicycle and the amount of money in Tommaso’s account after 3 years. Give your answer correct to two decimal places.
-
18M.2.SL.TZ1.S_7b:
Hence find the value of n such that .
-
18N.1.AHL.TZ0.H_4b:
Find the solution of the system of equations when .
-
19M.1.SL.TZ2.T_1b:
Give your answer to part (a) correct to three significant figures.
-
19M.2.AHL.TZ1.H_6b.i:
Find an expression in terms of θ for .
-
16N.1.SL.TZ0.T_1c:
Write your answer to part (b)(ii) in the form , where .
-
19N.1.AHL.TZ0.H_5b:
The solutions form the vertices of a polygon in the complex plane. Find the area of the polygon.
-
19N.2.AHL.TZ0.H_11b:
Find the area of .
-
19N.1.AHL.TZ0.H_6:
Consider the function , where . The derivative of is denoted by .
Prove, by mathematical induction, that , .
-
19N.1.SL.TZ0.S_1a:
Find the common difference.
-
EXM.3.AHL.TZ0.2a:
By considering the area of two triangles and the area of the sector show that .
-
SPM.1.AHL.TZ0.11d:
By considering the sum of the roots , and , show that
.
-
17M.1.AHL.TZ2.H_5:
In the following Argand diagram the point A represents the complex number and the point B represents the complex number . The shape of ABCD is a square. Determine the complex numbers represented by the points C and D.
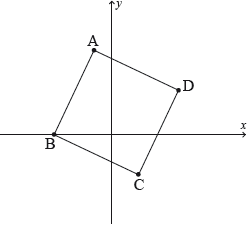
-
EXM.3.AHL.TZ0.2g:
Using part (b) find the limit of this perimeter as .
-
17N.1.SL.TZ0.S_10b:
The following diagram shows [CD], with length , where . Squares with side lengths , where , are drawn along [CD]. This process is carried on indefinitely. The diagram shows the first three squares.
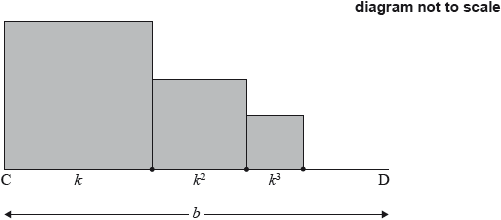
The total sum of the areas of all the squares is . Find the value of .
-
19M.2.AHL.TZ1.H_11a:
Show that .
-
20N.2.SL.TZ0.S_5:
Consider the expansion of , where .
The coefficient of the term in is . Find the value of .
-
20N.2.SL.TZ0.T_5a:
Find , the height of the tank.
-
EXN.3.AHL.TZ0.2b:
Determine whether is a Gaussian integer.
-
EXN.3.AHL.TZ0.2h:
Show that .
-
21M.2.AHL.TZ1.8c.ii:
For the value of found in part (i), find the value of .
-
21M.3.AHL.TZ2.2a.ii:
Hence, deduce that .
-
21M.2.AHL.TZ2.8:
Consider where .
Show that .
-
21M.2.AHL.TZ2.9a:
Write down the first three terms of the binomial expansion of in ascending powers of .
-
21N.1.SL.TZ0.6b:
Hence or otherwise, solve the equation for .
-
21N.1.AHL.TZ0.9b:
State the restriction which must be placed on for this expansion to be valid.
-
21N.2.SL.TZ0.6c:
Find the least value of such that .
-
21N.2.AHL.TZ0.10a.i:
-axis.
-
21N.3.AHL.TZ0.2a.ii:
Show that .
-
22M.3.AHL.TZ1.1a.i:
For triangular numbers, verify that .
-
22M.3.AHL.TZ1.2f.ii:
State the coordinates of .
-
22M.1.AHL.TZ1.8:
Consider integers and such that is exactly divisible by . Prove by contradiction that and cannot both be odd.
-
22M.1.AHL.TZ1.10a.i:
Show that .
-
SPM.1.SL.TZ0.6b:
Hence or otherwise solve for .
-
EXM.1.AHL.TZ0.1:
Let for . Use partial fractions to find .
-
EXM.3.AHL.TZ0.1c:
Differentiate the equation obtained part (b) and hence, find the first four terms in a power series for .
-
19M.2.SL.TZ1.T_5a:
Calculate, in CAD, the total amount John pays for the bicycle.
-
17M.1.AHL.TZ2.H_3a:
the value of ;
-
17M.1.SL.TZ2.T_5b:
Find the total number of sticks used by Tomás for all 24 diagrams.
-
18N.1.AHL.TZ0.H_2b:
Find the number of different possible teams that could be chosen, given that the team must include at least one girl and at least one boy.
-
17M.1.SL.TZ2.T_1c:
Write your answer to part (b)(ii) in the form , where .
-
17N.1.AHL.TZ0.H_11c:
Hence or otherwise, find an expression for the derivative of with respect to .
-
18M.1.SL.TZ1.T_7b:
On that day, Sergei made 12 successive lifts. Find the total combined weight of these lifts.
-
18M.2.AHL.TZ1.H_1b:
Calculate the number of positive terms in the sequence.
-
19M.2.SL.TZ1.S_7b.ii:
Find the value of .
-
18M.2.SL.TZ1.S_8a:
Find the value of a and of b.
-
19M.1.SL.TZ2.T_1a:
Use this model to calculate the circumference of the Moon in kilometres. Give your full calculator display.
-
16N.1.AHL.TZ0.H_12b:
Show that .
-
18M.2.AHL.TZ2.H_6:
Use mathematical induction to prove that for where .
-
19M.1.AHL.TZ1.H_11d:
Write down and .
-
19N.2.AHL.TZ0.H_10b:
Sketch the graph of . State the coordinates of the end points and any local maximum or minimum points, giving your answers in terms of .
-
19N.1.SL.TZ0.S_4a:
Find the value of .
-
18M.2.SL.TZ2.S_4c:
Find the least value of n for which Sn > 163.
-
18M.1.SL.TZ1.S_10c:
Find the values of θ which give the greatest value of the sum.
-
18N.1.AHL.TZ0.H_11a:
Find the roots of which satisfy the condition , expressing your answers in the form , where , .
-
SPM.1.AHL.TZ0.11a:
Express in the form , where and .
-
EXM.3.AHL.TZ0.2c:
Let . Working in modulus/argument form find the solutions to this equation.
-
EXM.3.AHL.TZ0.2f:
Hence, write down the total length of the perimeter of the regular sided polygon .
-
17N.2.AHL.TZ0.H_12b:
Show that the total value of Phil’s savings after 20 years is .
-
EXM.3.AHL.TZ0.2i:
Using part (b) find the limit of this area as .
-
18N.1.AHL.TZ0.H_11b.i:
Show that Re S = Im S.
-
18M.2.SL.TZ2.S_4a:
Find the common ratio.
-
17M.1.SL.TZ1.S_7a:
Find the common ratio.
-
19M.2.AHL.TZ1.H_11b:
Show that one of the real roots is equal to 1.
-
17N.2.AHL.TZ0.H_12d.i:
David wishes to withdraw $5000 at the end of each year for a period of years. Show that an expression for the minimum value of is
.
-
17M.2.SL.TZ2.S_5:
Consider a geometric sequence where the first term is 768 and the second term is 576.
Find the least value of such that the th term of the sequence is less than 7.
-
20N.1.AHL.TZ0.H_4:
Consider the equation , where and .
Find the value of and the value of .
-
20N.2.AHL.TZ0.H_11e.i:
Show that, at these times, .
-
20N.2.AHL.TZ0.H_11e.ii:
Hence show that .
-
20N.2.AHL.TZ0.H_3a:
Determine the values of , and .
-
20N.2.AHL.TZ0.H_7b:
Two of the teachers, Gary and Gerwyn, refuse to go out for a meal together.
-
20N.3.AHL.TZ0.Hdm_3a.i:
Write down the remainder when is divided by .
-
20N.3.AHL.TZ0.Hdm_3a.ii:
Use Fermat’s little theorem to find the remainder when is divided by .
-
20N.3.AHL.TZ0.Hdm_3b.i:
Prove that a number in base is divisible by if, and only if, the sum of its digits is divisible by .
-
20N.1.SL.TZ0.T_1a:
Write down the value of the iron in the form where .
-
20N.2.SL.TZ0.T_5e.ii:
Write down the number of hours that the pump was pumping fuel into the tank.
-
20N.2.SL.TZ0.T_5g:
Show that the tank will never be completely filled using this pump.
-
EXN.1.SL.TZ0.4b:
Prove that the sum of the first terms of this arithmetic sequence is a square number.
-
EXN.1.AHL.TZ0.9:
It is given that . (Do not prove this identity.)
Using mathematical induction and the above identity, prove that for .
-
EXN.1.AHL.TZ0.12c:
Use the identity from part (b) to show that the quadratic equation has roots and .
-
EXN.2.SL.TZ0.7c.ii:
For the value of found in part (c) (i), state Helen’s annual salary and Jane’s annual salary, correct to the nearest dollar.
-
EXN.2.SL.TZ0.7d:
Find Jane’s total earnings at the start of her th year of employment. Give your answer correct to the nearest dollar.
-
EXN.3.AHL.TZ0.2f:
Verify that is not a Gaussian prime.
-
21M.1.AHL.TZ1.9a:
Each pen is large enough to contain five sheep. Amber and Brownie must not be placed in the same pen.
-
21M.2.SL.TZ1.7c.ii:
Find the amount Chris needs to deposit initially in order to reach the target after years. Give your answer to the nearest dollar.
-
21M.1.SL.TZ2.4:
In the expansion of , where , the coefficient of the term in is .
Find the possible values of .
-
21M.3.AHL.TZ2.2f.ii:
Hence, write down an expression for in terms of and .
-
21M.3.AHL.TZ2.2b:
Show that .
-
21N.1.SL.TZ0.8c:
Find the value of .
-
21N.1.SL.TZ0.8d.i:
Show that and are four consecutive terms in a geometric sequence.
-
21N.1.AHL.TZ0.12c:
Find .
-
21N.1.AHL.TZ0.12d:
By using de Moivre’s theorem, show that is a root of this equation.
-
21N.1.AHL.TZ0.12a.i:
Verify that is a root of this equation.
-
21N.2.AHL.TZ0.10e.i:
Express in partial fractions.
-
21N.3.AHL.TZ0.2c.iii:
Let the two values found in part (c)(ii) be and .
Verify that is a solution to the differential equation in (c)(i),where is a constant.
-
21N.3.AHL.TZ0.2b.i:
By differentiating with respect to , show that .
-
22M.3.AHL.TZ1.1b.ii:
State, in words, what the identity given in part (b)(i) shows for two consecutive triangular numbers.
-
22M.3.AHL.TZ1.1d:
Hence show that for .
-
22M.3.AHL.TZ1.1e:
By using a suitable table of values or otherwise, determine the smallest positive integer, greater than , that is both a triangular number and a pentagonal number.
-
22M.3.AHL.TZ2.2h.i:
State what the result in part (f)(ii) tells us when considering this equation .
-
22M.1.AHL.TZ1.10b.iii:
The sum of the first terms of the series is .
Find the value of .
-
22M.1.AHL.TZ1.9a:
Find an expression for in terms of .
-
22M.1.AHL.TZ1.10a.ii:
Hence or otherwise, show that the series is convergent.
-
22M.1.AHL.TZ1.10a.iii:
Given that and , find the value of .
-
22M.1.AHL.TZ2.12a:
Show that where is the complex conjugate of .
-
22M.1.AHL.TZ2.12c.ii:
Hence show that .
-
SPM.2.SL.TZ0.3b:
Laurie makes no further deposits to or withdrawals from the account.
Find the year in which the amount of money in Laurie’s account will become double the amount she invested.
-
EXM.1.SL.TZ0.1b:
Hence prove that the square of any integer can be written in the form or , where .
-
EXM.3.AHL.TZ0.1k:
Hence, using integration, find the power series for , giving the first four non-zero terms.
-
EXM.3.AHL.TZ0.1b:
Consider the power series
By considering the ratio of consecutive terms, explain why this series is equal to and state the values of for which this equality is true.
-
EXM.3.AHL.TZ0.4e:
Solve the differential equation , giving your answer in the form .
-
19M.2.SL.TZ2.S_10b:
Find the exact value of .
-
17N.2.SL.TZ0.T_2e:
Calculate the total distance Carlos runs in the first year.
-
17M.1.SL.TZ2.S_1c:
Find the sum of the first ten terms of the sequence.
-
17M.1.AHL.TZ2.H_3b:
the value of ;
-
18N.1.AHL.TZ0.H_6:
Use mathematical induction to prove that , for .
-
16N.1.AHL.TZ0.H_13a:
Find the value of .
-
19M.1.SL.TZ1.S_10a:
Find the two smallest non-zero values of for which .
-
17M.1.SL.TZ2.T_1a:
Calculate . Give your full calculator display.
-
16N.1.AHL.TZ0.H_7:
Solve the equation .
-
17N.1.AHL.TZ0.H_11a:
Determine whether is an odd or even function, justifying your answer.
-
18M.1.SL.TZ1.T_7a.ii:
For that day find the weight of Sergei’s first lift.
-
19M.2.SL.TZ1.T_5d:
Find the total amount John has paid to insure his bicycle for the first 5 years.
-
18M.2.SL.TZ1.S_7a:
Given that xk + 1 = xk + a, find a.
-
17M.1.AHL.TZ2.H_11c.ii:
Hence find the cube roots of in modulus-argument form.
-
19M.2.AHL.TZ2.H_8b:
One of the roots satisfies the condition .
Given that , express in the form , where , .
-
18M.2.AHL.TZ2.H_1a:
Express in the form , where .
-
19M.2.AHL.TZ1.H_6b.ii:
Find an expression in terms of θ for .
-
19M.2.AHL.TZ1.H_6c:
Hence or otherwise find the value of θ for which .
-
18M.1.SL.TZ2.T_3a:
Find the length, in cm, of this line. Give your answer in the form a × 10k , where 1 ≤ a < 10 and k ∈ .
-
18M.1.SL.TZ2.T_3b.i:
Write down the length of the Amazon River in cm.
-
17N.1.SL.TZ0.T_3b:
Find the distance from the Earth to Polaris in millions of km. Give your answer in the form with and .
-
17M.2.AHL.TZ2.H_8:
In a trial examination session a candidate at a school has to take 18 examination papers including the physics paper, the chemistry paper and the biology paper. No two of these three papers may be taken consecutively. There is no restriction on the order in which the other examination papers may be taken.
Find the number of different orders in which these 18 examination papers may be taken.
-
16N.1.SL.TZ0.T_1a:
Calculate the value of . Write down your full calculator display.
-
19N.1.AHL.TZ0.H_10c:
Show that .
-
19N.2.AHL.TZ0.H_11c:
The region is now rotated about the -axis, through radians, to form a solid.
By writing as , show that the volume of the solid formed is .
-
19N.3.AHL.TZ0.Hdm_2a.i:
State Fermat’s little theorem.
-
19N.2.AHL.TZ0.H_1:
A geometric sequence has and . Find the second term of the sequence.
-
19N.2.AHL.TZ0.H_8a:
the girls do not sit together.
-
19N.1.SL.TZ0.S_1b:
Find the first term.
-
19N.1.SL.TZ0.S_1c:
Find the sum of the first terms.
-
19N.2.SL.TZ0.S_5a:
Find the value of .
-
SPM.1.AHL.TZ0.11c:
Find the area of triangle UVW.
-
18M.1.AHL.TZ1.H_11a.i:
Express w2 and w3 in modulus-argument form.
-
18M.1.SL.TZ2.T_5a.ii:
Write down the amount of interest he earned after 5 years.
-
18M.1.AHL.TZ2.H_10b.i:
Express in the form where A, B are constants.
-
16N.1.AHL.TZ0.H_10a:
Show that .
-
20N.1.AHL.TZ0.H_12a:
State the equation of the vertical asymptote on the graph of .
-
20N.1.AHL.TZ0.H_12d:
Sketch the graph of , stating clearly the equations of any asymptotes and the coordinates of any points of intersections with the coordinate axes.
-
20N.3.AHL.TZ0.Hdm_3b.ii:
The base number is divisible by . Find the possible values of the digit .
-
EXN.1.SL.TZ0.4a:
Show that .
-
EXN.2.SL.TZ0.7b:
Given that follows a geometric sequence, state the value of the common ratio, .
-
EXN.3.AHL.TZ0.2j:
Use proof by contradiction to prove that a prime number, , that is not of the form is a Gaussian prime.
-
21M.1.SL.TZ1.2b:
The volume of the planet can be expressed in the form where and .
Find the value of and the value of .
-
21M.1.SL.TZ2.2:
Consider two consecutive positive integers, and .
Show that the difference of their squares is equal to the sum of the two integers.
-
21M.2.SL.TZ2.9c:
Given that the grand prize is not won and the grand prize continues to double, write an expression in terms of for the value of the grand prize in the week of the lottery.
-
21M.1.AHL.TZ2.12d:
Using mathematical induction and the result from part (b), prove that for .
-
21M.3.AHL.TZ2.2g.ii:
Hence, using the part (g)(i) and part (f) results, or otherwise, prove your suggested result to part (e).
-
21N.1.SL.TZ0.8b:
Write down an expression for .
-
21N.1.AHL.TZ0.12a.ii:
Find and , expressing these in the form , where and .
-
21N.1.AHL.TZ0.12e:
Determine the value of .
-
21N.2.AHL.TZ0.6a:
Prove the identity .
-
21N.3.AHL.TZ0.1e:
Show that .
-
21N.3.AHL.TZ0.1d:
Hence find, and simplify, an expression for .
-
22M.3.AHL.TZ1.1c:
Show that is the square of an odd number for all .
-
22M.3.AHL.TZ2.2e.ii:
Explain why the equation will have at least one real root for all values of .
-
22M.1.SL.TZ1.5:
Consider the curve with equation , where and .
The tangent to the curve at the point where is parallel to the line .
Find the value of .
-
22M.1.SL.TZ2.2c:
Find the common difference, .
-
22M.1.AHL.TZ1.11a:
Show that the three planes do not intersect.
-
EXM.1.AHL.TZ0.3c:
Use part (a) to find the exact value of , giving the answer in the form , .
-
EXM.1.SL.TZ0.1a:
Explain why any integer can be written in the form or or or , where .
-
EXM.3.AHL.TZ0.1e:
Hence, by recognising the pattern, deduce the first four terms in a power series for , .
-
EXM.3.AHL.TZ0.1d:
Repeat this process to find the first four terms in a power series for .
-
EXM.3.AHL.TZ0.4f:
Given that the initial population is 1000, and , find the number of years it will take for the population to triple.
-
19M.2.SL.TZ1.S_7b.i:
Find the value of .
-
18M.2.AHL.TZ1.H_7b:
Find the approximate number of fish in the lake at the start of 2042.
-
17N.2.SL.TZ0.T_2a.i:
Write down the distance Rosa runs in the third training session;
-
17N.2.SL.TZ0.T_2a.ii:
Write down the distance Rosa runs in the th training session.
-
18M.1.AHL.TZ2.H_11a:
Show that where .
-
19M.2.SL.TZ2.S_10d:
An infinite geometric series is given as , .
Find the largest value of such that .
-
17M.1.SL.TZ2.T_5a:
Diagram is formed with 52 sticks. Find the value of .
-
17M.1.SL.TZ2.T_9b:
Find the value of .
-
17M.1.SL.TZ2.T_9c:
Find the smallest value of for which is less than .
-
17M.1.AHL.TZ1.H_7a:
find the value of .
-
19M.1.SL.TZ1.S_10d:
The following diagram shows part of the graph of reflected in the -axis. It also shows part of the graph of and the point P.
Find an expression for the area of the shaded region. Do not calculate the value of the expression.
-
17N.1.AHL.TZ0.H_10b.ii:
Determine the variance of X.
-
17N.1.AHL.TZ0.H_1:
Solve the equation .
-
17M.1.AHL.TZ2.H_11b:
Show that .
-
18M.2.SL.TZ1.S_8c:
The relationship between x and y can be modelled using the formula y = kxn, where k ≠ 0 , n ≠ 0 , n ≠ 1.
By expressing ln y in terms of ln x, find the value of n and of k.
-
19M.2.AHL.TZ2.H_8a:
Find the roots of the equation , . Give your answers in Cartesian form.
-
16N.1.AHL.TZ0.H_12c:
Find the values of that satisfy the equation .
-
16N.1.AHL.TZ0.H_12d:
Solve the inequality .
-
18M.2.AHL.TZ2.H_1c:
Find the argument of , giving your answer to 4 decimal places.
-
17M.1.AHL.TZ1.H_2b:
Find the smallest positive integer value of , such that is a real number.
-
19M.1.AHL.TZ1.H_11b:
Verify that is the point of intersection of the two lines.
-
17M.1.SL.TZ1.T_2c:
Write down your answer to part (b) in the form where and k .
-
19N.1.AHL.TZ0.H_5a:
Solve the equation, giving the solutions in the form , where .
-
19N.2.AHL.TZ0.H_10c.ii:
.
-
19N.2.AHL.TZ0.H_10c.iii:
the median of .
-
19N.2.SL.TZ0.S_5c:
Find the least value of such that .
-
17M.2.AHL.TZ1.H_3:
The coefficient of in the expansion of is equal to the coefficient of in the expansion of . Find the value of .
-
18M.1.AHL.TZ1.H_11c:
Let . The points represented on an Argand diagram by form the vertices of a polygon .
Show that the area of the polygon can be expressed in the form , where .
-
17N.2.AHL.TZ0.H_12c:
Given that Phil’s aim is to own the house after 20 years, find the value for to the nearest dollar.
-
EXM.3.AHL.TZ0.2h:
Find the total area of this sided polygon.
-
17N.2.AHL.TZ0.H_12a:
Find the amount Phil would owe the bank after 20 years. Give your answer to the nearest dollar.
-
20N.1.AHL.TZ0.H_12c:
Use an algebraic method to determine whether is a self-inverse function.
-
20N.2.AHL.TZ0.H_11a:
Find the times when comes to instantaneous rest.
-
20N.1.SL.TZ0.T_15a:
Find the common ratio of the sequence.
-
20N.1.SL.TZ0.T_8a:
Calculate the value of Imon’s investment after years.
-
20N.2.SL.TZ0.T_5e.i:
Find the value of such that .
-
EXN.2.SL.TZ0.7c.i:
Find the value of .
-
21M.2.SL.TZ1.7c.i:
Show that Chris will never reach the target if his initial deposit is .
-
21M.1.AHL.TZ1.12b:
Use mathematical induction to prove that for .
-
21M.2.AHL.TZ1.12a:
The expression for can be written in the form , where . Find and in terms of .
-
21M.3.AHL.TZ2.2d:
Show that .
-
21M.3.AHL.TZ2.2g.i:
Express as a product of linear factors over the set .
-
21M.2.SL.TZ2.3a:
Given that the th term of the sequence is zero, find the value of .
-
21N.1.AHL.TZ0.3:
Solve the equation , where .
-
21N.3.AHL.TZ0.1g:
The hyperbola with equation can be rotated to coincide with the curve defined by .
Find the possible values of .
-
21N.3.AHL.TZ0.2b.ii:
By substituting , show that where is a constant.
-
21N.3.AHL.TZ0.1f:
Sketch the graph of , stating the coordinates of any axis intercepts and the equation of each asymptote.
-
22M.3.AHL.TZ1.1b.i:
Show that .
-
22M.3.AHL.TZ2.2e.i:
By varying the value of in the equation , determine the smallest positive integer value of required to show that Noah is incorrect.
-
22M.3.AHL.TZ2.2b.ii:
Hence show that .
-
22M.1.SL.TZ1.8a.ii:
Given that and , find the value of .
-
22M.2.AHL.TZ1.9b:
Find the number of ways these five people can now be seated in this row.
-
22M.1.SL.TZ1.8b.i:
Show that .
-
22M.1.AHL.TZ1.6:
Consider the expansion of where . Determine all possible values of for which the expansion has a non-zero constant term.
-
22M.1.AHL.TZ1.11b.i:
Verify that the point lies on both and .
-
22M.2.SL.TZ2.3a:
Find Gemma’s annual salary for the year 2021, to the nearest dollar.
-
22M.2.AHL.TZ2.12e:
By solving the logistic differential equation, show that its solution can be expressed in the form
.
-
SPM.1.SL.TZ0.6a:
Show that .
-
EXM.1.AHL.TZ0.3a:
Express in partial fractions.
-
EXM.3.AHL.TZ0.1a:
Expand using the Binomial Theorem.
-
EXM.3.AHL.TZ0.1h:
Repeat this procedure to find and .
-
EXM.3.AHL.TZ0.4c.i:
the solution of the differential equation, giving your answer in the form .
-
EXM.3.AHL.TZ0.4d:
Show that , where .
-
17N.2.SL.TZ0.T_2d:
Find the distance Carlos runs in the fifth month of training.
-
16N.1.AHL.TZ0.H_13d:
Hence or otherwise solve the equation in the interval .
-
18M.1.AHL.TZ1.H_5:
Solve .
-
19M.2.SL.TZ2.S_10c:
Show that .
-
16N.1.SL.TZ0.T_13b:
Determine how many times the comet has been seen from Earth up to the year 2014.
-
19M.1.SL.TZ1.S_10c:
At point P, the graphs of and intersect for the 21st time. Find the coordinates of P.
-
17M.1.SL.TZ2.T_1b.i:
Write down your answer to part (a) correct to two decimal places;
-
17M.1.SL.TZ2.T_1b.ii:
Write down your answer to part (a) correct to three significant figures.
-
17N.1.AHL.TZ0.H_11b:
By using mathematical induction, prove that
where .
-
19M.2.SL.TZ1.T_5b:
Find the value of the bicycle during the 5th year. Give your answer to two decimal places.
-
19M.2.SL.TZ2.T_6c:
After complete months Tommaso will, for the first time, have enough money in his account to buy the bicycle.
Find the value of .
-
17M.1.AHL.TZ2.H_11c.i:
Find the modulus and argument of in terms of . Express each answer in its simplest form.
-
19M.2.AHL.TZ1.H_2a:
where , , .
-
18N.1.SL.TZ0.T_1a:
Calculate the volume of this hemisphere in cm3.
Give your answer correct to one decimal place.
-
19N.2.AHL.TZ0.H_10c.i:
.
-
19N.2.AHL.TZ0.H_5:
Consider the expansion of , where and .
The coefficient of is four times the coefficient of . Find the value of .
-
19N.2.AHL.TZ0.H_6:
Let , where and .
One of the roots of is . Find the value of .
-
19N.2.AHL.TZ0.H_8b:
the girls do not sit on either end.
-
19N.1.SL.TZ0.S_10c:
The line is tangent to the graph of at and has equation .
The line passes through the point .
The gradient of the normal to at is .
Find the equation of in terms of .
-
19N.2.SL.TZ0.S_5b:
Find the value of .
-
18N.2.AHL.TZ0.H_1b:
Find the sum to infinity of this sequence.
-
17M.1.SL.TZ2.T_14a:
Write down the amount of money Jashanti saves per month.
-
19M.2.AHL.TZ2.H_9b:
Sketch the graph of , stating clearly the coordinates of any maximum and minimum points and intersections with axes.
Sub sections and their related questions
SL 1.1—Using standard form
-
19M.1.SL.TZ2.T_1a:
Use this model to calculate the circumference of the Moon in kilometres. Give your full calculator display.
-
19M.1.SL.TZ2.T_1b:
Give your answer to part (a) correct to three significant figures.
-
19M.1.SL.TZ2.T_1c:
Write your answer to part (b) in the form , where 1 ≤ < 10 , .
-
16N.1.SL.TZ0.T_1a:
Calculate the value of . Write down your full calculator display.
-
16N.1.SL.TZ0.T_1b:
Write your answer to part (a)
(i) correct to two decimal places;
(ii) correct to three significant figures.
-
16N.1.SL.TZ0.T_1c:
Write your answer to part (b)(ii) in the form , where .
-
18N.1.SL.TZ0.T_1a:
Calculate the volume of this hemisphere in cm3.
Give your answer correct to one decimal place.
-
18N.1.SL.TZ0.T_1b:
Write down your answer to part (a) correct to the nearest integer.
-
18N.1.SL.TZ0.T_1c:
Write down your answer to part (b) in the form a × 10k , where 1 ≤ a < 10 and k ∈ .
-
17N.1.SL.TZ0.T_3a:
Calculate the time, in minutes, it takes for light from the Sun to reach the Earth.
-
17N.1.SL.TZ0.T_3b:
Find the distance from the Earth to Polaris in millions of km. Give your answer in the form with and .
-
18M.1.SL.TZ2.T_3a:
Find the length, in cm, of this line. Give your answer in the form a × 10k , where 1 ≤ a < 10 and k ∈ .
-
18M.1.SL.TZ2.T_3b.i:
Write down the length of the Amazon River in cm.
-
18M.1.SL.TZ2.T_3b.ii:
Find the value of x.
-
17M.1.SL.TZ1.T_2a:
Calculate the percentage of the population of Ottawa that speak English but not French.
-
17M.1.SL.TZ1.T_2b:
Calculate the number of people in Ottawa that speak both English and French.
-
17M.1.SL.TZ1.T_2c:
Write down your answer to part (b) in the form where and k .
-
17M.1.SL.TZ2.T_1a:
Calculate . Give your full calculator display.
-
17M.1.SL.TZ2.T_1b.i:
Write down your answer to part (a) correct to two decimal places;
-
17M.1.SL.TZ2.T_1b.ii:
Write down your answer to part (a) correct to three significant figures.
-
17M.1.SL.TZ2.T_1c:
Write your answer to part (b)(ii) in the form , where .
-
20N.1.SL.TZ0.T_1a:
Write down the value of the iron in the form where .
-
20N.1.SL.TZ0.T_1b:
Calculate James’s estimate of its volume, in .
-
20N.1.SL.TZ0.T_1c:
The actual volume of the asteroid is found to be .
Find the percentage error in James’s estimate of the volume.
-
21M.1.SL.TZ1.2a:
Write down the radius of the planet.
-
21M.1.SL.TZ1.2b:
The volume of the planet can be expressed in the form where and .
Find the value of and the value of .
SL 1.2—Arithmetic sequences and series
-
19M.1.SL.TZ1.S_10a:
Find the two smallest non-zero values of for which .
-
19M.1.SL.TZ1.S_10c:
At point P, the graphs of and intersect for the 21st time. Find the coordinates of P.
-
19M.1.SL.TZ1.S_10d:
The following diagram shows part of the graph of reflected in the -axis. It also shows part of the graph of and the point P.
Find an expression for the area of the shaded region. Do not calculate the value of the expression.
-
19M.2.SL.TZ1.T_5a:
Calculate, in CAD, the total amount John pays for the bicycle.
-
19M.2.SL.TZ1.T_5b:
Find the value of the bicycle during the 5th year. Give your answer to two decimal places.
-
19M.2.SL.TZ1.T_5c:
Calculate, in years, when the bicycle value will be less than 50 USD.
-
19M.2.SL.TZ1.T_5d:
Find the total amount John has paid to insure his bicycle for the first 5 years.
-
19M.2.SL.TZ1.T_5e:
John purchased the bicycle in 2008.
Justify why John should not insure his bicycle in 2019.
-
17M.1.AHL.TZ1.H_7a:
find the value of .
-
17M.1.AHL.TZ1.H_7b:
determine the value of .
-
17M.1.AHL.TZ2.H_3a:
the value of ;
-
17M.1.AHL.TZ2.H_3b:
the value of ;
-
18M.2.AHL.TZ1.H_1b:
Calculate the number of positive terms in the sequence.
-
18M.2.AHL.TZ1.H_7a:
Show that there will be approximately 2645 fish in the lake at the start of 2020.
-
18M.2.AHL.TZ1.H_7b:
Find the approximate number of fish in the lake at the start of 2042.
-
18N.2.AHL.TZ0.H_1a:
Find the common ratio of this sequence.
-
17N.1.SL.TZ0.S_2a:
Find the common difference.
-
17N.1.SL.TZ0.S_2b:
Find the tenth term.
-
17M.1.SL.TZ2.S_1a:
Find the common difference.
-
17M.1.SL.TZ2.S_1b:
Find the tenth term.
-
17M.1.SL.TZ2.S_1c:
Find the sum of the first ten terms of the sequence.
-
18M.2.SL.TZ1.S_7a:
Given that xk + 1 = xk + a, find a.
-
18M.2.SL.TZ1.S_7b:
Hence find the value of n such that .
-
19M.2.SL.TZ2.S_10b:
Find the exact value of .
-
19M.2.SL.TZ2.S_10c:
Show that .
-
19M.2.SL.TZ2.S_10d:
An infinite geometric series is given as , .
Find the largest value of such that .
-
18N.1.SL.TZ0.S_3a:
Find u8.
-
19M.2.SL.TZ1.S_7b.ii:
Find the value of .
-
17N.2.SL.TZ0.T_2a.i:
Write down the distance Rosa runs in the third training session;
-
17N.2.SL.TZ0.T_2a.ii:
Write down the distance Rosa runs in the th training session.
-
17N.2.SL.TZ0.T_2b:
Find the value of .
-
17N.2.SL.TZ0.T_2c:
Calculate the total distance, in kilometres, Rosa runs in the first 50 training sessions.
-
17N.2.SL.TZ0.T_2d:
Find the distance Carlos runs in the fifth month of training.
-
17N.2.SL.TZ0.T_2e:
Calculate the total distance Carlos runs in the first year.
-
18M.1.SL.TZ1.T_7a.i:
For that day find how much weight was added after each lift.
-
18M.1.SL.TZ1.T_7a.ii:
For that day find the weight of Sergei’s first lift.
-
18M.1.SL.TZ1.T_7b:
On that day, Sergei made 12 successive lifts. Find the total combined weight of these lifts.
-
18M.2.SL.TZ2.T_4b:
Calculate the café’s total profit for the first 12 weeks.
-
18M.2.SL.TZ2.T_4d:
Calculate the tea-shop’s total profit for the first 12 weeks.
-
17M.1.SL.TZ2.T_5a:
Diagram is formed with 52 sticks. Find the value of .
-
17M.1.SL.TZ2.T_5b:
Find the total number of sticks used by Tomás for all 24 diagrams.
-
17M.1.SL.TZ1.T_5a:
Find the distance from the base of this ladder to the top rung.
-
17M.1.SL.TZ1.T_5b:
The company also makes a ladder that is 1050 cm long.
Find the maximum number of rungs in this 1050 cm long ladder.
-
16N.1.SL.TZ0.T_13a:
Find the year in which the comet was seen from Earth for the fifth time.
-
16N.1.SL.TZ0.T_13b:
Determine how many times the comet has been seen from Earth up to the year 2014.
-
19N.1.SL.TZ0.S_1a:
Find the common difference.
-
19N.1.SL.TZ0.S_1b:
Find the first term.
-
19N.1.SL.TZ0.S_1c:
Find the sum of the first terms.
-
20N.2.SL.TZ0.T_5a:
Find , the height of the tank.
-
20N.2.SL.TZ0.T_5b:
Show that the volume of the tank is , correct to three significant figures.
-
20N.2.SL.TZ0.T_5c:
Write down the common difference, .
-
20N.2.SL.TZ0.T_5d:
Find the amount of fuel pumped into the tank in the hour.
-
20N.2.SL.TZ0.T_5e.i:
Find the value of such that .
-
20N.2.SL.TZ0.T_5e.ii:
Write down the number of hours that the pump was pumping fuel into the tank.
-
20N.2.SL.TZ0.T_5f:
Find the total amount of fuel pumped into the tank in the first hours.
-
20N.2.SL.TZ0.T_5g:
Show that the tank will never be completely filled using this pump.
-
EXN.1.SL.TZ0.4a:
Show that .
-
EXN.1.SL.TZ0.4b:
Prove that the sum of the first terms of this arithmetic sequence is a square number.
-
EXN.2.SL.TZ0.7a:
Show that .
-
EXN.2.SL.TZ0.7b:
Given that follows a geometric sequence, state the value of the common ratio, .
-
EXN.2.SL.TZ0.7c.i:
Find the value of .
-
EXN.2.SL.TZ0.7c.ii:
For the value of found in part (c) (i), state Helen’s annual salary and Jane’s annual salary, correct to the nearest dollar.
-
EXN.2.SL.TZ0.7d:
Find Jane’s total earnings at the start of her th year of employment. Give your answer correct to the nearest dollar.
-
21M.1.SL.TZ1.3:
Consider an arithmetic sequence where . Find the value of the first term, , and the value of the common difference, .
-
21M.2.SL.TZ2.3a:
Given that the th term of the sequence is zero, find the value of .
-
21M.2.SL.TZ2.3b:
Let denote the sum of the first terms of the sequence.
Find the maximum value of .
-
21N.1.SL.TZ0.8a:
Show that .
-
21N.1.SL.TZ0.8b:
Write down an expression for .
-
21N.1.SL.TZ0.8c:
Find the value of .
-
21N.1.SL.TZ0.8d.ii:
Find the value of and the value of .
-
21N.1.SL.TZ0.8d.i:
Show that and are four consecutive terms in a geometric sequence.
-
22M.3.AHL.TZ1.1d:
Hence show that for .
-
22M.3.AHL.TZ1.1e:
By using a suitable table of values or otherwise, determine the smallest positive integer, greater than , that is both a triangular number and a pentagonal number.
-
22M.1.SL.TZ1.8b.i:
Show that .
-
22M.1.SL.TZ1.8b.ii:
Write down in the form , where .
-
22M.1.AHL.TZ1.10b.i:
Show that .
-
22M.1.AHL.TZ1.10b.ii:
Write down in the form , where .
-
22M.1.AHL.TZ1.10b.iii:
The sum of the first terms of the series is .
Find the value of .
-
22M.1.SL.TZ2.2a:
State the value of the first term, .
-
22M.1.SL.TZ2.2b:
Given that the th term of this sequence is , find the value of .
-
22M.1.SL.TZ2.2c:
Find the common difference, .
-
19M.2.SL.TZ1.S_7a:
Write down the first three non-zero terms of .
-
19M.2.SL.TZ1.S_7b.i:
Find the value of .
SL 1.3—Geometric sequences and series
-
19M.2.SL.TZ1.T_5a:
Calculate, in CAD, the total amount John pays for the bicycle.
-
19M.2.SL.TZ1.T_5b:
Find the value of the bicycle during the 5th year. Give your answer to two decimal places.
-
19M.2.SL.TZ1.T_5c:
Calculate, in years, when the bicycle value will be less than 50 USD.
-
19M.2.SL.TZ1.T_5d:
Find the total amount John has paid to insure his bicycle for the first 5 years.
-
19M.2.SL.TZ1.T_5e:
John purchased the bicycle in 2008.
Justify why John should not insure his bicycle in 2019.
-
18N.2.AHL.TZ0.H_1b:
Find the sum to infinity of this sequence.
-
19M.2.AHL.TZ1.H_11a:
Show that .
-
19M.2.AHL.TZ1.H_11b:
Show that one of the real roots is equal to 1.
-
19M.2.AHL.TZ1.H_11c:
Given that , find the other two real roots.
-
16N.1.AHL.TZ0.H_10a:
Show that .
-
17M.1.SL.TZ1.S_7a:
Find the common ratio.
-
18M.2.SL.TZ2.S_4a:
Find the common ratio.
-
18M.2.SL.TZ2.S_4b:
Find the sum of the first 8 terms.
-
18M.2.SL.TZ2.S_4c:
Find the least value of n for which Sn > 163.
-
17N.1.SL.TZ0.S_10b:
The following diagram shows [CD], with length , where . Squares with side lengths , where , are drawn along [CD]. This process is carried on indefinitely. The diagram shows the first three squares.

The total sum of the areas of all the squares is . Find the value of .
-
18M.1.SL.TZ1.S_10a.i:
Find an expression for r in terms of θ.
-
18M.1.SL.TZ1.S_10c:
Find the values of θ which give the greatest value of the sum.
-
17M.2.SL.TZ2.S_5:
Consider a geometric sequence where the first term is 768 and the second term is 576.
Find the least value of such that the th term of the sequence is less than 7.
-
17N.2.SL.TZ0.T_2a.i:
Write down the distance Rosa runs in the third training session;
-
17N.2.SL.TZ0.T_2a.ii:
Write down the distance Rosa runs in the th training session.
-
17N.2.SL.TZ0.T_2b:
Find the value of .
-
17N.2.SL.TZ0.T_2c:
Calculate the total distance, in kilometres, Rosa runs in the first 50 training sessions.
-
17N.2.SL.TZ0.T_2d:
Find the distance Carlos runs in the fifth month of training.
-
17N.2.SL.TZ0.T_2e:
Calculate the total distance Carlos runs in the first year.
-
18M.2.SL.TZ2.T_4b:
Calculate the café’s total profit for the first 12 weeks.
-
18M.2.SL.TZ2.T_4d:
Calculate the tea-shop’s total profit for the first 12 weeks.
-
17M.1.SL.TZ2.T_9a:
Write down the common ratio of the sequence.
-
17M.1.SL.TZ2.T_9b:
Find the value of .
-
17M.1.SL.TZ2.T_9c:
Find the smallest value of for which is less than .
-
17M.1.SL.TZ1.T_10a:
Find the value of , the common ratio of the sequence.
-
17M.1.SL.TZ1.T_10b:
Find the value of for which .
-
17M.1.SL.TZ1.T_10c:
Find the sum of the first 30 terms of the sequence.
-
16N.1.SL.TZ0.T_10a:
Find the value of the common ratio for this sequence.
-
16N.1.SL.TZ0.T_10b:
Find the distance that the post is driven into the ground by the eighth strike of the hammer.
-
16N.1.SL.TZ0.T_10c:
Find the total depth that the post has been driven into the ground after 10 strikes of the hammer.
-
19N.2.AHL.TZ0.H_1:
A geometric sequence has and . Find the second term of the sequence.
-
19N.2.SL.TZ0.S_5a:
Find the value of .
-
19N.2.SL.TZ0.S_5b:
Find the value of .
-
19N.2.SL.TZ0.S_5c:
Find the least value of such that .
-
20N.1.AHL.TZ0.H_5:
The first term in an arithmetic sequence is and the fifth term is .
Find the common difference of the sequence, expressing your answer in the form , where .
-
20N.2.AHL.TZ0.H_11a:
Find the times when comes to instantaneous rest.
-
20N.2.AHL.TZ0.H_11b:
Find an expression for in terms of .
-
20N.2.AHL.TZ0.H_11c:
Find the maximum displacement of , in metres, from its initial position.
-
20N.2.AHL.TZ0.H_11d:
Find the total distance travelled by in the first seconds of its motion.
-
20N.2.AHL.TZ0.H_11e.i:
Show that, at these times, .
-
20N.2.AHL.TZ0.H_11e.ii:
Hence show that .
-
20N.1.SL.TZ0.T_15a:
Find the common ratio of the sequence.
-
20N.1.SL.TZ0.T_15b:
Find the volume of the smallest slice of pie.
-
20N.1.SL.TZ0.T_15c:
The apple pie has a volume of .
Find the total number of slices Mia can cut from this pie.
-
EXN.2.SL.TZ0.7a:
Show that .
-
EXN.2.SL.TZ0.7b:
Given that follows a geometric sequence, state the value of the common ratio, .
-
EXN.2.SL.TZ0.7c.i:
Find the value of .
-
EXN.2.SL.TZ0.7c.ii:
For the value of found in part (c) (i), state Helen’s annual salary and Jane’s annual salary, correct to the nearest dollar.
-
EXN.2.SL.TZ0.7d:
Find Jane’s total earnings at the start of her th year of employment. Give your answer correct to the nearest dollar.
-
21M.2.SL.TZ2.9c:
Given that the grand prize is not won and the grand prize continues to double, write an expression in terms of for the value of the grand prize in the week of the lottery.
-
21N.1.SL.TZ0.8a:
Show that .
-
21N.1.SL.TZ0.8b:
Write down an expression for .
-
21N.1.SL.TZ0.8c:
Find the value of .
-
21N.1.SL.TZ0.8d.ii:
Find the value of and the value of .
-
21N.1.SL.TZ0.8d.i:
Show that and are four consecutive terms in a geometric sequence.
-
21N.2.SL.TZ0.6a:
Find the first term of the sequence, .
-
21N.2.SL.TZ0.6b:
Find .
-
21N.2.SL.TZ0.6c:
Find the least value of such that .
-
22M.1.SL.TZ1.8a.i:
Show that .
-
22M.1.SL.TZ1.8a.ii:
Given that and , find the value of .
-
22M.1.AHL.TZ1.10a.i:
Show that .
-
22M.1.AHL.TZ1.10a.ii:
Hence or otherwise, show that the series is convergent.
-
22M.1.AHL.TZ1.10a.iii:
Given that and , find the value of .
-
22M.2.SL.TZ2.3a:
Find Gemma’s annual salary for the year 2021, to the nearest dollar.
SL 1.4—Financial apps – compound int, annual depreciation
-
SPM.2.SL.TZ0.3a:
Find the value of r, giving your answer to four significant figures.
-
SPM.2.SL.TZ0.3b:
Laurie makes no further deposits to or withdrawals from the account.
Find the year in which the amount of money in Laurie’s account will become double the amount she invested.
-
18M.1.SL.TZ2.T_5a.i:
Calculate the amount of money he has in the account after 5 years.
-
18M.1.SL.TZ2.T_5a.ii:
Write down the amount of interest he earned after 5 years.
-
18M.1.SL.TZ2.T_5b:
Karl decides to donate this interest to a charity in France. The charity receives 170 euros (EUR). The exchange rate is 1 USD = t EUR.
Calculate the value of t.
-
17N.2.AHL.TZ0.H_12a:
Find the amount Phil would owe the bank after 20 years. Give your answer to the nearest dollar.
-
17N.2.AHL.TZ0.H_12b:
Show that the total value of Phil’s savings after 20 years is .
-
17N.2.AHL.TZ0.H_12c:
Given that Phil’s aim is to own the house after 20 years, find the value for to the nearest dollar.
-
17N.2.AHL.TZ0.H_12d.i:
David wishes to withdraw $5000 at the end of each year for a period of years. Show that an expression for the minimum value of is
.
-
17N.2.AHL.TZ0.H_12d.ii:
Hence or otherwise, find the minimum value of that would permit David to withdraw annual amounts of $5000 indefinitely. Give your answer to the nearest dollar.
-
17N.1.SL.TZ0.T_9a:
Calculate the original price of the bicycle.
-
17N.1.SL.TZ0.T_9b:
Calculate the difference between the original price of the bicycle and the total amount Juan will pay.
-
19M.2.SL.TZ2.T_6a:
Determine the amount that he will have in his account after 3 years. Give your answer correct to two decimal places.
-
19M.2.SL.TZ2.T_6b:
Find the difference between the cost of the bicycle and the amount of money in Tommaso’s account after 3 years. Give your answer correct to two decimal places.
-
19M.2.SL.TZ2.T_6c:
After complete months Tommaso will, for the first time, have enough money in his account to buy the bicycle.
Find the value of .
-
17M.1.SL.TZ2.T_14a:
Write down the amount of money Jashanti saves per month.
-
20N.1.SL.TZ0.T_8a:
Calculate the value of Imon’s investment after years.
-
20N.1.SL.TZ0.T_8b:
At the end of the years, Imon withdrew from the fixed deposit account and reinvested this into a super-savings account with a nominal annual interest rate of , compounded half-yearly.
The value of the super-savings account increased to after months.
Find the value of .
-
EXN.2.SL.TZ0.7a:
Show that .
-
EXN.2.SL.TZ0.7b:
Given that follows a geometric sequence, state the value of the common ratio, .
-
EXN.2.SL.TZ0.7c.i:
Find the value of .
-
EXN.2.SL.TZ0.7c.ii:
For the value of found in part (c) (i), state Helen’s annual salary and Jane’s annual salary, correct to the nearest dollar.
-
EXN.2.SL.TZ0.7d:
Find Jane’s total earnings at the start of her th year of employment. Give your answer correct to the nearest dollar.
-
21M.2.SL.TZ1.7a.i:
Find the value of Amelia’s investment after years to the nearest hundred dollars.
-
21M.2.SL.TZ1.7a.ii:
Determine the number of years required for Amelia’s investment to reach the target.
-
21M.2.SL.TZ1.7b:
Bill invests his in an account that offers an interest rate of per annum compounded monthly, where is set to two decimal places.
Find the minimum value of needed for Bill to reach the target after years.
-
21M.2.SL.TZ1.7c.i:
Show that Chris will never reach the target if his initial deposit is .
-
21M.2.SL.TZ1.7c.ii:
Find the amount Chris needs to deposit initially in order to reach the target after years. Give your answer to the nearest dollar.
-
22M.2.SL.TZ1.1a:
Find the amount that Sam will have in his account after years.
-
22M.2.SL.TZ1.1b:
Find the value of required so that the amount in David’s account after years will be equal to the amount in Sam’s account.
-
22M.2.SL.TZ1.1c:
Find the interest David will earn over the years.
-
22M.2.SL.TZ2.3a:
Find Gemma’s annual salary for the year 2021, to the nearest dollar.
SL 1.5—Intro to logs
-
17M.2.AHL.TZ2.H_6:
Given that , find in terms of .
-
18M.1.AHL.TZ2.H_11a:
Show that where .
-
19M.1.AHL.TZ2.H_7:
Solve the simultaneous equations
.
-
18M.1.AHL.TZ1.H_5:
Solve .
-
16N.1.AHL.TZ0.H_7:
Solve the equation .
-
17N.1.AHL.TZ0.H_1:
Solve the equation .
-
17M.1.AHL.TZ1.H_1:
Find the solution of .
-
18M.2.SL.TZ1.S_8a:
Find the value of a and of b.
-
18M.2.SL.TZ1.S_8b:
Use the regression equation to estimate the value of y when x = 3.57.
-
18M.2.SL.TZ1.S_8c:
The relationship between x and y can be modelled using the formula y = kxn, where k ≠ 0 , n ≠ 0 , n ≠ 1.
By expressing ln y in terms of ln x, find the value of n and of k.
-
19N.1.SL.TZ0.S_10a:
Write down the coordinates of .
-
19N.1.SL.TZ0.S_10b:
Given that , find the equation of in terms of , and .
-
19N.1.SL.TZ0.S_10c:
The line is tangent to the graph of at and has equation .
The line passes through the point .
The gradient of the normal to at is .
Find the equation of in terms of .
-
22M.1.SL.TZ2.8b:
Find the value of and the value of .
SL 1.6—Simple proof
-
SPM.1.SL.TZ0.3a:
Show that , where .
-
SPM.1.SL.TZ0.3b:
Hence, or otherwise, prove that the sum of the squares of any two consecutive odd integers is even.
-
EXM.1.SL.TZ0.1a:
Explain why any integer can be written in the form or or or , where .
-
EXM.1.SL.TZ0.1b:
Hence prove that the square of any integer can be written in the form or , where .
-
18M.1.AHL.TZ2.H_10b.i:
Express in the form where A, B are constants.
-
EXN.1.SL.TZ0.4a:
Show that .
-
EXN.1.SL.TZ0.4b:
Prove that the sum of the first terms of this arithmetic sequence is a square number.
-
EXN.3.AHL.TZ0.2h:
Show that .
-
21M.1.SL.TZ2.2:
Consider two consecutive positive integers, and .
Show that the difference of their squares is equal to the sum of the two integers.
-
21N.1.SL.TZ0.6a:
Show that .
-
21N.1.SL.TZ0.6b:
Hence or otherwise, solve the equation for .
-
21N.2.AHL.TZ0.6a:
Prove the identity .
-
21N.2.AHL.TZ0.6b:
The equation has two real roots, and .
Consider the equation , where and which has roots and .
Without solving , determine the values of and . -
21N.3.AHL.TZ0.1a:
Verify that satisfies the differential equation .
-
21N.3.AHL.TZ0.1b:
Show that .
-
21N.3.AHL.TZ0.1c.i:
.
-
21N.3.AHL.TZ0.1c.ii:
.
-
21N.3.AHL.TZ0.1d:
Hence find, and simplify, an expression for .
-
21N.3.AHL.TZ0.1e:
Show that .
-
21N.3.AHL.TZ0.1f:
Sketch the graph of , stating the coordinates of any axis intercepts and the equation of each asymptote.
-
21N.3.AHL.TZ0.1g:
The hyperbola with equation can be rotated to coincide with the curve defined by .
Find the possible values of .
-
21N.3.AHL.TZ0.2a.i:
By solving the differential equation , show that where is a constant.
-
21N.3.AHL.TZ0.2a.ii:
Show that .
-
21N.3.AHL.TZ0.2a.iii:
Solve the differential equation in part (a)(ii) to find as a function of .
-
21N.3.AHL.TZ0.2b.i:
By differentiating with respect to , show that .
-
21N.3.AHL.TZ0.2b.ii:
By substituting , show that where is a constant.
-
21N.3.AHL.TZ0.2b.iii:
Hence find as a function of .
-
21N.3.AHL.TZ0.2b.iv:
Hence show that , where is a constant.
-
21N.3.AHL.TZ0.2c.i:
Show that .
-
21N.3.AHL.TZ0.2c.ii:
Find the two values for that satisfy .
-
21N.3.AHL.TZ0.2c.iii:
Let the two values found in part (c)(ii) be and .
Verify that is a solution to the differential equation in (c)(i),where is a constant.
-
22M.3.AHL.TZ1.1a.i:
For triangular numbers, verify that .
-
22M.3.AHL.TZ1.1b.i:
Show that .
-
22M.3.AHL.TZ1.1b.ii:
State, in words, what the identity given in part (b)(i) shows for two consecutive triangular numbers.
-
22M.3.AHL.TZ1.1b.iii:
For , sketch a diagram clearly showing your answer to part (b)(ii).
-
22M.3.AHL.TZ1.1c:
Show that is the square of an odd number for all .
-
22M.3.AHL.TZ2.2a:
By expanding show that:
.
-
22M.3.AHL.TZ2.2b.i:
Show that .
-
22M.3.AHL.TZ2.2b.ii:
Hence show that .
-
22M.1.SL.TZ1.9a.ii:
By using a suitable substitution for , show that .
-
22M.1.SL.TZ2.3a:
Prove that the sum of these three integers is always divisible by .
-
22M.1.SL.TZ2.3b:
Prove that the sum of the squares of these three integers is never divisible by .
SL 1.7—Laws of exponents and logs
-
SPM.1.SL.TZ0.6a:
Show that .
-
SPM.1.SL.TZ0.6b:
Hence or otherwise solve for .
-
17M.2.AHL.TZ2.H_6:
Given that , find in terms of .
-
18M.1.AHL.TZ2.H_11a:
Show that where .
-
19M.1.AHL.TZ2.H_7:
Solve the simultaneous equations
.
-
18M.1.AHL.TZ1.H_5:
Solve .
-
16N.1.AHL.TZ0.H_7:
Solve the equation .
-
17N.1.AHL.TZ0.H_1:
Solve the equation .
-
17M.1.AHL.TZ1.H_1:
Find the solution of .
-
18M.2.SL.TZ1.S_8a:
Find the value of a and of b.
-
18M.2.SL.TZ1.S_8b:
Use the regression equation to estimate the value of y when x = 3.57.
-
18M.2.SL.TZ1.S_8c:
The relationship between x and y can be modelled using the formula y = kxn, where k ≠ 0 , n ≠ 0 , n ≠ 1.
By expressing ln y in terms of ln x, find the value of n and of k.
-
19N.1.AHL.TZ0.H_10d:
The area enclosed by the graph of and the line can be expressed as . Find the value of .
-
19N.3.AHL.TZ0.Hdm_2a.i:
State Fermat’s little theorem.
-
19N.3.AHL.TZ0.Hdm_2a.ii:
Find the remainder when is divided by .
-
19N.3.AHL.TZ0.Hdm_2b:
Convert to base , where .
-
19N.3.AHL.TZ0.Hdm_2c:
Consider the equation .
Find the value of .
-
20N.3.AHL.TZ0.Hdm_3a.i:
Write down the remainder when is divided by .
-
20N.3.AHL.TZ0.Hdm_3a.ii:
Use Fermat’s little theorem to find the remainder when is divided by .
-
20N.3.AHL.TZ0.Hdm_3b.i:
Prove that a number in base is divisible by if, and only if, the sum of its digits is divisible by .
-
20N.3.AHL.TZ0.Hdm_3b.ii:
The base number is divisible by . Find the possible values of the digit .
-
EXN.1.SL.TZ0.2:
Solve the equation . Give your answer in the form where .
-
21N.1.SL.TZ0.8a:
Show that .
-
21N.1.SL.TZ0.8b:
Write down an expression for .
-
21N.1.SL.TZ0.8c:
Find the value of .
-
21N.1.SL.TZ0.8d.ii:
Find the value of and the value of .
-
21N.1.SL.TZ0.8d.i:
Show that and are four consecutive terms in a geometric sequence.
-
21N.1.AHL.TZ0.3:
Solve the equation , where .
-
21N.2.AHL.TZ0.10a.i:
-axis.
-
21N.2.AHL.TZ0.10a.ii:
-axis.
-
21N.2.AHL.TZ0.10b:
Write down the equation of the vertical asymptote of the graph of .
-
21N.2.AHL.TZ0.10c:
The oblique asymptote of the graph of can be written as where .
Find the value of and the value of .
-
21N.2.AHL.TZ0.10d:
Sketch the graph of for , clearly indicating the points of intersection with each axis and any asymptotes.
-
21N.2.AHL.TZ0.10e.i:
Express in partial fractions.
-
21N.2.AHL.TZ0.10e.ii:
Hence find the exact value of , expressing your answer as a single logarithm.
-
22M.1.SL.TZ1.2a:
The expression can be written as . Write down the value of .
-
22M.1.SL.TZ1.5:
Consider the curve with equation , where and .
The tangent to the curve at the point where is parallel to the line .
Find the value of .
-
22M.1.SL.TZ1.8a.i:
Show that .
-
22M.1.SL.TZ1.8a.ii:
Given that and , find the value of .
-
22M.1.SL.TZ1.8b.i:
Show that .
-
22M.1.SL.TZ1.8b.ii:
Write down in the form , where .
-
22M.1.AHL.TZ1.1:
Find the value of .
-
22M.1.AHL.TZ1.10a.i:
Show that .
-
22M.1.AHL.TZ1.10a.ii:
Hence or otherwise, show that the series is convergent.
-
22M.1.AHL.TZ1.10a.iii:
Given that and , find the value of .
-
22M.1.AHL.TZ1.10b.i:
Show that .
-
22M.1.AHL.TZ1.10b.ii:
Write down in the form , where .
-
22M.1.AHL.TZ1.10b.iii:
The sum of the first terms of the series is .
Find the value of .
-
22M.1.SL.TZ2.8b:
Find the value of and the value of .
-
22M.2.AHL.TZ2.12e:
By solving the logistic differential equation, show that its solution can be expressed in the form
.
SL 1.8—Sum of infinite geo sequence
-
17N.1.SL.TZ0.S_10b:
The following diagram shows [CD], with length , where . Squares with side lengths , where , are drawn along [CD]. This process is carried on indefinitely. The diagram shows the first three squares.

The total sum of the areas of all the squares is . Find the value of .
-
18M.1.SL.TZ1.S_10a.i:
Find an expression for r in terms of θ.
-
18M.1.SL.TZ1.S_10c:
Find the values of θ which give the greatest value of the sum.
-
20N.2.SL.TZ0.S_6a:
Find the common ratio in terms of .
-
20N.2.SL.TZ0.S_6b:
Find the values of for which the sum to infinity of the series exists.
-
20N.2.SL.TZ0.S_6c:
Find the value of when .
-
EXN.2.AHL.TZ0.9:
A biased coin is weighted such that the probability, , of obtaining a tail is . The coin is tossed repeatedly and independently until a tail is obtained.
Let be the event “obtaining the first tail on an even numbered toss”.
Find .
-
21M.2.SL.TZ1.7c.i:
Show that Chris will never reach the target if his initial deposit is .
-
21N.2.SL.TZ0.6a:
Find the first term of the sequence, .
-
21N.2.SL.TZ0.6b:
Find .
-
21N.2.SL.TZ0.6c:
Find the least value of such that .
-
22M.1.SL.TZ1.8a.i:
Show that .
-
22M.1.SL.TZ1.8a.ii:
Given that and , find the value of .
-
22M.1.AHL.TZ1.10a.i:
Show that .
-
22M.1.AHL.TZ1.10a.ii:
Hence or otherwise, show that the series is convergent.
-
22M.1.AHL.TZ1.10a.iii:
Given that and , find the value of .
SL 1.9—Binomial theorem where n is an integer
-
17N.1.AHL.TZ0.H_10a:
Show that the probability that Chloe wins the game is .
-
17N.1.AHL.TZ0.H_10b.i:
Determine the mean of X.
-
17N.1.AHL.TZ0.H_10b.ii:
Determine the variance of X.
-
18M.2.AHL.TZ2.H_5a:
Express the binomial coefficient as a polynomial in .
-
18M.2.AHL.TZ2.H_5b:
Hence find the least value of for which .
-
17M.1.AHL.TZ1.H_4:
Three girls and four boys are seated randomly on a straight bench. Find the probability that the girls sit together and the boys sit together.
-
17M.2.AHL.TZ1.H_3:
The coefficient of in the expansion of is equal to the coefficient of in the expansion of . Find the value of .
-
17M.2.AHL.TZ2.H_8:
In a trial examination session a candidate at a school has to take 18 examination papers including the physics paper, the chemistry paper and the biology paper. No two of these three papers may be taken consecutively. There is no restriction on the order in which the other examination papers may be taken.
Find the number of different orders in which these 18 examination papers may be taken.
-
18N.1.AHL.TZ0.H_2a:
Find the number of different possible teams that could be chosen.
-
18N.1.AHL.TZ0.H_2b:
Find the number of different possible teams that could be chosen, given that the team must include at least one girl and at least one boy.
-
19M.1.AHL.TZ1.H_11a.ii:
Find how many sets of three points can be selected which can form the vertices of a triangle.
-
19M.1.AHL.TZ1.H_11b:
Verify that is the point of intersection of the two lines.
-
19M.1.AHL.TZ1.H_11c:
Write down the value of corresponding to the point .
-
19M.1.AHL.TZ1.H_11d:
Write down and .
-
19M.1.AHL.TZ1.H_11e:
Let be the point on with coordinates (1, 0, 1) and be the point on with parameter .
Find the area of the quadrilateral .
-
17M.2.SL.TZ1.S_6:
Let . Find the term in in the expansion of the derivative, .
-
19N.2.AHL.TZ0.H_5:
Consider the expansion of , where and .
The coefficient of is four times the coefficient of . Find the value of .
-
19N.2.AHL.TZ0.H_8a:
the girls do not sit together.
-
19N.2.AHL.TZ0.H_8b:
the girls do not sit on either end.
-
19N.2.AHL.TZ0.H_8c:
the girls do not sit on either end and do not sit together.
-
19N.1.SL.TZ0.S_4a:
Find the value of .
-
19N.1.SL.TZ0.S_4b:
Hence or otherwise find the coefficient of the term in in the expansion of .
-
20N.2.AHL.TZ0.H_4:
Find the term independent of in the expansion of .
-
20N.2.AHL.TZ0.H_7a:
There are more males than females in the group.
-
20N.2.AHL.TZ0.H_7b:
Two of the teachers, Gary and Gerwyn, refuse to go out for a meal together.
-
20N.2.SL.TZ0.S_5:
Consider the expansion of , where .
The coefficient of the term in is . Find the value of .
-
EXN.1.AHL.TZ0.12a:
Use the binomial theorem to expand . Give your answer in the form where and are expressed in terms of and .
-
21M.2.SL.TZ1.6:
Consider the expansion of , where .
Given that the coefficient of is , find the value of .
-
21M.1.SL.TZ2.4:
In the expansion of , where , the coefficient of the term in is .
Find the possible values of .
-
22M.1.SL.TZ1.9a.i:
Expand and simplify in ascending powers of .
-
22M.1.AHL.TZ1.6:
Consider the expansion of where . Determine all possible values of for which the expansion has a non-zero constant term.
-
22M.1.SL.TZ2.6a:
Show that .
-
22M.1.SL.TZ2.6b:
The third term in the expansion is the mean of the second term and the fourth term in the expansion.
Find the possible values of .
AHL 1.10—Perms and combs, binomial with negative and fractional indices
-
EXM.3.AHL.TZ0.1a:
Expand using the Binomial Theorem.
-
EXM.3.AHL.TZ0.1b:
Consider the power series
By considering the ratio of consecutive terms, explain why this series is equal to and state the values of for which this equality is true.
-
EXM.3.AHL.TZ0.1c:
Differentiate the equation obtained part (b) and hence, find the first four terms in a power series for .
-
EXM.3.AHL.TZ0.1d:
Repeat this process to find the first four terms in a power series for .
-
EXM.3.AHL.TZ0.1e:
Hence, by recognising the pattern, deduce the first four terms in a power series for , .
-
EXM.3.AHL.TZ0.1f:
By substituting , find the value of .
-
EXM.3.AHL.TZ0.1g:
By differentiating both sides of the expression and then substituting , find the value of .
-
EXM.3.AHL.TZ0.1h:
Repeat this procedure to find and .
-
EXM.3.AHL.TZ0.1i:
Hence, write down the first four terms in what is called the Extended Binomial Theorem for .
-
EXM.3.AHL.TZ0.1j:
Write down the power series for .
-
EXM.3.AHL.TZ0.1k:
Hence, using integration, find the power series for , giving the first four non-zero terms.
-
EXM.2.AHL.TZ0.1a:
Write down and simplify the first three terms, in ascending powers of , in the Extended Binomial expansion of .
-
EXM.2.AHL.TZ0.1b:
By substituting find a rational approximation to .
-
17N.1.AHL.TZ0.H_10a:
Show that the probability that Chloe wins the game is .
-
17N.1.AHL.TZ0.H_10b.i:
Determine the mean of X.
-
17N.1.AHL.TZ0.H_10b.ii:
Determine the variance of X.
-
18M.2.AHL.TZ2.H_5a:
Express the binomial coefficient as a polynomial in .
-
18M.2.AHL.TZ2.H_5b:
Hence find the least value of for which .
-
17M.1.AHL.TZ1.H_4:
Three girls and four boys are seated randomly on a straight bench. Find the probability that the girls sit together and the boys sit together.
-
17M.2.AHL.TZ2.H_8:
In a trial examination session a candidate at a school has to take 18 examination papers including the physics paper, the chemistry paper and the biology paper. No two of these three papers may be taken consecutively. There is no restriction on the order in which the other examination papers may be taken.
Find the number of different orders in which these 18 examination papers may be taken.
-
18N.1.AHL.TZ0.H_2a:
Find the number of different possible teams that could be chosen.
-
18N.1.AHL.TZ0.H_2b:
Find the number of different possible teams that could be chosen, given that the team must include at least one girl and at least one boy.
-
19M.1.AHL.TZ1.H_11a.i:
Find how many sets of four points can be selected which can form the vertices of a quadrilateral.
-
19M.1.AHL.TZ1.H_11a.ii:
Find how many sets of three points can be selected which can form the vertices of a triangle.
-
19M.1.AHL.TZ1.H_11b:
Verify that is the point of intersection of the two lines.
-
19M.1.AHL.TZ1.H_11c:
Write down the value of corresponding to the point .
-
19M.1.AHL.TZ1.H_11d:
Write down and .
-
19M.1.AHL.TZ1.H_11e:
Let be the point on with coordinates (1, 0, 1) and be the point on with parameter .
Find the area of the quadrilateral .
-
EXN.2.AHL.TZ0.7a:
Find the value of and the value of .
-
EXN.2.AHL.TZ0.7b:
Hence, expand in ascending powers of , up to and including the term in .
-
EXN.2.AHL.TZ0.7c:
Give a reason why the series expansion found in part (b) is not valid for .
-
21M.1.AHL.TZ1.9a:
Each pen is large enough to contain five sheep. Amber and Brownie must not be placed in the same pen.
-
21M.1.AHL.TZ1.9b:
Each pen may only contain one sheep. Amber and Brownie must not be placed in pens which share a boundary.
-
21M.2.AHL.TZ2.7a:
in the position immediately after Andrea.
-
21M.2.AHL.TZ2.7b:
in any position after Andrea.
-
21M.2.AHL.TZ2.9a:
Write down the first three terms of the binomial expansion of in ascending powers of .
-
21N.1.AHL.TZ0.9a:
Find the value of and the value of .
-
21N.1.AHL.TZ0.9b:
State the restriction which must be placed on for this expansion to be valid.
-
22M.1.AHL.TZ1.6:
Consider the expansion of where . Determine all possible values of for which the expansion has a non-zero constant term.
-
22M.2.AHL.TZ1.9a:
Find the number of ways these five people can be seated in this row.
-
22M.2.AHL.TZ1.9b:
Find the number of ways these five people can now be seated in this row.
-
22M.2.AHL.TZ2.9a:
the digits are distinct.
-
22M.2.AHL.TZ2.9b:
the digits are distinct and are in increasing order.
AHL 1.11—Partial fractions
-
EXM.1.AHL.TZ0.1:
Let for . Use partial fractions to find .
-
EXM.1.AHL.TZ0.2a:
Very briefly, explain why the value of this integral must be negative.
-
EXM.1.AHL.TZ0.2b:
Express the function in partial fractions.
-
EXM.1.AHL.TZ0.2c:
Use parts (a) and (b) to show that .
-
EXM.1.AHL.TZ0.3a:
Express in partial fractions.
-
EXM.1.AHL.TZ0.3b:
Use part (a) to show that is always decreasing.
-
EXM.1.AHL.TZ0.3c:
Use part (a) to find the exact value of , giving the answer in the form , .
-
EXM.3.AHL.TZ0.4a:
Show that the general solution of this differential equation is , where .
-
EXM.3.AHL.TZ0.4b.i:
the population after 10 years
-
EXM.3.AHL.TZ0.4b.ii:
the number of years it will take for the population to triple.
-
EXM.3.AHL.TZ0.4b.iii:
-
EXM.3.AHL.TZ0.4c.i:
the solution of the differential equation, giving your answer in the form .
-
EXM.3.AHL.TZ0.4c.ii:
the number of years it will take for the population to triple.
-
EXM.3.AHL.TZ0.4d:
Show that , where .
-
EXM.3.AHL.TZ0.4e:
Solve the differential equation , giving your answer in the form .
-
EXM.3.AHL.TZ0.4f:
Given that the initial population is 1000, and , find the number of years it will take for the population to triple.
-
18N.2.AHL.TZ0.H_1b:
Find the sum to infinity of this sequence.
-
19N.1.AHL.TZ0.H_10c:
Show that .
-
19N.1.AHL.TZ0.H_10d:
The area enclosed by the graph of and the line can be expressed as . Find the value of .
-
19N.2.AHL.TZ0.H_11b:
Find the area of .
-
19N.2.AHL.TZ0.H_11c:
The region is now rotated about the -axis, through radians, to form a solid.
By writing as , show that the volume of the solid formed is .
-
20N.1.AHL.TZ0.H_12a:
State the equation of the vertical asymptote on the graph of .
-
20N.1.AHL.TZ0.H_12b:
State the equation of the horizontal asymptote on the graph of .
-
20N.1.AHL.TZ0.H_12c:
Use an algebraic method to determine whether is a self-inverse function.
-
20N.1.AHL.TZ0.H_12d:
Sketch the graph of , stating clearly the equations of any asymptotes and the coordinates of any points of intersections with the coordinate axes.
-
20N.1.AHL.TZ0.H_12e:
The region bounded by the -axis, the curve , and the lines and is rotated through about the -axis. Find the volume of the solid generated, giving your answer in the form , where .
-
20N.2.AHL.TZ0.H_3a:
Determine the values of , and .
-
20N.2.AHL.TZ0.H_3b:
Hence find the area of the shaded region.
-
EXN.2.AHL.TZ0.7a:
Find the value of and the value of .
-
EXN.2.AHL.TZ0.7b:
Hence, expand in ascending powers of , up to and including the term in .
-
EXN.2.AHL.TZ0.7c:
Give a reason why the series expansion found in part (b) is not valid for .
-
21M.2.AHL.TZ1.12a:
The expression for can be written in the form , where . Find and in terms of .
-
21M.2.AHL.TZ1.12b:
Hence, find an expression for .
-
21N.2.AHL.TZ0.10a.i:
-axis.
-
21N.2.AHL.TZ0.10a.ii:
-axis.
-
21N.2.AHL.TZ0.10b:
Write down the equation of the vertical asymptote of the graph of .
-
21N.2.AHL.TZ0.10c:
The oblique asymptote of the graph of can be written as where .
Find the value of and the value of .
-
21N.2.AHL.TZ0.10d:
Sketch the graph of for , clearly indicating the points of intersection with each axis and any asymptotes.
-
21N.2.AHL.TZ0.10e.i:
Express in partial fractions.
-
21N.2.AHL.TZ0.10e.ii:
Hence find the exact value of , expressing your answer as a single logarithm.
-
22M.2.AHL.TZ1.12c.i:
By solving the differential equation, show that .
-
22M.2.AHL.TZ1.12c.ii:
Find the actual value of when .
-
22M.2.AHL.TZ2.12e:
By solving the logistic differential equation, show that its solution can be expressed in the form
.
AHL 1.12—Complex numbers – Cartesian form and Argand diag
-
SPM.2.AHL.TZ0.8:
The complex numbers and satisfy the equations
.
Find and in the form where , .
-
16N.1.AHL.TZ0.H_12a:
Determine the value of
(i) ;
(ii) .
-
16N.1.AHL.TZ0.H_12b:
Show that .
-
16N.1.AHL.TZ0.H_12c:
Find the values of that satisfy the equation .
-
16N.1.AHL.TZ0.H_12d:
Solve the inequality .
-
17M.1.AHL.TZ2.H_5:
In the following Argand diagram the point A represents the complex number and the point B represents the complex number . The shape of ABCD is a square. Determine the complex numbers represented by the points C and D.

-
19N.1.AHL.TZ0.H_5b:
The solutions form the vertices of a polygon in the complex plane. Find the area of the polygon.
-
20N.1.AHL.TZ0.H_4:
Consider the equation , where and .
Find the value of and the value of .
-
EXN.1.AHL.TZ0.12a:
Use the binomial theorem to expand . Give your answer in the form where and are expressed in terms of and .
-
21M.2.AHL.TZ2.8:
Consider where .
Show that .
-
21M.3.AHL.TZ2.2a.i:
Show that .
-
21M.3.AHL.TZ2.2a.ii:
Hence, deduce that .
-
21M.3.AHL.TZ2.2b:
Show that .
-
21M.3.AHL.TZ2.2c:
By factorizing , or otherwise, deduce that .
-
21M.3.AHL.TZ2.2d:
Show that .
-
21M.3.AHL.TZ2.2e:
Suggest a value for .
-
21M.3.AHL.TZ2.2f.i:
Write down expressions for and in terms of .
-
21M.3.AHL.TZ2.2f.ii:
Hence, write down an expression for in terms of and .
-
21M.3.AHL.TZ2.2g.i:
Express as a product of linear factors over the set .
-
21M.3.AHL.TZ2.2g.ii:
Hence, using the part (g)(i) and part (f) results, or otherwise, prove your suggested result to part (e).
-
21N.1.AHL.TZ0.12a.i:
Verify that is a root of this equation.
-
21N.1.AHL.TZ0.12a.ii:
Find and , expressing these in the form , where and .
-
21N.1.AHL.TZ0.12b:
Plot the points , and on an Argand diagram.
-
21N.1.AHL.TZ0.12c:
Find .
-
21N.1.AHL.TZ0.12d:
By using de Moivre’s theorem, show that is a root of this equation.
-
21N.1.AHL.TZ0.12e:
Determine the value of .
-
21N.3.AHL.TZ0.1a:
Verify that satisfies the differential equation .
-
21N.3.AHL.TZ0.1b:
Show that .
-
21N.3.AHL.TZ0.1c.i:
.
-
21N.3.AHL.TZ0.1c.ii:
.
-
21N.3.AHL.TZ0.1d:
Hence find, and simplify, an expression for .
-
21N.3.AHL.TZ0.1e:
Show that .
-
21N.3.AHL.TZ0.1f:
Sketch the graph of , stating the coordinates of any axis intercepts and the equation of each asymptote.
-
21N.3.AHL.TZ0.1g:
The hyperbola with equation can be rotated to coincide with the curve defined by .
Find the possible values of .
-
22M.3.AHL.TZ1.2e:
Deduce from part (d)(i) that the complex roots of the equation can be expressed as .
-
22M.3.AHL.TZ1.2f.i:
Use this diagram to determine the roots of the corresponding equation of the form for .
-
22M.3.AHL.TZ1.2f.ii:
State the coordinates of .
-
22M.1.AHL.TZ1.9a:
Find an expression for in terms of .
-
22M.1.AHL.TZ2.12a:
Show that where is the complex conjugate of .
-
22M.1.AHL.TZ2.12b:
Given that , show that is a right-angled triangle.
-
22M.1.AHL.TZ2.12c.i:
Express in terms of .
-
22M.1.AHL.TZ2.12c.ii:
Hence show that .
-
22M.1.AHL.TZ2.12d:
Use the result from part (c)(ii) to show that .
-
22M.1.AHL.TZ2.12e:
Consider the equation , where and .
Given that , deduce that only one equilateral triangle can be formed from the point and the roots of this equation.
AHL 1.13—Polar and Euler form
-
SPM.1.AHL.TZ0.11a:
Express in the form , where and .
-
SPM.1.AHL.TZ0.11b:
Find , and expressing your answers in the form , where and .
-
SPM.1.AHL.TZ0.11c:
Find the area of triangle UVW.
-
SPM.1.AHL.TZ0.11d:
By considering the sum of the roots , and , show that
.
-
EXM.3.AHL.TZ0.2a:
By considering the area of two triangles and the area of the sector show that .
-
EXM.3.AHL.TZ0.2b:
Hence show that .
-
EXM.3.AHL.TZ0.2c:
Let . Working in modulus/argument form find the solutions to this equation.
-
EXM.3.AHL.TZ0.2d:
Represent these solutions on an Argand diagram. Let their positions be denoted by placed in order in an anticlockwise direction round the circle, starting on the positive -axis. Show the positions of and .
-
EXM.3.AHL.TZ0.2e:
Show that the length of the line segment is .
-
EXM.3.AHL.TZ0.2f:
Hence, write down the total length of the perimeter of the regular sided polygon .
-
EXM.3.AHL.TZ0.2g:
Using part (b) find the limit of this perimeter as .
-
EXM.3.AHL.TZ0.2h:
Find the total area of this sided polygon.
-
EXM.3.AHL.TZ0.2i:
Using part (b) find the limit of this area as .
-
18N.1.AHL.TZ0.H_11a:
Find the roots of which satisfy the condition , expressing your answers in the form , where , .
-
18N.1.AHL.TZ0.H_11b.i:
Show that Re S = Im S.
-
18N.1.AHL.TZ0.H_11b.ii:
By writing as , find the value of cos in the form , where , and are integers to be determined.
-
18N.1.AHL.TZ0.H_11b.iii:
Hence, or otherwise, show that S = .
-
18M.1.AHL.TZ1.H_11a.i:
Express w2 and w3 in modulus-argument form.
-
18M.1.AHL.TZ1.H_11a.ii:
Sketch on an Argand diagram the points represented by w0 , w1 , w2 and w3.
-
18M.1.AHL.TZ1.H_11b:
Show that the area of the quadrilateral Q is .
-
18M.1.AHL.TZ1.H_11c:
Let . The points represented on an Argand diagram by form the vertices of a polygon .
Show that the area of the polygon can be expressed in the form , where .
-
17M.1.AHL.TZ1.H_2a.i:
By expressing and in modulus-argument form write down the modulus of ;
-
17M.1.AHL.TZ1.H_2a.ii:
By expressing and in modulus-argument form write down the argument of .
-
17M.1.AHL.TZ1.H_2b:
Find the smallest positive integer value of , such that is a real number.
-
18M.2.AHL.TZ2.H_1a:
Express in the form , where .
-
18M.2.AHL.TZ2.H_1b:
Find the exact value of the modulus of .
-
18M.2.AHL.TZ2.H_1c:
Find the argument of , giving your answer to 4 decimal places.
-
19M.2.AHL.TZ2.H_8a:
Find the roots of the equation , . Give your answers in Cartesian form.
-
19M.2.AHL.TZ2.H_8b:
One of the roots satisfies the condition .
Given that , express in the form , where , .
-
19M.2.AHL.TZ1.H_6a:
Show the points represented by and on the following Argand diagram.
-
19M.2.AHL.TZ1.H_6b.i:
Find an expression in terms of θ for .
-
19M.2.AHL.TZ1.H_6b.ii:
Find an expression in terms of θ for .
-
19M.2.AHL.TZ1.H_6c:
Hence or otherwise find the value of θ for which .
-
17M.1.AHL.TZ2.H_11a:
Solve .
-
17M.1.AHL.TZ2.H_11b:
Show that .
-
17M.1.AHL.TZ2.H_11c.i:
Find the modulus and argument of in terms of . Express each answer in its simplest form.
-
17M.1.AHL.TZ2.H_11c.ii:
Hence find the cube roots of in modulus-argument form.
-
EXN.1.AHL.TZ0.12a:
Use the binomial theorem to expand . Give your answer in the form where and are expressed in terms of and .
-
EXN.3.AHL.TZ0.2a:
Find .
-
EXN.3.AHL.TZ0.2b:
Determine whether is a Gaussian integer.
-
EXN.3.AHL.TZ0.2c:
On an Argand diagram, plot and label all Gaussian integers that have a norm less than .
-
EXN.3.AHL.TZ0.2d:
Given that where , show that .
-
EXN.3.AHL.TZ0.2e:
By expressing the positive integer as a product of two Gaussian integers each of norm , show that is not a Gaussian prime.
-
EXN.3.AHL.TZ0.2f:
Verify that is not a Gaussian prime.
-
EXN.3.AHL.TZ0.2g:
Write down another prime number of the form that is not a Gaussian prime and express it as a product of two Gaussian integers.
-
EXN.3.AHL.TZ0.2h:
Show that .
-
EXN.3.AHL.TZ0.2i:
Hence show that is a Gaussian prime.
-
EXN.3.AHL.TZ0.2j:
Use proof by contradiction to prove that a prime number, , that is not of the form is a Gaussian prime.
-
21M.2.AHL.TZ1.8a:
Find the modulus of .
-
21M.2.AHL.TZ1.8b:
Find the argument of in terms of .
-
21M.2.AHL.TZ1.8c.i:
Find the minimum value of .
-
21M.2.AHL.TZ1.8c.ii:
For the value of found in part (i), find the value of .
-
21M.3.AHL.TZ2.2a.i:
Show that .
-
21M.3.AHL.TZ2.2a.ii:
Hence, deduce that .
-
21M.3.AHL.TZ2.2b:
Show that .
-
21M.3.AHL.TZ2.2c:
By factorizing , or otherwise, deduce that .
-
21M.3.AHL.TZ2.2d:
Show that .
-
21M.3.AHL.TZ2.2e:
Suggest a value for .
-
21M.3.AHL.TZ2.2f.i:
Write down expressions for and in terms of .
-
21M.3.AHL.TZ2.2f.ii:
Hence, write down an expression for in terms of and .
-
21M.3.AHL.TZ2.2g.i:
Express as a product of linear factors over the set .
-
21M.3.AHL.TZ2.2g.ii:
Hence, using the part (g)(i) and part (f) results, or otherwise, prove your suggested result to part (e).
-
21N.1.AHL.TZ0.12a.i:
Verify that is a root of this equation.
-
21N.1.AHL.TZ0.12a.ii:
Find and , expressing these in the form , where and .
-
21N.1.AHL.TZ0.12b:
Plot the points , and on an Argand diagram.
-
21N.1.AHL.TZ0.12c:
Find .
-
21N.1.AHL.TZ0.12d:
By using de Moivre’s theorem, show that is a root of this equation.
-
21N.1.AHL.TZ0.12e:
Determine the value of .
-
21N.3.AHL.TZ0.1a:
Verify that satisfies the differential equation .
-
21N.3.AHL.TZ0.1b:
Show that .
-
21N.3.AHL.TZ0.1c.i:
.
-
21N.3.AHL.TZ0.1c.ii:
.
-
21N.3.AHL.TZ0.1d:
Hence find, and simplify, an expression for .
-
21N.3.AHL.TZ0.1e:
Show that .
-
21N.3.AHL.TZ0.1f:
Sketch the graph of , stating the coordinates of any axis intercepts and the equation of each asymptote.
-
21N.3.AHL.TZ0.1g:
The hyperbola with equation can be rotated to coincide with the curve defined by .
Find the possible values of .
-
22M.1.AHL.TZ2.12a:
Show that where is the complex conjugate of .
-
22M.1.AHL.TZ2.12b:
Given that , show that is a right-angled triangle.
-
22M.1.AHL.TZ2.12c.i:
Express in terms of .
-
22M.1.AHL.TZ2.12c.ii:
Hence show that .
-
22M.1.AHL.TZ2.12d:
Use the result from part (c)(ii) to show that .
-
22M.1.AHL.TZ2.12e:
Consider the equation , where and .
Given that , deduce that only one equilateral triangle can be formed from the point and the roots of this equation.
AHL 1.14—Complex roots of polynomials, conjugate roots, De Moivre’s, powers & roots of complex numbers
-
19M.2.AHL.TZ1.H_11a:
Show that .
-
16N.1.AHL.TZ0.H_12a:
Determine the value of
(i) ;
(ii) .
-
16N.1.AHL.TZ0.H_12b:
Show that .
-
16N.1.AHL.TZ0.H_12c:
Find the values of that satisfy the equation .
-
16N.1.AHL.TZ0.H_12d:
Solve the inequality .
-
17M.1.AHL.TZ1.H_2a.i:
By expressing and in modulus-argument form write down the modulus of ;
-
17M.1.AHL.TZ1.H_2a.ii:
By expressing and in modulus-argument form write down the argument of .
-
17M.1.AHL.TZ1.H_2b:
Find the smallest positive integer value of , such that is a real number.
-
19M.2.AHL.TZ2.H_8a:
Find the roots of the equation , . Give your answers in Cartesian form.
-
19M.2.AHL.TZ2.H_8b:
One of the roots satisfies the condition .
Given that , express in the form , where , .
-
17M.1.AHL.TZ2.H_11a:
Solve .
-
17M.1.AHL.TZ2.H_11b:
Show that .
-
17M.1.AHL.TZ2.H_11c.i:
Find the modulus and argument of in terms of . Express each answer in its simplest form.
-
17M.1.AHL.TZ2.H_11c.ii:
Hence find the cube roots of in modulus-argument form.
-
17N.1.AHL.TZ0.H_8:
Determine the roots of the equation , , giving the answers in the form where .
-
19M.2.AHL.TZ1.H_2a:
where , , .
-
19M.2.AHL.TZ1.H_2b:
where , .
-
19M.2.AHL.TZ2.H_9b:
Sketch the graph of , stating clearly the coordinates of any maximum and minimum points and intersections with axes.
-
18N.1.AHL.TZ0.H_8:
Consider the equation , where , , , and .
Two of the roots of the equation are log26 and and the sum of all the roots is 3 + log23.
Show that 6 + + 12 = 0.
-
19N.1.AHL.TZ0.H_5a:
Solve the equation, giving the solutions in the form , where .
-
19N.2.AHL.TZ0.H_10a:
Find, in terms of , the probability that lies between 1 and 3.
-
19N.2.AHL.TZ0.H_10b:
Sketch the graph of . State the coordinates of the end points and any local maximum or minimum points, giving your answers in terms of .
-
19N.2.AHL.TZ0.H_10c.i:
.
-
19N.2.AHL.TZ0.H_10c.ii:
.
-
19N.2.AHL.TZ0.H_10c.iii:
the median of .
-
19N.2.AHL.TZ0.H_5:
Consider the expansion of , where and .
The coefficient of is four times the coefficient of . Find the value of .
-
19N.2.AHL.TZ0.H_6:
Let , where and .
One of the roots of is . Find the value of .
-
19N.2.AHL.TZ0.H_8a:
the girls do not sit together.
-
19N.2.AHL.TZ0.H_8b:
the girls do not sit on either end.
-
19N.2.AHL.TZ0.H_8c:
the girls do not sit on either end and do not sit together.
-
20N.2.AHL.TZ0.H_4:
Find the term independent of in the expansion of .
-
20N.2.AHL.TZ0.H_7a:
There are more males than females in the group.
-
20N.2.AHL.TZ0.H_7b:
Two of the teachers, Gary and Gerwyn, refuse to go out for a meal together.
-
EXN.1.AHL.TZ0.12b:
Use de Moivre’s theorem and the result from part (a) to show that .
-
EXN.1.AHL.TZ0.12c:
Use the identity from part (b) to show that the quadratic equation has roots and .
-
21M.1.AHL.TZ1.7:
Consider the quartic equation .
Two of the roots of this equation are and , where .
Find the possible values of .
-
21N.1.AHL.TZ0.12a.i:
Verify that is a root of this equation.
-
21N.1.AHL.TZ0.12a.ii:
Find and , expressing these in the form , where and .
-
21N.1.AHL.TZ0.12b:
Plot the points , and on an Argand diagram.
-
21N.1.AHL.TZ0.12c:
Find .
-
21N.1.AHL.TZ0.12d:
By using de Moivre’s theorem, show that is a root of this equation.
-
21N.1.AHL.TZ0.12e:
Determine the value of .
-
22M.3.AHL.TZ1.2a.i:
Given that and are roots of the equation, write down the third root.
-
22M.3.AHL.TZ1.2a.ii:
Verify that the mean of the two complex roots is .
-
22M.3.AHL.TZ2.2d:
Using the result from part (c), show that when , this equation has at least one complex root.
-
22M.3.AHL.TZ2.2e.i:
By varying the value of in the equation , determine the smallest positive integer value of required to show that Noah is incorrect.
-
22M.3.AHL.TZ2.2e.ii:
Explain why the equation will have at least one real root for all values of .
-
22M.3.AHL.TZ2.2g:
Use your result from part (f)(ii) to show that the equation has at least one complex root.
-
22M.3.AHL.TZ2.2h.i:
State what the result in part (f)(ii) tells us when considering this equation .
-
22M.3.AHL.TZ2.2h.iii:
By writing as a product of one linear and one cubic factor, prove that the equation has at least one complex root.
-
22M.1.AHL.TZ2.12a:
Show that where is the complex conjugate of .
-
22M.1.AHL.TZ2.12b:
Given that , show that is a right-angled triangle.
-
22M.1.AHL.TZ2.12c.i:
Express in terms of .
-
22M.1.AHL.TZ2.12c.ii:
Hence show that .
-
22M.1.AHL.TZ2.12d:
Use the result from part (c)(ii) to show that .
-
22M.1.AHL.TZ2.12e:
Consider the equation , where and .
Given that , deduce that only one equilateral triangle can be formed from the point and the roots of this equation.
AHL 1.15—Proof by induction, contradiction, counterexamples
-
16N.1.AHL.TZ0.H_13a:
Find the value of .
-
16N.1.AHL.TZ0.H_13c:
Use the principle of mathematical induction to prove that
where .
-
16N.1.AHL.TZ0.H_13d:
Hence or otherwise solve the equation in the interval .
-
17M.1.AHL.TZ1.H_8:
Use the method of mathematical induction to prove that is divisible by 9 for .
-
17N.1.AHL.TZ0.H_11a:
Determine whether is an odd or even function, justifying your answer.
-
17N.1.AHL.TZ0.H_11b:
By using mathematical induction, prove that
where .
-
17N.1.AHL.TZ0.H_11c:
Hence or otherwise, find an expression for the derivative of with respect to .
-
17N.1.AHL.TZ0.H_11d:
Show that, for , the equation of the tangent to the curve at is .
-
17M.1.AHL.TZ2.H_8:
Prove by mathematical induction that , where .
-
19M.2.AHL.TZ1.H_8a:
Solve the inequality .
-
19M.2.AHL.TZ1.H_8b:
Use mathematical induction to prove that for , .
-
18M.1.AHL.TZ1.H_6:
Use the principle of mathematical induction to prove that
, where .
-
18M.2.AHL.TZ2.H_6:
Use mathematical induction to prove that for where .
-
18N.1.AHL.TZ0.H_6:
Use mathematical induction to prove that , for .
-
19N.1.AHL.TZ0.H_6:
Consider the function , where . The derivative of is denoted by .
Prove, by mathematical induction, that , .
-
20N.2.AHL.TZ0.H_6:
Use mathematical induction to prove that for .
-
EXN.1.AHL.TZ0.9:
It is given that . (Do not prove this identity.)
Using mathematical induction and the above identity, prove that for .
-
EXN.2.AHL.TZ0.8:
Prove by contradiction that is an irrational number.
-
EXN.3.AHL.TZ0.2j:
Use proof by contradiction to prove that a prime number, , that is not of the form is a Gaussian prime.
-
21M.1.AHL.TZ1.12b:
Use mathematical induction to prove that for .
-
21M.1.AHL.TZ2.12d:
Using mathematical induction and the result from part (b), prove that for .
-
21N.1.AHL.TZ0.11a:
Prove by mathematical induction that for .
-
21N.1.AHL.TZ0.11b:
Hence or otherwise, determine the Maclaurin series of in ascending powers of , up to and including the term in .
-
21N.1.AHL.TZ0.11c:
Hence or otherwise, determine the value of .
-
22M.3.AHL.TZ1.1f:
A polygonal number, , can be represented by the series
where .
Use mathematical induction to prove that where .
-
22M.3.AHL.TZ2.2c:
Given that , deduce that and cannot all be real.
-
22M.3.AHL.TZ2.2f.ii:
Hence state a condition in terms of and that would imply has at least one complex root.
-
22M.1.AHL.TZ1.8:
Consider integers and such that is exactly divisible by . Prove by contradiction that and cannot both be odd.
-
22M.1.AHL.TZ2.9:
Prove by contradiction that the equation has no integer roots.
AHL 1.16—Solution of systems of linear equations
-
17N.2.AHL.TZ0.H_1:
Boxes of mixed fruit are on sale at a local supermarket.
Box A contains 2 bananas, 3 kiwifruit and 4 melons, and costs $6.58.
Box B contains 5 bananas, 2 kiwifruit and 8 melons and costs $12.32.
Box C contains 5 bananas and 4 kiwifruit and costs $3.00.
Find the cost of each type of fruit.
-
18N.1.AHL.TZ0.H_4a:
Find the value of for which the system of equations does not have a unique solution.
-
18N.1.AHL.TZ0.H_4b:
Find the solution of the system of equations when .
-
19N.1.AHL.TZ0.H_3:
Three planes have equations:
, where .
Find the set of values of and such that the three planes have no points of intersection.
-
22M.1.AHL.TZ1.11a:
Show that the three planes do not intersect.
-
22M.1.AHL.TZ1.11b.i:
Verify that the point lies on both and .
-
22M.1.AHL.TZ1.11b.ii:
Find a vector equation of , the line of intersection of and .
-
22M.1.AHL.TZ1.11c:
Find the distance between and .
