| Date | November 2019 | Marks available | 7 | Reference code | 19N.1.AHL.TZ0.H_10 |
| Level | Additional Higher Level | Paper | Paper 1 (without calculator) | Time zone | Time zone 0 |
| Command term | Find | Question number | H_10 | Adapted from | N/A |
Question
Consider .
For the graph of ,
Find .
Show that, if , then .
find the coordinates of the -intercept.
show that there are no -intercepts.
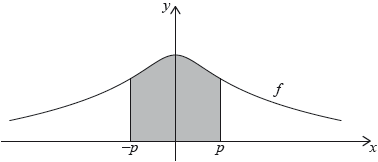
sketch the graph, showing clearly any asymptotic behaviour.
Show that .
The area enclosed by the graph of and the line can be expressed as . Find the value of .
Markscheme
attempt to use quotient rule (or equivalent) (M1)
A1
[2 marks]
simplifying numerator (may be seen in part (i)) (M1)
or equivalent quadratic equation A1
EITHER
use of quadratic formula
A1
OR
use of completing the square
A1
THEN
(since is outside the domain) AG
Note: Do not condone verification that .
Do not award the final A1 as follow through from part (i).
[3 marks]
(0, 4) A1
[1 mark]
A1
outside the domain R1
[2 marks]
A1A1
award A1 for concave up curve over correct domain with one minimum point in the first quadrant
award A1 for approaching asymptotically
[2 marks]
valid attempt to combine fractions (using common denominator) M1
A1
AG
[2 marks]
M1
( or) A1
area under the curve is M1
Note: Ignore absence of, or incorrect limits up to this point.
A1
A1
area is or M1
A1
[7 marks]