| Date | May 2021 | Marks available | 4 | Reference code | 21M.3.AHL.TZ2.2 |
| Level | Additional Higher Level | Paper | Paper 3 | Time zone | Time zone 2 |
| Command term | Show that | Question number | 2 | Adapted from | N/A |
Question
This question asks you to investigate and prove a geometric property involving the roots of the equation where for integers , where .
The roots of the equation where are , where . Each root can be represented by a point , respectively, on an Argand diagram.
For example, the roots of the equation where are and . On an Argand diagram, the root can be represented by a point and the root can be represented by a point .
Consider the case where .
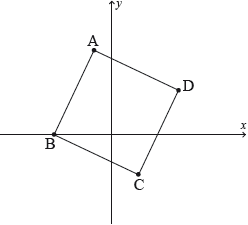
The roots of the equation where are , and . On the following Argand diagram, the points and lie on a circle of radius unit with centre .
Line segments and are added to the Argand diagram in part (a) and are shown on the following Argand diagram.
is the length of and is the length of .
Consider the case where .
The roots of the equation where are and .
On the following Argand diagram, the points and lie on a circle of radius unit with centre . , and are line segments.
For the case where , the equation where has roots and .
It can be shown that .
Now consider the general case for integer values of , where .
The roots of the equation where are . On an Argand diagram, these roots can be represented by the points respectively where are line segments. The roots lie on a circle of radius unit with centre .
can be expressed as .
Consider where .
Show that .
Hence, deduce that .
Show that .
By factorizing , or otherwise, deduce that .
Show that .
Suggest a value for .
Write down expressions for and in terms of .
Hence, write down an expression for in terms of and .
Express as a product of linear factors over the set .
Hence, using the part (g)(i) and part (f) results, or otherwise, prove your suggested result to part (e).
Markscheme
METHOD 1
attempts to expand (M1)
A1
AG
METHOD 2
attempts polynomial division on M1
A1
so AG
Note: In part (a), award marks as appropriate where has been converted into Cartesian, modulus-argument (polar) or Euler form.
[2 marks]
(since is a root of ) R1
and R1
AG
Note: In part (a), award marks as appropriate where has been converted into Cartesian, modulus-argument (polar) or Euler form.
[2 marks]
METHOD 1
attempts to find either or (M1)
accept any valid method
e.g. from either or
e.g. use of Pythagoras’ theorem
e.g. by calculating the distance between points
A1
A1
Note: Award a maximum of M1A1A0 for any decimal approximation seen in the calculation of either or or both.
so AG
METHOD 2
attempts to find (M1)
A1
and since R1
so AG
[3 marks]
METHOD 1
A1
( is a root hence) and R1
AG
Note: Condone the use of throughout.
METHOD 2
considers the sum of roots of (M1)
the sum of roots is zero (there is no term) A1
AG
METHOD 3
substitutes for (M1)
e.g.
A1
Note: This can be demonstrated geometrically or by using vectors. Accept Cartesian or modulus-argument (polar) form.
AG
METHOD 4
A1
as R1
AG
[2 marks]
METHOD 1
A1
attempts to find either or (M1)
Note: For example and .
Various geometric and trigonometric approaches can be used by candidates.
A1A1
Note: Award a maximum of A1M1A1A0 if labels such as are not clearly shown.
Award full marks if the lengths are shown on a clearly labelled diagram.
Award a maximum of A1M1A1A0 for any decimal approximation seen in the calculation of either or or both.
AG
METHOD 2
attempts to find M1
A1
since and A1
and since R1
so AG
METHOD 3
A1
attempts to find M1
A1
since and R1
so AG
[4 marks]
A1
[1 mark]
A1A1
[2 marks]
A1A1
Note: Accept from symmetry.
[1 mark]
considers the equation (M1)
the roots are (A1)
so A1
[3 marks]
METHOD 1
substitutes into M1
(A1)
takes modulus of both sides M1
A1
so AG
Note: Award a maximum of M1A1FTM1A0 from part (e).
METHOD 2
are the roots of M1
coefficient of is and the coefficient of is A1
product of the roots is A1
A1
so AG
[4 marks]