DP Mathematics: Analysis and Approaches Questionbank

AHL 1.12—Complex numbers – Cartesian form and Argand diag
Description
[N/A]Directly related questions
-
20N.1.AHL.TZ0.H_4:
Consider the equation , where and .
Find the value of and the value of .
-
EXN.1.AHL.TZ0.12a:
Use the binomial theorem to expand . Give your answer in the form where and are expressed in terms of and .
-
21M.3.AHL.TZ2.2a.ii:
Hence, deduce that .
-
21M.3.AHL.TZ2.2f.ii:
Hence, write down an expression for in terms of and .
-
21M.2.AHL.TZ2.8:
Consider where .
Show that .
-
21M.3.AHL.TZ2.2a.i:
Show that .
-
21M.3.AHL.TZ2.2d:
Show that .
-
21M.3.AHL.TZ2.2e:
Suggest a value for .
-
21M.3.AHL.TZ2.2g.i:
Express as a product of linear factors over the set .
-
21M.3.AHL.TZ2.2c:
By factorizing , or otherwise, deduce that .
-
21M.3.AHL.TZ2.2f.i:
Write down expressions for and in terms of .
-
21M.3.AHL.TZ2.2b:
Show that .
-
21M.3.AHL.TZ2.2g.ii:
Hence, using the part (g)(i) and part (f) results, or otherwise, prove your suggested result to part (e).
-
21N.1.AHL.TZ0.12c:
Find .
-
21N.1.AHL.TZ0.12b:
Plot the points , and on an Argand diagram.
-
21N.1.AHL.TZ0.12a.ii:
Find and , expressing these in the form , where and .
-
21N.1.AHL.TZ0.12d:
By using de Moivre’s theorem, show that is a root of this equation.
-
21N.1.AHL.TZ0.12e:
Determine the value of .
-
21N.1.AHL.TZ0.12a.i:
Verify that is a root of this equation.
-
21N.3.AHL.TZ0.1b:
Show that .
-
21N.3.AHL.TZ0.1c.i:
.
-
21N.3.AHL.TZ0.1c.ii:
.
-
21N.3.AHL.TZ0.1a:
Verify that satisfies the differential equation .
-
21N.3.AHL.TZ0.1g:
The hyperbola with equation can be rotated to coincide with the curve defined by .
Find the possible values of .
-
21N.3.AHL.TZ0.1e:
Show that .
-
21N.3.AHL.TZ0.1d:
Hence find, and simplify, an expression for .
-
21N.3.AHL.TZ0.1f:
Sketch the graph of , stating the coordinates of any axis intercepts and the equation of each asymptote.
-
22M.3.AHL.TZ1.2e:
Deduce from part (d)(i) that the complex roots of the equation can be expressed as .
-
22M.3.AHL.TZ1.2f.ii:
State the coordinates of .
-
22M.3.AHL.TZ1.2f.i:
Use this diagram to determine the roots of the corresponding equation of the form for .
-
22M.1.AHL.TZ1.9a:
Find an expression for in terms of .
-
22M.1.AHL.TZ2.12e:
Consider the equation , where and .
Given that , deduce that only one equilateral triangle can be formed from the point and the roots of this equation.
-
22M.1.AHL.TZ2.12b:
Given that , show that is a right-angled triangle.
-
22M.1.AHL.TZ2.12d:
Use the result from part (c)(ii) to show that .
-
22M.1.AHL.TZ2.12a:
Show that where is the complex conjugate of .
-
22M.1.AHL.TZ2.12c.i:
Express in terms of .
-
22M.1.AHL.TZ2.12c.ii:
Hence show that .
-
SPM.2.AHL.TZ0.8:
The complex numbers and satisfy the equations
.
Find and in the form where , .
-
16N.1.AHL.TZ0.H_12a:
Determine the value of
(i) ;
(ii) .
-
16N.1.AHL.TZ0.H_12b:
Show that .
-
16N.1.AHL.TZ0.H_12c:
Find the values of that satisfy the equation .
-
16N.1.AHL.TZ0.H_12d:
Solve the inequality .
-
19N.1.AHL.TZ0.H_5b:
The solutions form the vertices of a polygon in the complex plane. Find the area of the polygon.
-
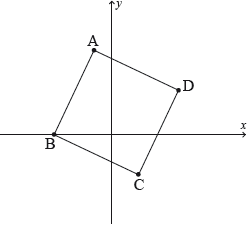
17M.1.AHL.TZ2.H_5:
In the following Argand diagram the point A represents the complex number and the point B represents the complex number . The shape of ABCD is a square. Determine the complex numbers represented by the points C and D.