IB Questionbank

User interface language: English | Español

Date	November 2019	Marks available	5	Reference code	19N.2.AHL.TZ0.H_1
Level	Additional Higher Level	Paper	Paper 2	Time zone	Time zone 0
Command term	Find	Question number	H_1	Adapted from	N/A

Question

A geometric sequence has ${u_4} = - 70$ and ${u_7} = 8.75$ . Find the second term of the sequence.

Markscheme

${u_1}{r^3} = - 70$ , ${u_1}{r^6} = 8.75$ (M1)

${r^3} = \frac{{8.75}}{{ - 70}} = - 0.125$ (A1)

$\Rightarrow r = - 0.5$ (A1)

valid attempt to find ${u_2}$ (M1)

for example: ${u_1} = \frac{{ - 70}}{{ - 0.125}} = 560$

${u_2} = 560 \times - 0.5$

$= - 280$ A1

[5 marks]

Examiners report

[N/A]

Syllabus sections

Topic 1—Number and algebra » SL 1.3—Geometric sequences and series

Show 68 related questions

19M.2.AHL.TZ1.H_11b:
Show that one of the real roots is equal to 1.
19M.2.SL.TZ1.T_5a:
Calculate, in CAD, the total amount John pays for the bicycle.
17M.1.SL.TZ1.S_7a:
Find the common ratio.
17M.1.SL.TZ2.T_9a:
Write down the common ratio of the sequence.
17N.1.SL.TZ0.S_10b:
The following diagram shows [CD], with length $b{\text{ cm}}$ , where $b > 1$ . Squares with side lengths $k{\text{ cm}},{\text{ }}{k^2}{\text{ cm}},{\text{ }}{k^3}{\text{ cm}},{\text{ }} \ldots$ , where $0 < k < 1$ , are drawn along [CD]. This process is carried on indefinitely. The diagram shows the first three squares.

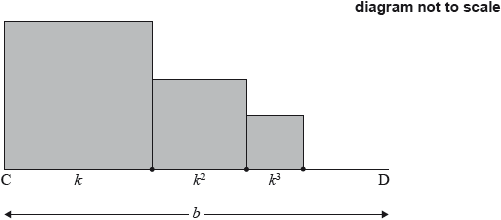
The total sum of the areas of all the squares is $\frac{9}{{16}}$ . Find the value of $b$ .
19M.2.AHL.TZ1.H_11a:
Show that $abc = 8$ .
18M.2.SL.TZ2.S_4b:
Find the sum of the first 8 terms.
18M.1.SL.TZ1.S_10c:
Find the values of θ which give the greatest value of the sum.
22M.1.SL.TZ1.8a.ii:
Given that $p > 0$ and $S_{\infty} = 3 + \sqrt{3}$ , find the value of $x$ .
22M.1.AHL.TZ1.10a.ii:
Hence or otherwise, show that the series is convergent.
22M.1.AHL.TZ1.10a.iii:
Given that $p > 0$ and $S_{\infty} = 3 + \sqrt{3}$ , find the value of $x$ .
20N.2.AHL.TZ0.H_11e.i:
Show that, at these times, $\tan 6 t = 2$ .
EXN.2.SL.TZ0.7c.i:
Find the value of $N$ .
EXN.2.SL.TZ0.7b:
Given that $J_{n}$ follows a geometric sequence, state the value of the common ratio, $r$ .
EXN.2.SL.TZ0.7d:
Find Jane’s total earnings at the start of her $10$ th year of employment. Give your answer correct to the nearest dollar.
20N.2.AHL.TZ0.H_11c:
Find the maximum displacement of $P$ , in metres, from its initial position.
18M.1.SL.TZ1.S_10a.i:
Find an expression for r in terms of θ.
18M.2.SL.TZ2.S_4a:
Find the common ratio.
16N.1.AHL.TZ0.H_10a:
Show that ${\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(A' \cap B)$ .
19N.2.SL.TZ0.S_5c:
Find the least value of $n$ such that ${S_n} > 5543$ .
21M.2.SL.TZ2.9c:
Given that the grand prize is not won and the grand prize continues to double, write an expression in terms of $n$ for the value of the grand prize in the $n th$ week of the lottery.
20N.2.AHL.TZ0.H_11b:
Find an expression for $s$ in terms of $t$ .
17M.1.SL.TZ1.T_10a:
Find the value of $r$ , the common ratio of the sequence.
20N.1.AHL.TZ0.H_5:
The first term in an arithmetic sequence is $4$ and the fifth term is $\log_{2} 625$ .

Find the common difference of the sequence, expressing your answer in the form $\log_{2} p$ , where $p \in ℚ$ .
EXN.2.SL.TZ0.7a:
Show that $H_{n} = 2400 n + 67 600$ .
18N.2.AHL.TZ0.H_1b:
Find the sum to infinity of this sequence.
19M.2.AHL.TZ1.H_11c:
Given that $q = 8{d^2}$ , find the other two real roots.
EXN.2.SL.TZ0.7c.ii:
For the value of $N$ found in part (c) (i), state Helen’s annual salary and Jane’s annual salary, correct to the nearest dollar.
22M.1.AHL.TZ1.10a.i:
Show that $p = \pm \frac{1}{\sqrt{3}}$ .
22M.1.SL.TZ1.8a.i:
Show that $p = \pm \frac{1}{\sqrt{3}}$ .
21N.1.SL.TZ0.8b:
Write down an expression for $f^{- 1} (x)$ .
22M.2.SL.TZ2.3a:
Find Gemma’s annual salary for the year 2021, to the nearest dollar.
17M.1.SL.TZ2.T_9c:
Find the smallest value of $n$ for which ${u_n}$ is less than ${10^{ - 3}}$ .
17N.2.SL.TZ0.T_2b:
Find the value of $k$ .
16N.1.SL.TZ0.T_10c:
Find the total depth that the post has been driven into the ground after 10 strikes of the hammer.
18M.2.SL.TZ2.T_4b:
Calculate the café’s total profit for the first 12 weeks.
21N.2.SL.TZ0.6a:
Find the first term of the sequence, $u_{1}$ .
21N.2.SL.TZ0.6b:
Find $S_{\infty}$ .
19N.2.SL.TZ0.S_5b:
Find the value of ${u_{10}}$ .
21N.1.SL.TZ0.8c:
Find the value of $f^{- 1} (\sqrt{32})$ .
18M.2.SL.TZ2.S_4c:
Find the least value of n for which S_n > 163.
17M.2.SL.TZ2.S_5:
Consider a geometric sequence where the first term is 768 and the second term is 576.

Find the least value of $n$ such that the $n$ th term of the sequence is less than 7.
20N.2.AHL.TZ0.H_11a:
Find the times when $P$ comes to instantaneous rest.
19N.2.SL.TZ0.S_5a:
Find the value of $r$ .
20N.2.AHL.TZ0.H_11e.ii:
Hence show that $\frac{v_{2}}{v_{1}} = \frac{v_{3}}{v_{2}} = - e^{- \frac{π}{2}}$ .
20N.2.AHL.TZ0.H_11d:
Find the total distance travelled by $P$ in the first $1.5$ seconds of its motion.
20N.1.SL.TZ0.T_15a:
Find the common ratio of the sequence.
20N.1.SL.TZ0.T_15b:
Find the volume of the smallest slice of pie.
16N.1.SL.TZ0.T_10b:
Find the distance that the post is driven into the ground by the eighth strike of the hammer.
17N.2.SL.TZ0.T_2e:
Calculate the total distance Carlos runs in the first year.
17M.1.SL.TZ2.T_9b:
Find the value of ${u_5}$ .
20N.1.SL.TZ0.T_15c:
The apple pie has a volume of $61 425 {cm}^{3}$ .

Find the total number of slices Mia can cut from this pie.
17M.1.SL.TZ1.T_10c:
Find the sum of the first 30 terms of the sequence.
16N.1.SL.TZ0.T_10a:
Find the value of the common ratio for this sequence.
19M.2.SL.TZ1.T_5e:
John purchased the bicycle in 2008.

Justify why John should not insure his bicycle in 2019.
17M.1.SL.TZ1.T_10b:
Find the value of $n$ for which ${u_n} = 2$ .
21N.1.SL.TZ0.8a:
Show that $a = 8$ .
21N.1.SL.TZ0.8d.ii:
Find the value of $p$ and the value of $q$ .
21N.1.SL.TZ0.8d.i:
Show that $27, p, q$ and $125$ are four consecutive terms in a geometric sequence.
21N.2.SL.TZ0.6c:
Find the least value of $n$ such that $S_{\infty} - S_{n} < 0.001$ .
19M.2.SL.TZ1.T_5b:
Find the value of the bicycle during the 5th year. Give your answer to two decimal places.
19M.2.SL.TZ1.T_5c:
Calculate, in years, when the bicycle value will be less than 50 USD.
19M.2.SL.TZ1.T_5d:
Find the total amount John has paid to insure his bicycle for the first 5 years.
17N.2.SL.TZ0.T_2a.i:
Write down the distance Rosa runs in the third training session;
17N.2.SL.TZ0.T_2a.ii:
Write down the distance Rosa runs in the $n$ th training session.
17N.2.SL.TZ0.T_2c:
Calculate the total distance, in kilometres, Rosa runs in the first 50 training sessions.
17N.2.SL.TZ0.T_2d:
Find the distance Carlos runs in the fifth month of training.
18M.2.SL.TZ2.T_4d:
Calculate the tea-shop’s total profit for the first 12 weeks.

Hide related questions

Topic 1—Number and algebra

Question

Markscheme

Examiners report

Syllabus sections

View options