Manipulating equilibrium constants

The importance of the relationship between the equilibrium constant and the balanced stoichiometric equilibrium reaction it relates to is stressed. What happens to the value of the equilibrium constant when the coefficients of the reactants and products are altered, the reaction is reversed or when reactions are combined  is covered with examples. Finally a worked example demonstrate why the ability to manipulate known equilibrium constants is a useful tool for finding the value of an unknown equilibrium constant.

Introduction

Students often have difficulty with manipulating equilibrium constants. One of the reasons may be a lack of understanding as to what equilibrium actually represents.

 A state of chemical equilibrium is reached in a closed system when the rate of the forward reaction is equal to the rate of the reverse reaction. That is for the reaction:

wA  +  xB   ⇌     yC + zD

the rate at which A and B are reacting to form C and D is equal to the rate that C and D are reacting to form A and B. Unlike the image of static equilibrium above that I made from stones and driftwood on my local beach, chemical equilibrium is dynamic, i.e. when the position of equilibrium has been reached, the forward and reverse reactions are still occurring but there is no change in the concentrations of reactants and products. The IB is only concerned with homogenous equlibria, i.e. the reactants and products are all in the same phase and also the IB only requires equilibrium constants to be expressed in concentrations (rather than in terms of partial pressures).

For the above reaction the equilibrium law states

Kc = 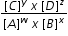 begin mathsize 12px style fraction numerator left square bracket C right square bracket to the power of y space x space left square bracket D right square bracket to the power of z over denominator left square bracket A right square bracket to the power of w space x space left square bracket B right square bracket to the power of x end fraction end style  where Kc is known as the equilibrium constant at a stated temperature.

Although expressed in terms of concentrations, equilibrium constants have no units as technically the square brackets represent activities rather than concentrations and activities have no units. If the system is not in equilibrium then the reaction quotient, Q can be used. The reaction quotient measures the relative amount of products and reactants present during a reaction at a particular point in time by using the non-equilibrium concentrations in the equilibrium expression.

The definition of the equilibrium expression and the way in which it relates to a stated stoichiometric equation is important and underlies how equilibrium constants can be manipulated.

  The relationship between different equilibrium constants for the same reaction (at the same temperature) when represented by equations written in different ways.

1. Changing the coefficients

Consider the equilibrium reaction between gaseous hydrogen and gaseous iodine to from gaseous hydrogen iodide.

H2(g) + I2(g) ⇌ 2HI(g)

By definition the equilibrium constant Kc for this reaction is defined by the equation

Kc = fraction numerator text [HI(g)] end text to the power of text 2 end text end exponent over denominator text [H end text subscript text 2 end text end subscript text (g)] x [I end text subscript text 2 end text end subscript text (g)] end text end fraction

If we had written the equation as ½H2(g) + ½I2(g) ⇌ HI(g) it is still the same reaction but now the new equilibrium constant, Kc’ is given by the expression

Kc' =  fraction numerator text [HI(g)] end text over denominator text [H end text subscript text 2 end text end subscript text (g) end text right square bracket to the power of text 1/2 end text end exponent space x space text [I end text subscript text 2 end text end subscript text (g)] end text to the power of text 1/2 end text end exponent end fraction

Hence Kc' = √Kc

2. Reversing the direction of the reaction

If we look at the reverse reaction

2HI(g) ⇌ H2(g) + I2(g)

The equilibrium constant Kc” for this reverse reaction  is given by the expression

Kc” = fraction numerator text [H end text subscript text 2 end text end subscript text (g)] x [I end text subscript text 2 end text end subscript text (g)]  end text over denominator text [HI(g)] end text to the power of text 2 end text end exponent end fraction

Hence  Kc” = 1/Kc.

3. Combining chemical reactions

A third relationship is when two (or more) equations can be combined to give a new equation. The equilibrium constant for the new reaction is equal to the product of the equilibrium constants for the two (or more) reactions that are being combined, i.e. for the combination of three equations Kc = Kc1 x Kc2 x Kc3.

For example if we use the equations given above for the reaction between hydrogen and iodine then if we take ½H2(g) + ½I2(g) ⇌ HI(g) for which Kc’ = √Kc and add it to another ½H2(g) + ½I2(g) ⇌ HI(g) we arrive back at the original equation of H2(g) + I2(g) ⇌ 2HI(g). The equilibrium constant for this reaction = Kc’ x Kc’ = √Kc x √Kc = Kc.

All three of these ways of manipulating equilibrium constants according to the stated reaction are covered in Topic 7 Equilibrium.

Worked example

The ability to utilise and manipulate equilibrium constants in this way can be useful to determine the value of an unknown equilibrium constant for a reaction from the values of the equilibrium constants for known reactions. For example:

(a) The equilibrium constants for the following three reactions are given as Kc1, Kc2 and Kc3 respectively.

(1)  2N2O(g)  ⇌  2N2 (g) + O2(g)        Kc1


(2)  2NO2(g) ⇌ N2O4(g)                      Kc2


(3)  N2(g) + 2O2(g) ⇌  2NO2(g)           Kc3

Derive the expression for the equilibrium constant, Kc for the reaction

2N2O(g) + 3O2(g) ⇌ 2N2O4(g)

in terms of Kc1, Kc2 and Kc3.

Worked answer

Double equations (2) and (3) and add then to equation (1)

2N2O(g)  ⇌  2N2 (g) + O2(g)        Kc1

4NO2(g) ⇌ 2N2O4(g)                    Kc’ = (Kc2)2

2N2(g) + 4O2(g) ⇌  4NO2(g)        Kc” =  (Kc3)2

-------------------------------------

2N2O(g) + 3O2(g) ⇌ 2N2O4(g)     Kc = Kc1 x (Kc2)2 x (Kc3)2

(b) Using the following data calculate the value for the equilibrium constant at 298 K for the reaction

2N2O(g) + 3O2(g) ⇌ 2N2O4(g)

Worked answer

The 1st reaction is equation (1) reversed so Kc1 = 1/1.2 x 10−35 = 8.33 x 1034

The 2nd reaction is equation (2) reversed so Kc2 = 1/(4.6 x 10−3) and (Kc2)2 = (1/4.6 x 10−3)2 = 4.73 x 104

The 3rd reaction needs to be multiplied by 2 to give equation (3) so Kc3 = (4.1 x 10−9)2 and (Kc3)2 = (4.1 x 10−9)4 = 2.83 x 10−34   

Hence Kc for 2N2O(g) + 3O2(g)  ⇌ 2N2O4(g)

= Kc1 x (Kc2)2 x (Kc3)2 = 8.33 x 1034  x  4.73 x 104  x 2.83 x 10−34 = 1.1 x 106      

All materials on this website are for the exclusive use of teachers and students at subscribing schools for the period of their subscription. Any unauthorised copying or posting of materials on other websites is an infringement of our copyright and could result in your account being blocked and legal action being taken against you.