4.3.2 Amplitude & Intensity

Power per unit area

The rate of energy transfer

The rate of energy transfer per unit area

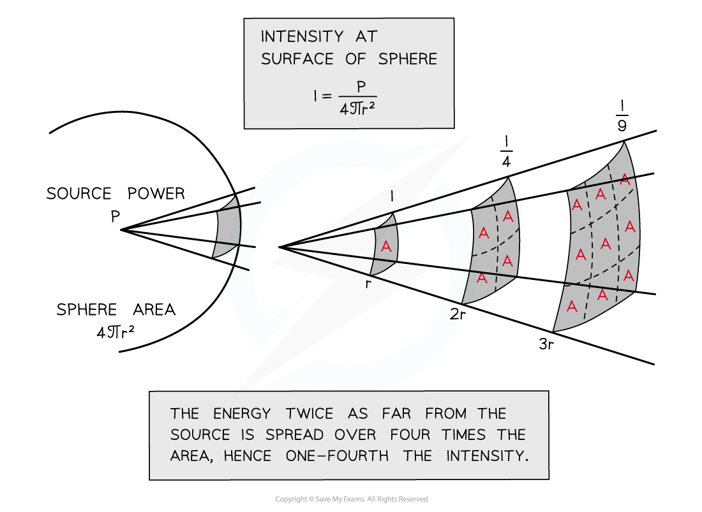
For spherical waves being emitted by a point source equally in all directions, the intensity follows an inverse square law with distance from the point source

$I \propto \frac{1}{r^{2}}$

Where:
- I = intensity of the wave in watts per metre squared (W m^–2)
- r = distance from the point source in metres (m)

For spherical waves being emitted by a point source equally in all directions, the intensity at the surface of a sphere is calculated using:

I = $\frac{P}{4 π r^{2}}$

Where:
- P = power in watts (W)
- r = radius of sphere in metres (m)
For spherical waves being emitted by a point source equally in all directions, the power is a constant, therefore the relationship can be expressed as:

I ∝ $\frac{1}{r^{2}}$

I ∝ x⁻²

7117-intensity-of-a-spherical-wave

Intensity decreases by the inverse square law

By definition, the intensity of a wave (its power per unit area) is proportional to the energy transferred by the wave
The intensity of a wave at a particular point is related to the amplitude of the wave at that point
The energy transferred by a wave is proportional to the square of the amplitude
Therefore, the intensity of a wave is proportional to the square of the amplitude

$I \propto A^{2}$

Where:
- I = intensity of the wave in W m^–2
- A = amplitude of the wave in metres (m)

A person stands 10 m away from a loudspeaker. The sound produced by the loudspeaker is very loud, so the person moves 20 m away from it.

State the effect of this change on the intensity and the amplitude of the sound waves heard by the person.

Step 1: Write down the known quantities

Step 2: Write down the relationship between the intensity of a wave and the distance from the point source producing the wave

Step 2: State the new intensity

- Since the distance doubles (r₂ = 2r₁), the intensity is reduced by a factor four

Step 3: Write down the relationship between the intensity of a wave and its amplitude

Step 4: State the new amplitude

- Since the intensity is reduced by a factor four, the amplitude decreases by half

DP IB Physics: HL

4.3.2 Amplitude & Intensity