10.1.1 Gravitational & Electrostatic Fields

• A field can be defined as

A region in which an object will experience a force, such as gravitational or electrostatic, at a distance

• A gravitational field can be defined as:

The gravitational force per unit mass exerted on a point mass

• An electrostatic field can be defined as:

The electric force per unit charge exerted on a small positive test charge

• Fields can be described in terms of field strength, which is defined as:

• Electric field strength, E, and gravitational field strength, g, therefore, have very similar equations
  • Despite a few differences, they are analogous to one another in many ways
• In both cases, the nature of the test object is as follows:
  • Gravitational fields: small mass, m
  • Electrostatic fields: small positive charge, q

 

Uniform Fields

• A gravitational field is a region of space in which objects with mass will experience a force
• The gravitational field strength can be calculated using the equation:

• Where:
  • g = gravitational field strength (N kg^-1)
  • F = gravitational force on the mass (N)
  • m = mass (kg)

• The direction of the gravitational field is always directed towards the centre of the mass
  • Gravitational forces are always attractive and cannot be repulsive

---

• An electric field is a region of space in which an electric charge will experience a force
• The electric field strength can be calculated using the equation:

• Where:
  • E = electric field strength (N C^-1)
  • F = electrostatic force on the charge (N)
  • Q = Charge (C)
• It is important to use a positive test charge in this definition, as this determines the direction of the electric field
• The electric field strength is a vector quantity, it is always directed:
  • Away from a positive charge
  • Towards a negative charge
• Opposite charges (positive and negative) attract each other
• Conversely, like charges (positive-positive or negative-negative) repel each other

• The magnitude of the electric field strength in a uniform field between two charged parallel plates is defined as:

• Where:
  • E = electric field strength (V m^-1)
  • V = potential difference between the plates (V)
  • d = separation between the plates (m)

 

• The electric field strength is now defined by the units V m^–1 
  • Therefore, the units V m^–1 are equivalent to the units N C^–1

• The equation shows:
  • The greater the voltage (potential difference) between the plates, the stronger the field
  • The greater the separation between the plates, the weaker the field

   

• This equation cannot be used to find the electric field strength around a point charge (since this would be a radial field)
• The direction of the electric field is from the plate connected to the positive terminal of the cell to the plate connected to the negative terminal

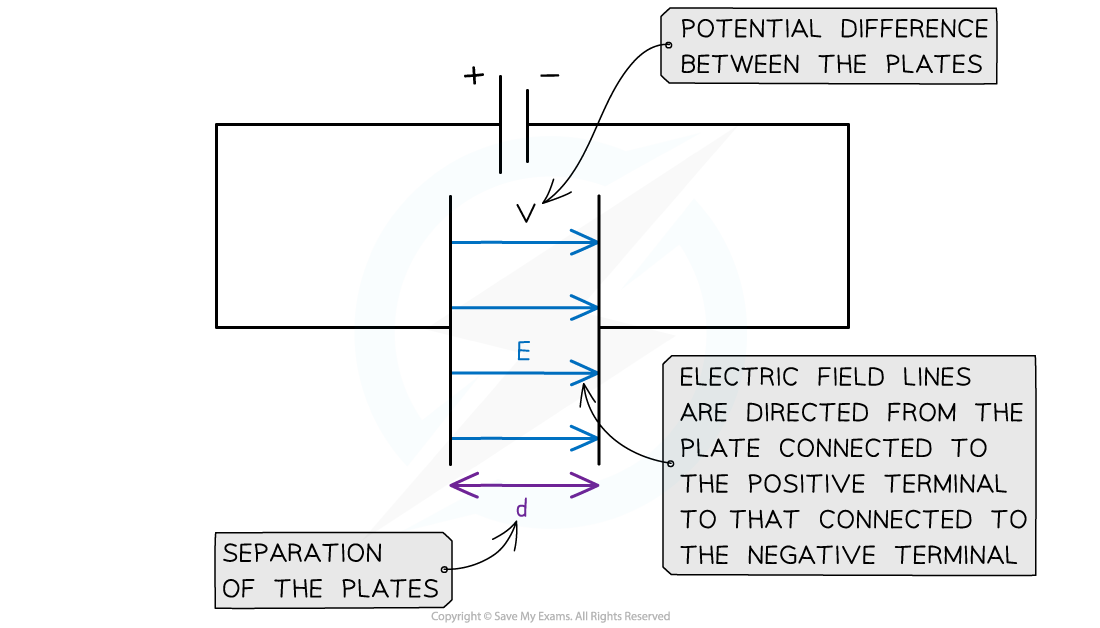
The E field strength between two charged parallel plates is the ratio of the potential difference and separation of the plates

• Note: if one of the parallel plates is earthed, it has a voltage of 0 V

Radial Fields

• A point charge or mass produces a radial field
  • A charged sphere also acts as a point charge
  • A spherical mass also acts as a point mass

• Radial fields always have an inverse square law relationship with distance
  • This means the field strength decreases by a factor of four when the distance r is doubled

• The gravitational force F_G between two masses is defined by:

• Where:
• F_G = gravitational force between two masses (N)
• G = Newton’s gravitational constant
• m₁, m₂ = two points masses (kg)
• r = distance between the centre of the two masses (m)

---

• The electric field strength E at a distance r due to a point charge Q in free space is defined by:

• Where:
• Q = the point charge producing the radial electric field (C)
• r = distance from the centre of the charge (m)
• ε₀ = permittivity of free space (F m^-1) = ()

• This equation shows:
  • The electric field strength in a radial field is not constant
  • As the distance, r, from the charge increases, E decreases by a factor of 1/r²

Gravitational vs Electrostatic Forces

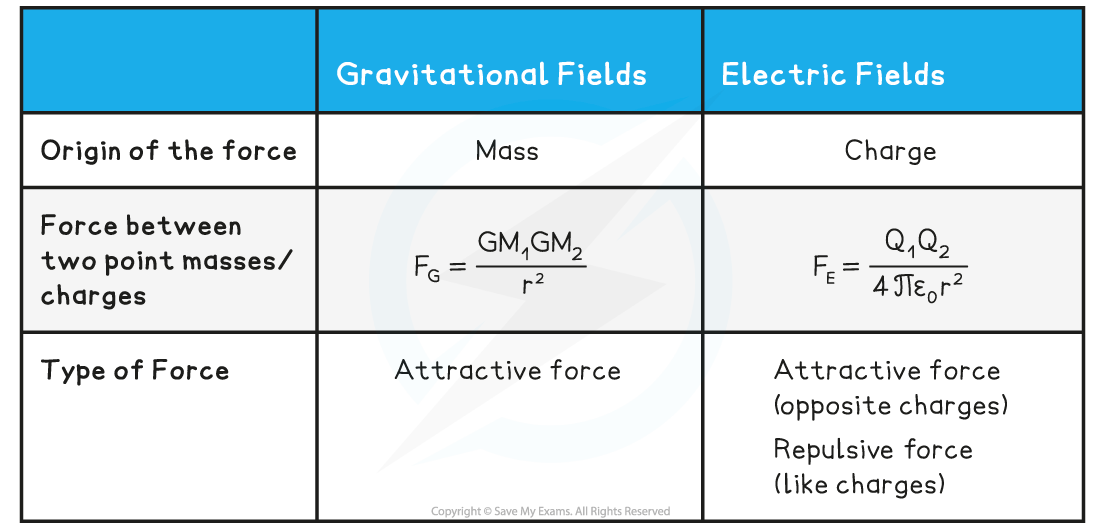
• The similarities and differences between gravitational and electrostatic forces are listed in the table below:

Comparing G and E Fields 

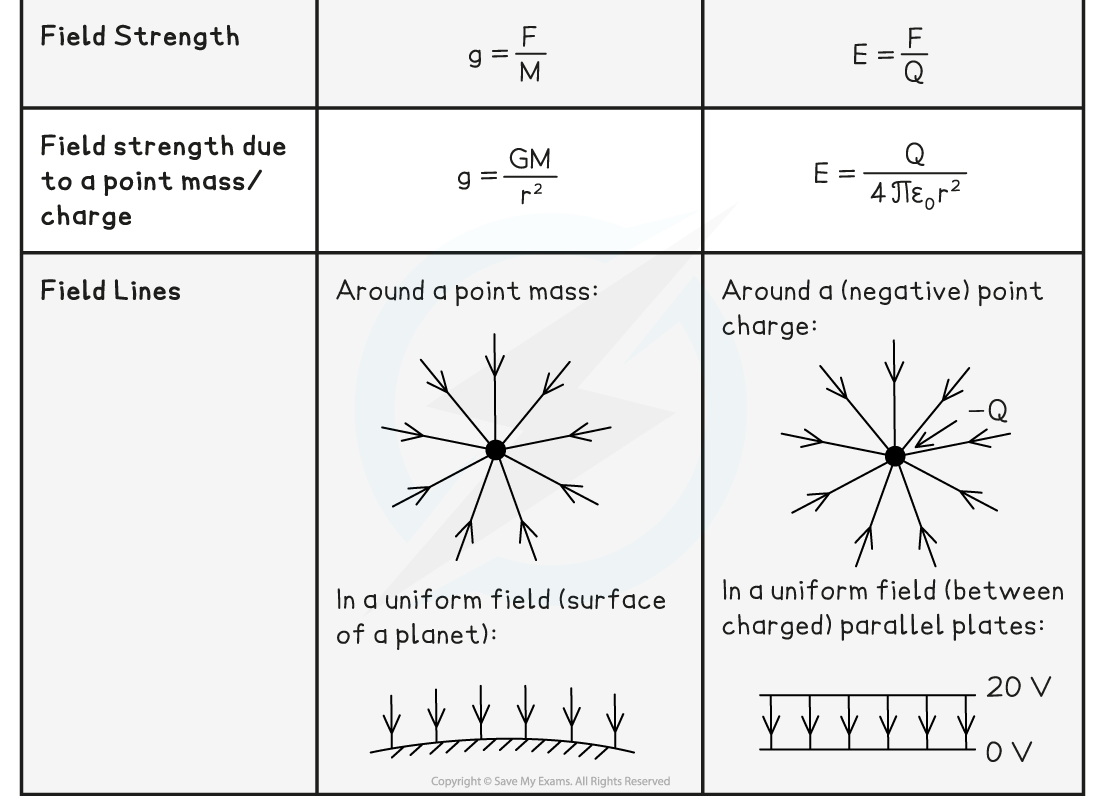
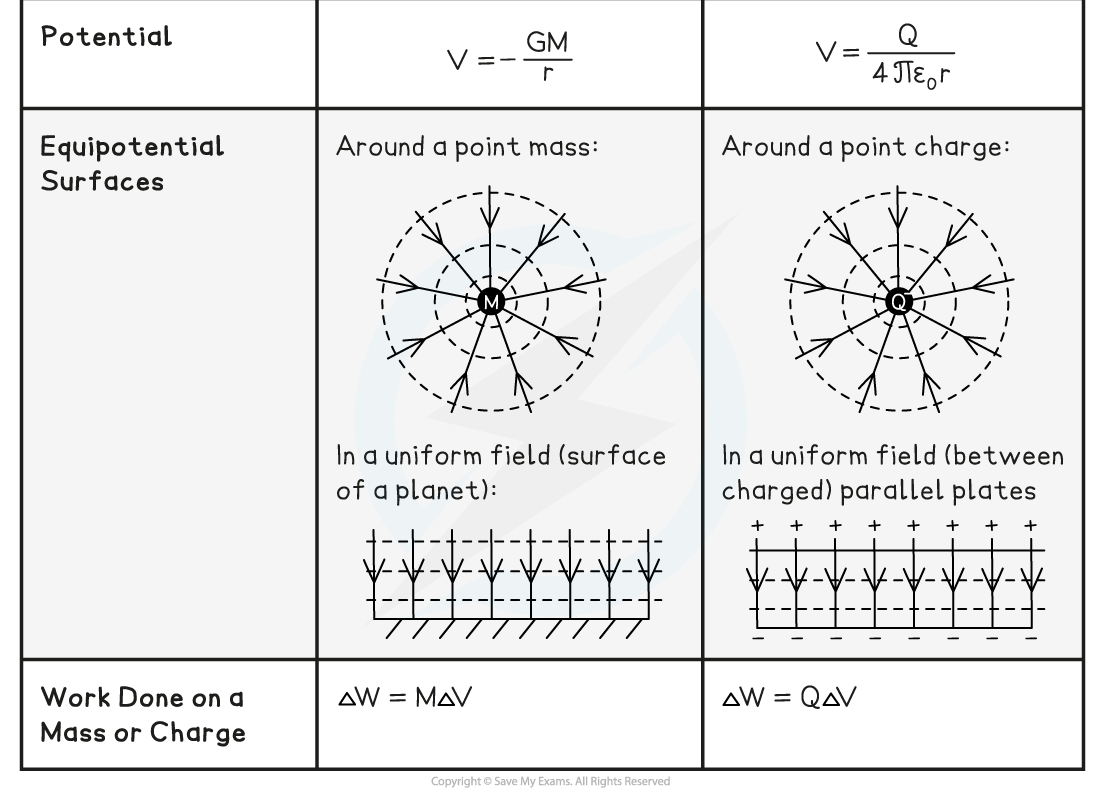
• The key similarities are:
  • The magnitude of the gravitational and electrostatic force between two point masses or charges are inverse square law relationships
  • The field lines around a point mass and negative point charge are identical
  • The field lines in a uniform gravitational and electric field are identical
  • The gravitational field strength and electric field strength both have a 1 / r² relationship in a radial field
  • The gravitational potential and electric potential both have a 1 / r relationship
  • Equipotential surfaces for both gravitational and electric fields are spherical around a point mass or charge and equally spaced parallel lines in uniform fields
  • The work done in each field is either the product of the mass and change in potential or charge and change in potential

• The key differences are:
  • The gravitational force acts on particles with mass whilst the electrostatic force acts on particles with charge
  • The gravitational force is always attractive whilst the electrostatic force can be attractive or repulsive
  • The gravitational potential is always negative whilst the electric potential can be either negative or positive

Worked Example

Step 1: Write down the known values

• • Potential difference, V = 7.9 kV = 7.9 × 10³ V
  • Distance between plates, d = 3.5 cm = 3.5 × 10^-2 m
  • Charge, Q = 2.6 × 10^-15 C

Step 2: Calculate the electric field strength between the parallel plates

Step 3: Write out the equation for electric force on a charged particle

Step 4: Substitute electric field strength and charge into electric force equation

Exam Tip