Properties of Waves
- Travelling waves are defined as follows:
Oscillations that transfer energy from one place to another without transferring matter
- Energy is transferred by the waves, but matter is not
- The direction of the motion of the wave is the direction of the energy transfer
- Travelling waves can be of two types:
- Mechanical Waves, which propagate through a medium and cannot take place in a vacuum
- Electromagnetic Waves, which can travel through a vacuum
- Waves are generated by oscillating sources
- These oscillations travel away from the source
- Oscillations can propagate through a medium (e.g. air, water) or in vacuum (i.e. no particles), depending on the type of wave
- The key properties of travelling waves are as follows:
- Displacement (x) of a wave is the distance of a point on the wave from its equilibrium position
- It is a vector quantity; it can be positive or negative
- Measured in metres (m)
- Wavelength (λ) is the length of one complete oscillation measured from same point on two consecutive waves
- For example, two crests, or two troughs
- Measured in metres (m)
- Amplitude (x0) is the maximum displacement of an oscillating wave from its equilibrium position (x = 0)
- Amplitude can be positive or negative depending on the direction of the displacement
- Measured in metres (m)
- Period (T) is the time taken for a fixed point on the wave to undergo one complete oscillation
- Measured in seconds (s)
- Frequency (f) is the number of full oscillations per second
- Measured in Hertz (Hz)
- Wave speed (c) is the distance travelled by the wave per unit time
- Measured in metres per second (m s-1)
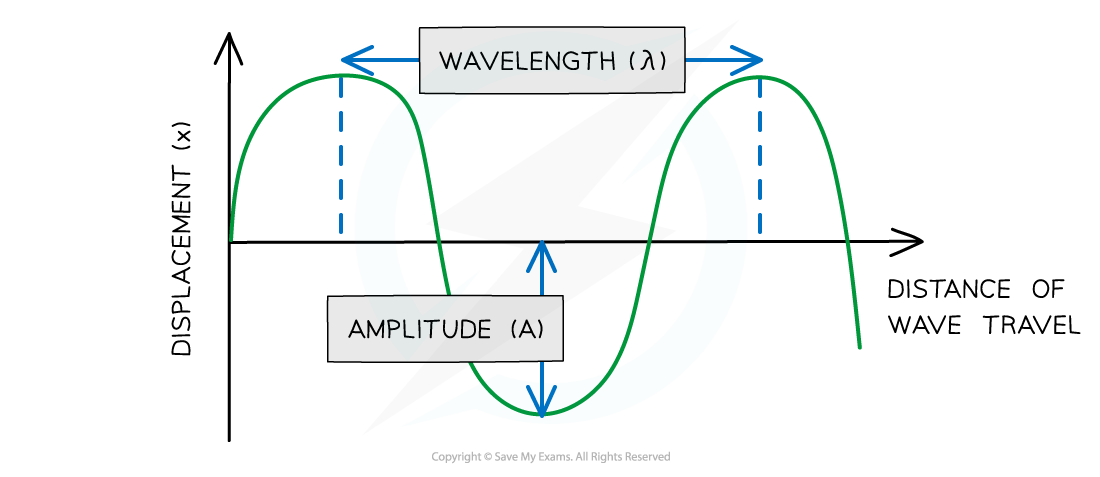
Diagram showing the amplitude and wavelength of a wave
- The frequency, f, and the period, T, of a travelling wave are related to each other by the equation:

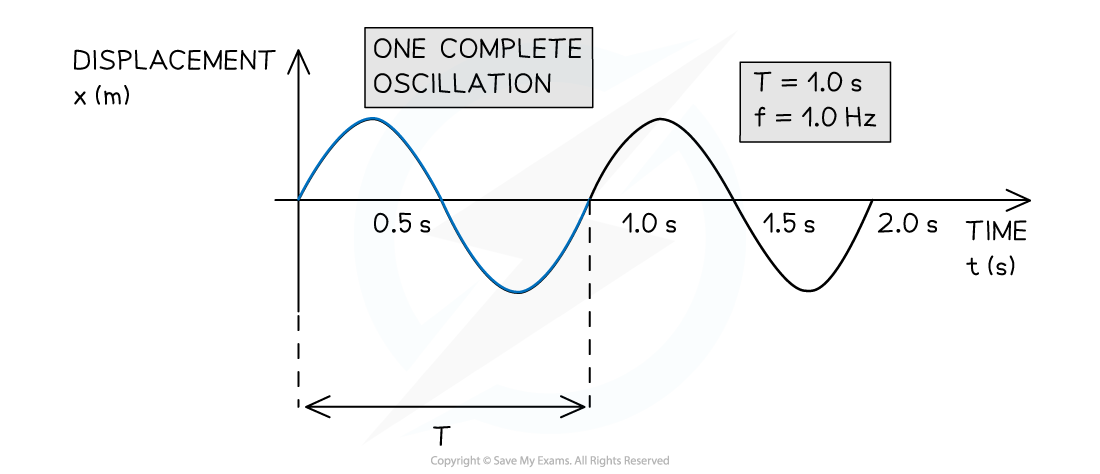
Period T and frequency f of a travelling wave
Worked Example
The graph below shows a travelling wave. Determine:
Determine:
(i) The amplitude A of the wave in metres (m)
(ii) The frequency f of the wave in hertz (Hz)
(i) Identify the amplitude A of the wave on the graph
-
- The amplitude is defined as the maximum displacement from the equilibrium position (x = 0)

-
- The amplitude must be converted from centimetres (cm) into metres (m)
(ii) Calculate the frequency of the wave
Step 1: Identify the period T of the wave on the graph
-
- The period is defined as the time taken for one complete oscillation to occur
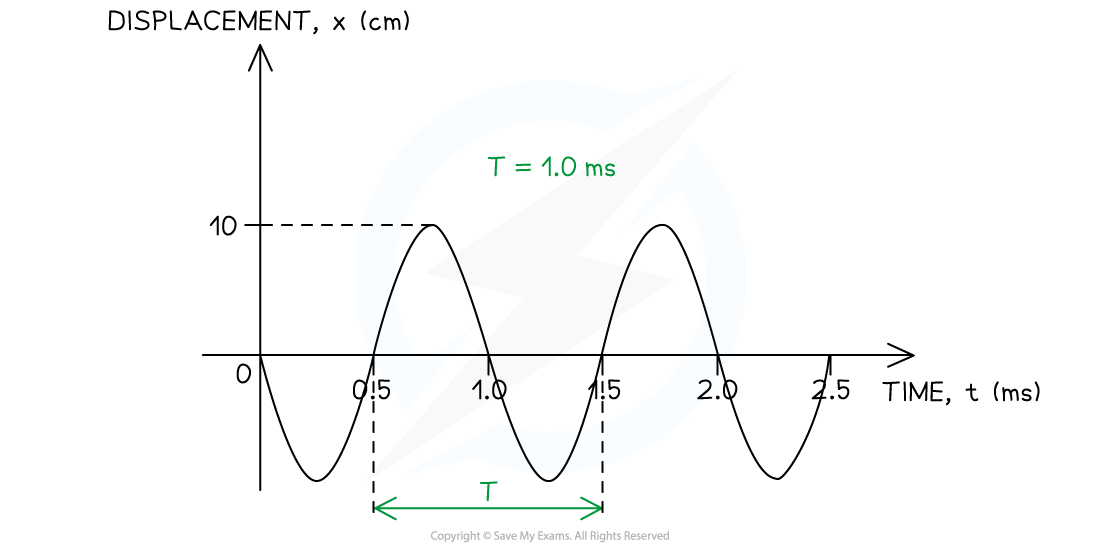
-
- The period must be converted from milliseconds (ms) into seconds (s)
T = 1 × 10–3 s
Step 2: Write down the relationship between the frequency f and the period T
Step 3: Substitute the value of the period determined in Step 1
![]()
f = 1000 Hz
The Wave Equation
- The wave equation describes the relationship between the wave speed, the wavelength and the frequency of the wave
c = fλ
- Where
- c = wave speed in metres per second (m s−1)
- f = frequency in hertz (Hz)
- λ = wavelength in metres (m)
Deriving the Wave Equation
- The wave equation can be derived using the equation for speed
v =
- Where
- v = velocity or speed in metres per second (m s−1)
- d = distance travelled in metres (m)
- t = time taken in seconds (s)
- When the source of a wave undergoes one complete oscillation, the travelling wave propagates forward by a distance equal to one wavelength λ
- The travelling wave covers this distance in the time it takes the source to complete one oscillation, the time period T
wave speed = =
- Therefore, the wave speed c is given by
c =
- The period T of a wave is given by:
T =
- Therefore, combining these equations gives the wave equation
c = fλ
Worked Example
A travelling wave has a period of 1.0 μs and travels at a velocity of 100 cm s–1. Calculate the wavelength of the wave. Give your answer in metres (m).
Step 1: Write down the known quantities
- Period, T = 1.0 μs = 1.0 × 10–6 s
- Velocity, c = 100 cm s–1 = 1.0 m s–1
Note the conversions:
- The period must be converted from microseconds (μs) into seconds (s)
- The velocity must be converted from cm s–1 into m s–1
Step 2: Write down the relationship between the frequency f and the period T
![]()
Step 3: Substitute the value of the period into the above equation to calculate the frequency
![]()
f = 1.0 × 106 Hz
Step 4: Write down the wave equation
c = fλ
Step 5: Rearrange the wave equation to calculate the wavelength λ
![]()
Step 6: Substitute the numbers into the above equation
![]()
λ = 1 × 10–6 m
