11.3.4 The Time Constant

• The time constant of a capacitor discharging through a resistor is a measure of how long it takes for the capacitor to discharge
• The definition of the time constant is:

The time taken for the charge, current or voltage of a discharging capacitor to decrease to 37% of its original value

• Alternatively, for a charging capacitor:

The time taken for the charge or voltage of a charging capacitor to rise to 63% of its maximum value

• 37% is 0.37 or  (where e is the exponential function) multiplied by the original value (I₀, Q₀ or V₀)
  • This is represented by the Greek letter tau, ,  and measured in units of seconds (s)
• The time constant provides an easy way to compare the rate of change of similar quantities eg. charge, current and p.d.
• It is defined by the equation:

 = RC

• Where:
  •  = time constant (s)
  • R = resistance of the resistor (Ω)
  • C = capacitance of the capacitor (F)

The graph of voltage-time for a discharging capacitor showing the positions of the first three time constants

 

• The time to half, t_1/2 (half-life) for a discharging capacitor is:

The time taken for the charge, current or voltage of a discharging capacitor to reach half of its initial value

• This can also be written in terms of the time constant, :

t_1/2 = ln(2) ≈ 0.69  = 0.69 RC

Exam Tip

• Problems involving the time constant tend to involve
  • Calculations
  • Determining the time constant from a graph
• To find the time constant from a voltage-time graph, calculate 0.37V₀ and determine the corresponding time for that value

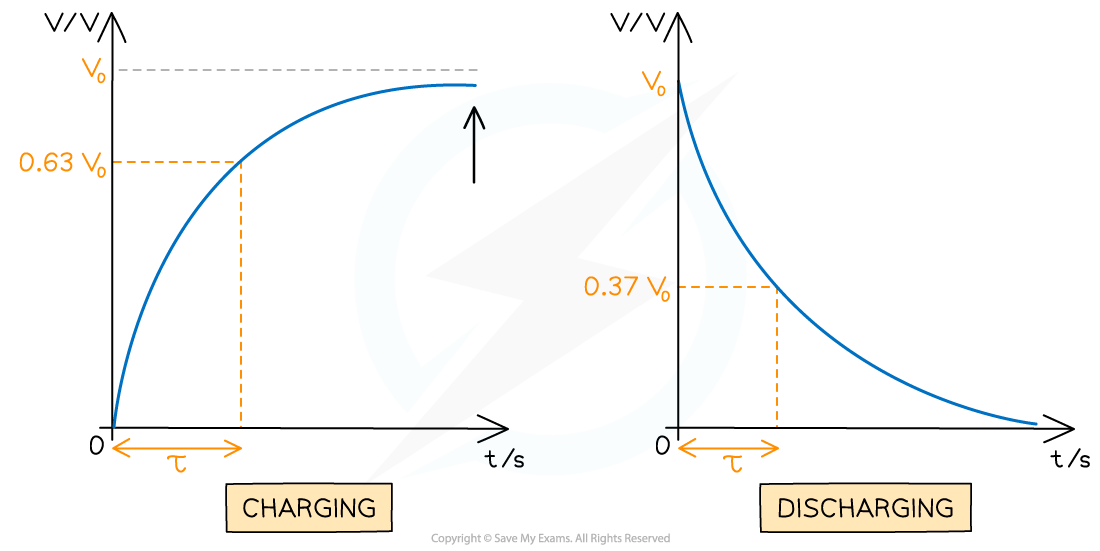
The time constant shown on a charging and discharging capacitor

Worked Example