12.2.1 Rutherford Scattering & Nuclear Radius

• In the Rutherford scattering experiment, alpha particles are fired at a thin gold foil
• Initially, before interacting with the foil, the particles have kinetic energy, 

• Some of the alpha particles are found to come straight back from the gold foil
• This indicates that there is electrostatic repulsion between the alpha particles and the gold nucleus

Experimental set up of the Rutherford alpha scattering experiment

• At the point of closest approach, d, the repulsive force reduces the speed of the alpha particles to zero momentarily, before any change in direction
  • At this point, the initial kinetic energy of an alpha particle, E_k, is equal to electric potential energy, E_p
• The radius of the closest approach can be found be equating the initial kinetic energy to the electric potential energy

• Where:
  • Charge of an alpha particle, Q = 2e
  • Charge of a target nucleus, q = Ze
  • Z = proton number
  • e = charge on an electron (or proton)
• Substituting into the equation:

• This gives an expression for the potential energy at the point of repulsion:

• Due to conservation of energy:
  • This expression also gives the initial kinetic energy possessed by the alpha particle

• Rearranging and calculating for the distance, d, gives a value for the radius of the nucleus when the alpha particle is fired with high energy

The closest approach method of determining the size of a gold nucleus

Nuclear Radius

• The radius of nuclei depends on the nucleon number, A of the atom
• This makes sense because as more nucleons are added to a nucleus, more space is occupied by the nucleus, hence giving it a larger radius
• The exact relationship between the radius and nucleon number can be determined from experimental data
• By doing this, physicists were able to deduce the following relationship:

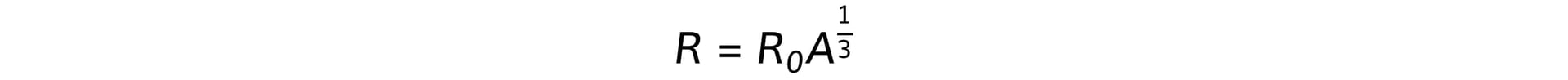
• Where:
  • R = nuclear radius (m)
  • A = nucleon / mass number
  • R₀ = constant of proportionality = 1.20 fm

Nuclear Density

• Assuming that the nucleus is spherical, its volume is equal to:

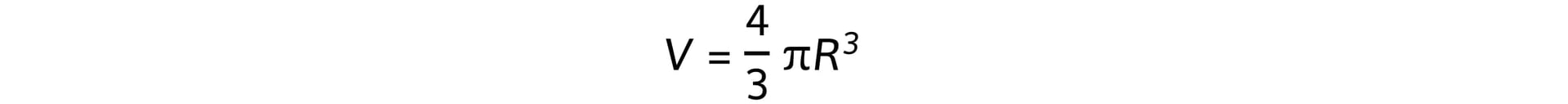
• Where R is the nuclear radius, which is related to mass number, A, by the equation:

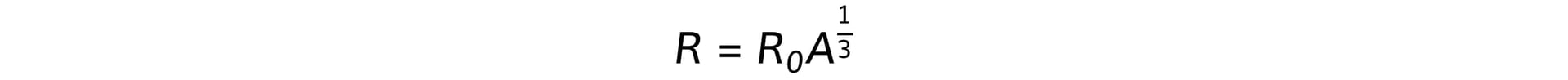
• Where R₀ is a constant of proportionality

• Combining these equations gives:

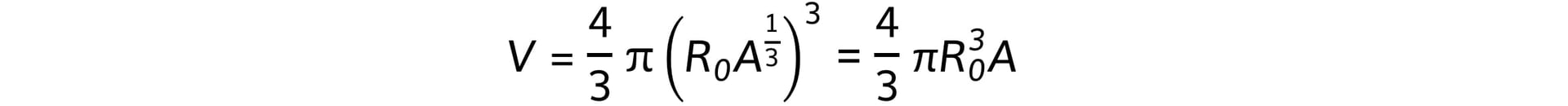
• Therefore, the nuclear volume, V, is proportional to the mass of the nucleus, A

• Mass (m), volume (V), and density (ρ) are related by the equation:

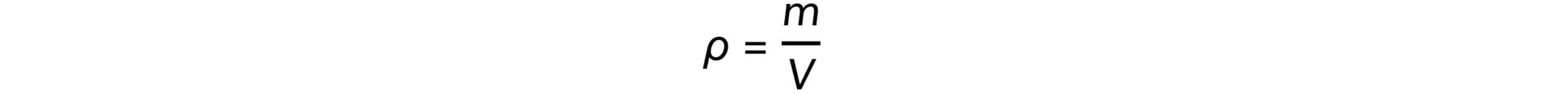
• The mass, m, of a nucleus is equal to:

m = Au

• Where:
  • A = the mass number
  • u = atomic mass unit

• Using the equations for mass and volume, nuclear density is equal to:

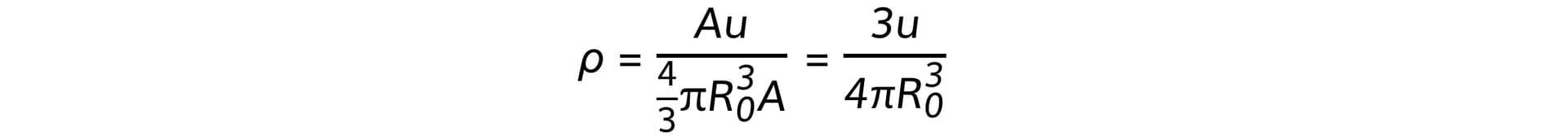
• Since the mass number A cancels out, the remaining quantities in the equation are all constant

• Therefore, this shows the density of the nucleus is:
  • Constant
  • Independent of the radius

• The fact that nuclear density is constant shows that nucleons are evenly separated throughout the nucleus regardless of their size

• The accuracy of nuclear density depends on the accuracy of the constant R₀, as a guide nuclear density should always be of the order 10¹⁷ kg m^–3
• Nuclear density is significantly larger than atomic density, this suggests:
  • The majority of the atom’s mass is contained in the nucleus
  • The nucleus is very small compared to the atom
  • Atoms must be predominantly empty space

Worked Example

• • Using the equation derived above, the density of the nucleus is:

Exam Tip