9.3.2 Two-Slit Interference Patterns

• For two-source interference fringes to be observed, the sources of the wave must be:
  • Coherent (constant phase difference)
  • Monochromatic (single wavelength)

• When two waves interfere, the resultant wave depends on the phase difference between the two waves
  • This is proportional to the phase difference between the waves which can be written in terms of the wavelength λ of the wave

• As seen from the diagram, the wave from slit S₂ has to travel slightly further than that from S₁ to reach the same point on the screen
  • The difference in this distance is the path difference

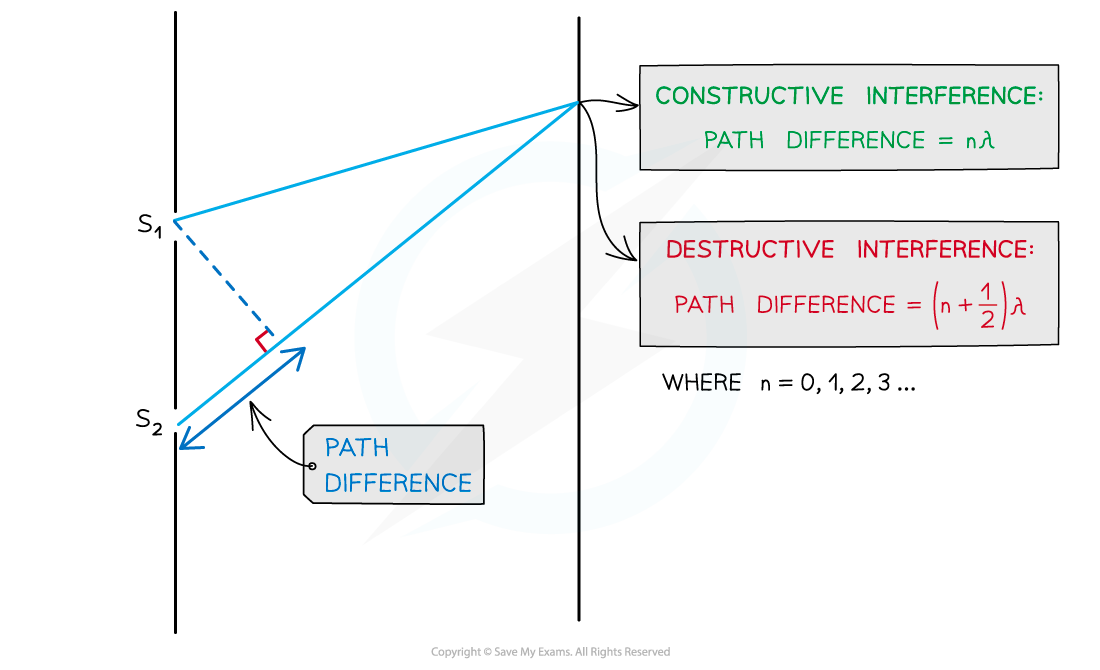
Interference is caused by the variation in path length between the two slits

 

• For constructive interference (or maxima), the difference in wavelengths will be an integer number of whole wavelengths
• The condition for constructive interference can be written as:

path difference =  (where n = 0, 1, 2, 3 ...)

• When waves undergo constructive interference their amplitudes add to form a resultant combined wave at the point where they meet

---

• For destructive interference (or minima) it will be an integer number of whole wavelengths plus a half wavelength
• The condition for destructive interference can be written as:

path difference =  (where n = 0, 1, 2, 3 ...)

• n is the order of the maxima (bright fringes) / minima (dark fringes)
  • n = 0 is taken from the middle, n = 1 is the next peak and so on
• When waves undergo destructive interference their amplitudes subtract to form a resultant combined wave at the point where they meet

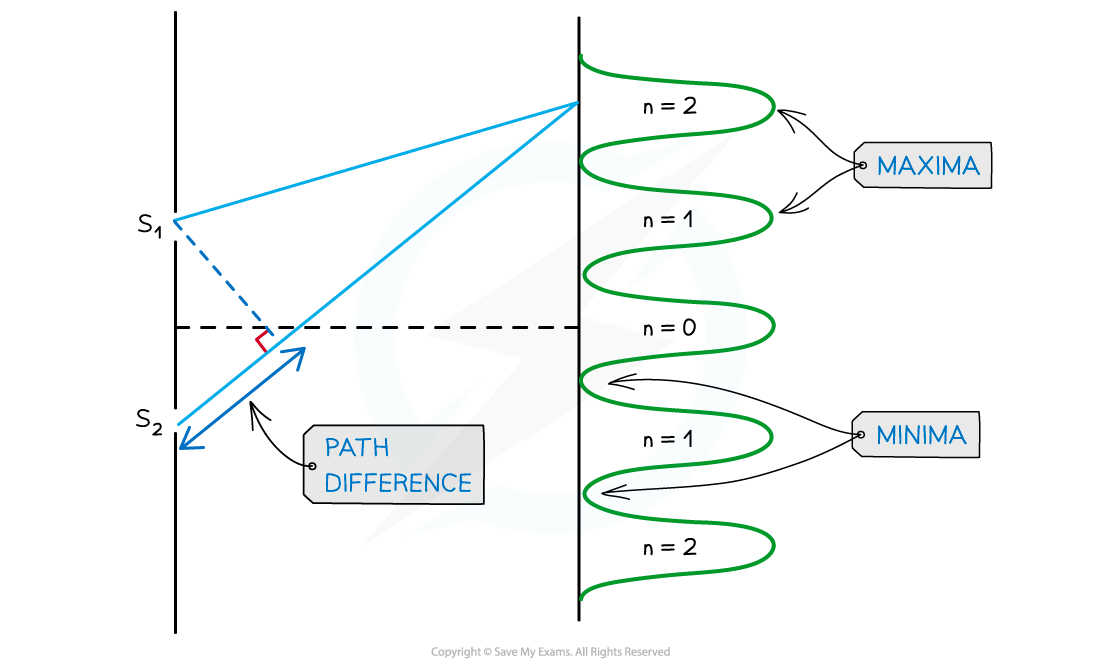
Interference pattern of light waves shown with orders of maxima and minima

• An interference pattern shows the intensity of light at different distances away from the central maxima
  • For a double-slit interference pattern the intensity of the light is the same for all maxima
• This is different to the double-slit diffraction pattern that is observed on a screen (These are explained in 9.3.3 Diffraction Grating Patterns)

Double-Slit Diffraction Geometry

• The diffraction pattern made by waves passing through two slits of separation d can be observed on a screen placed a large distance, D, away

• If the distance, D, between the slits and the screen is considerably larger than the slit separation, :
  • The light rays can be considered as a set of plane wavefronts that are parallel to each other

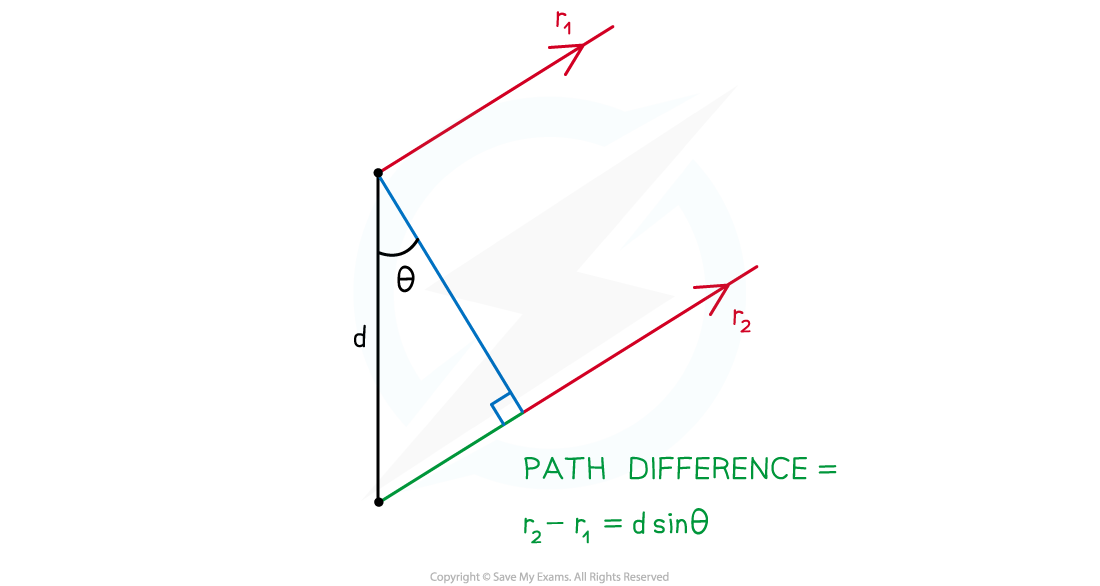
• For two paths, r₁ and r₂, travelling parallel to each other at an angle, θ, between the normal and the slit, the path difference will be:

path difference = r₂ − r₁ = 

• For constructive interference:

path difference =

• Therefore, bright fringes will occur when:

• For destructive interference:

path difference =

• Therefore, dark fringes will occur when:

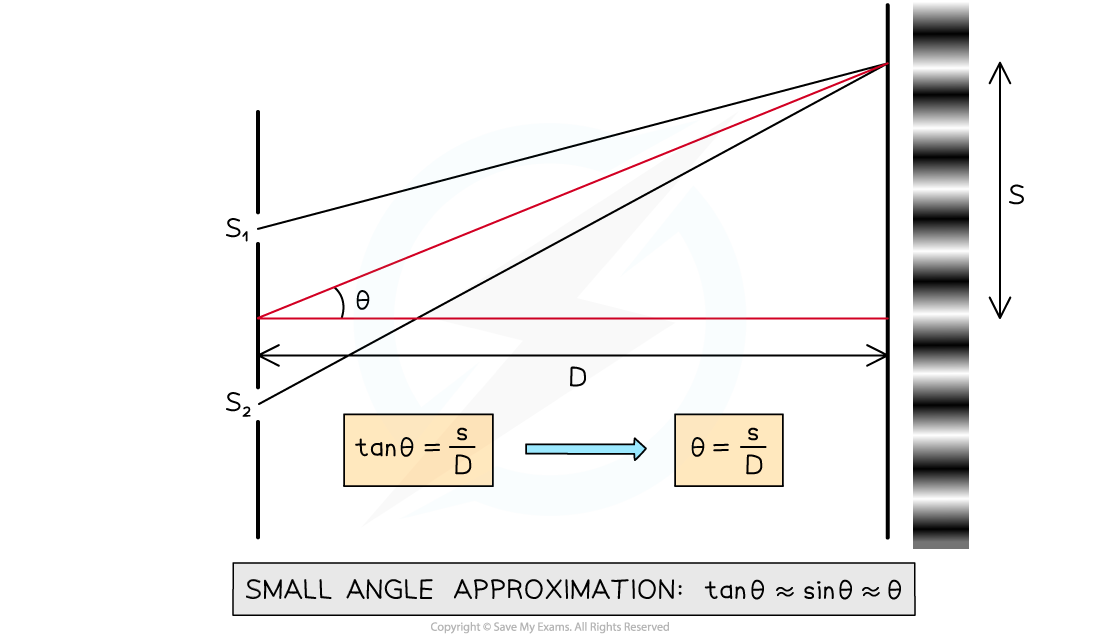
• The distance between fringes, s, can be related to the distance to the screen, D, using trigonometry:

• Since the angle θ is small, the small-angle approximation may be used:

• Using the condition for constructive interference and the small-angle approximation:

• Rearrange the equation for θ:

• Combining the two equations gives:

• Rearranging for s gives an equation for the distance between two maxima:

Exam Tip

• In single slit diffraction, the observed interference pattern shows:
  • A central maximum with the highest intensity
  • Subsequent maxima with half the width of the central maximum
  • The intensity of each subsequent maxima decreases

• In double slit diffraction, the observed interference pattern shows: 
  • The fringes are equally bright, meaning they have equal intensity
  • The angle increases by a constant amount, as the fringes are equally separated
• Note: this is only the case for double slit diffraction for slit widths of negligible size

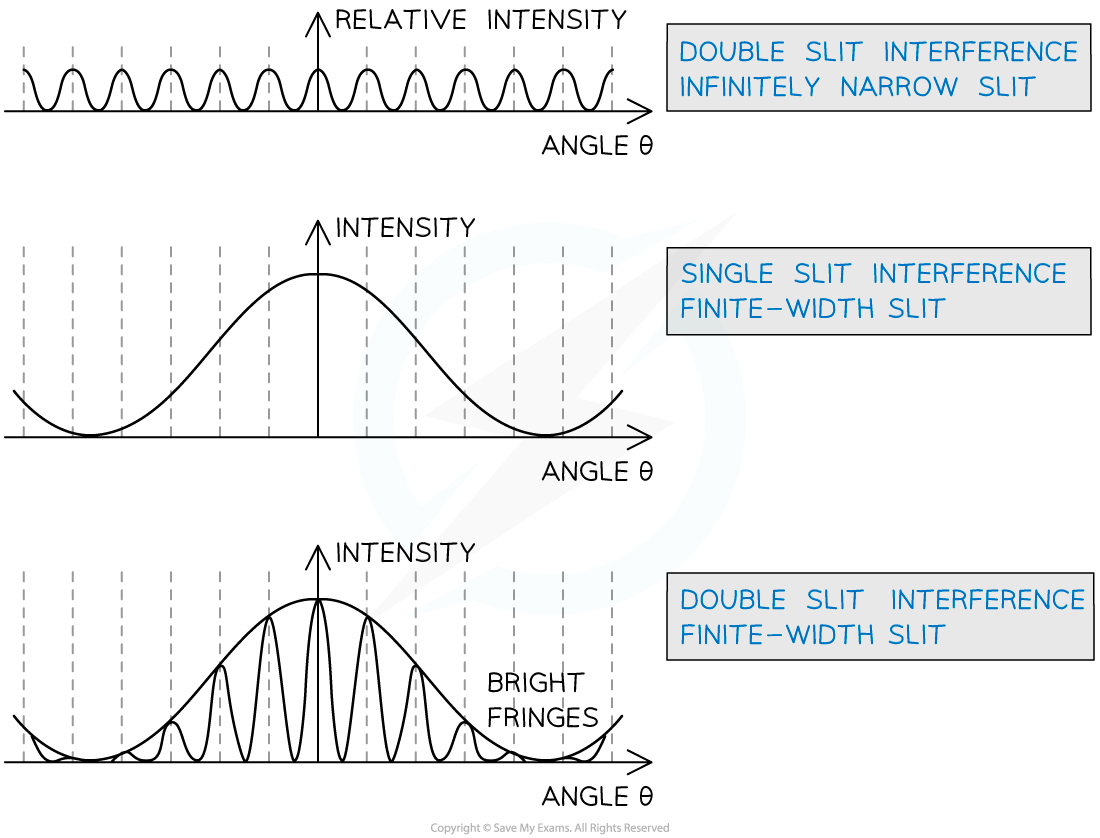
Intensity graphs for single and double slit interference when the slit is infinitely narrow compared to a slit of finite width

• The fringes due to the double slits are much closer together than in the single slit case
  • This is because the distance between the slits is greater than their widths

• The resulting interference pattern is a combination of the double-slit and single slit interference patterns 
  • This is known as modulation

 

A modulated double-slit interference pattern with the single slit diffraction pattern is still visible in the "envelope" (shown by the dotted line). This occurs when the slit width is significant. 

• The intensity of the resulting fringe pattern has been modulated by the interference of the two diffracted beams, as the effect of the single slits is significant
• This is assuming that:
  • The slit width is not negligible
  • The distance between the slits is much greater than their width