Solving Vector Problems
- In physics, vectors appear in many different topic areas
- Specifically, vectors are often combined and resolved to solve problems when considering motion, forces, and momentum
Forces on an Inclined Plane
- Objects on an inclined plane is a common scenario in which vectors need to be resolved
- An inclined plane, or a slope, is a flat surface tilted at an angle, θ
- Instead of thinking of the component of the forces as horizontal and vertical, it is easier to think of them as parallel or perpendicular to the slope
- The weight of the object is vertically downwards and the normal (or reaction) force, R is always vertically up from the object
- The weight W is a vector and can be split into the following components:
- W cos (θ) perpendicular to the slope
- W sin (θ) parallel to the slope
- If there is no friction, the force W sin (θ) causes the object to move down the slope
- If the object is not moving perpendicular to the slope, the normal force will be R = W cos (θ)
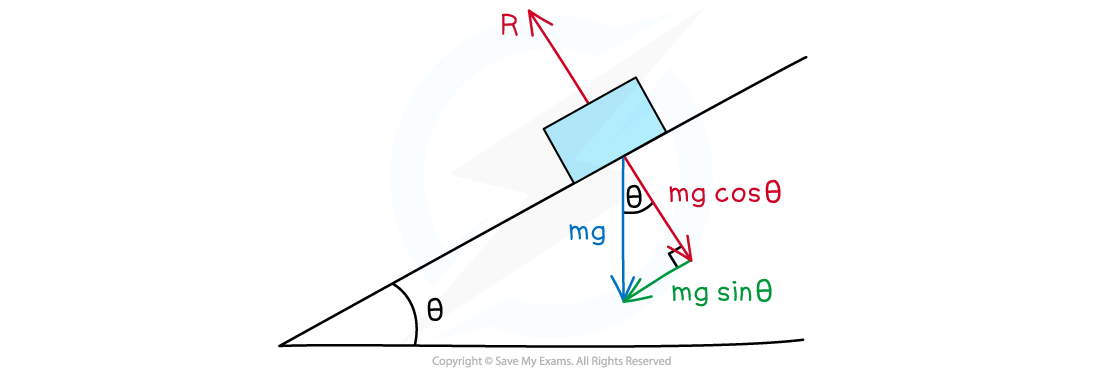
The weight vector of an object on an inclined plane can be split into its components parallel and perpendicular to the slope
Worked Example
A helicopter provides a lift of 250 kN when the blades are tilted at 15º from the vertical. Calculate the horizontal and vertical components of the lift force.
Calculate the horizontal and vertical components of the lift force.
Step 1: Draw a vector triangle of the resolved forces
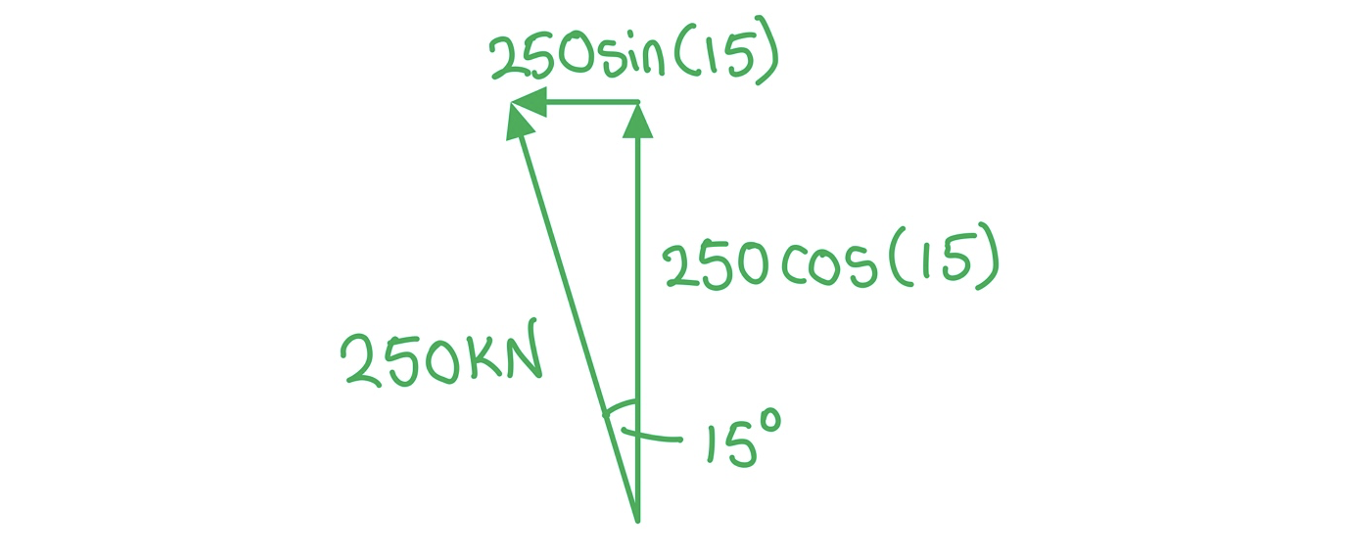
Step 2: Calculate the vertical component of the lift force
Vertical = 250 × cos(15) = 242 kN
Step 3: Calculate the horizontal component of the lift force
Horizontal = 250 × sin(15) = 64.7 kN
Worked Example
A person is exploring a new part of town, from their starting point they walk 100 m in the direction 30.0º South of West. They then walk 200 m in the direction 40.0º degrees South of East and finally they walk 150 m directly East. Calculate the magnitude of their displacement from their original position.
Calculate the magnitude of their displacement from their original position.
In order to calculate the answer, the vectors of displacement must be resolved into their x-components and y-components and then combined. In this case, this effectively means the x-direction is East-West and the y-direction is North-South
Step 1: Consider positive and negative directions for reference
- Since East is likely to be larger consider it the positive displacement and West as negative
- Similarly, consider South as positive and North as negative
Step 2: Resolve the first displacement (100 m magnitude) into its components
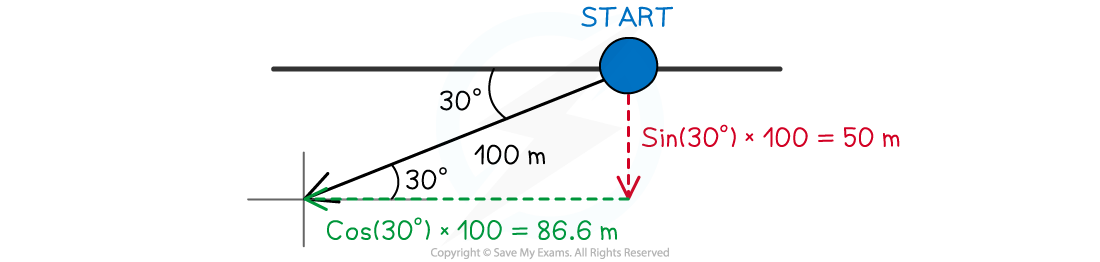
- The horizontal component can be resolved from:
cos(30°) × 100 = 86.6 m
- This is in a Western (negative horizontal) direction
- The vertical component can be resolved from:
sin(30°) × 100 = 50.0 m
- This is in a Southern (positive vertical) direction
Step 3: Resolve the second displacement (200 m magnitude) into its components

- The horizontal component can be resolved from:
cos(40°) × 200 = 153 m
- This is in an Eastern (positive horizontal) direction
- The vertical component can be resolved from:
sin(40°) × 200 = 129 m
- This is in a Southern (positive vertical) direction
Step 4: Resolve the third displacement (150 m magnitude) into its components
- The horizontal component is already resolved into
150 m
- This is in an Eastern (positive horizontal) direction
- There is no vertical component for this vector
Step 5: Combine the horizontal (East-West) components
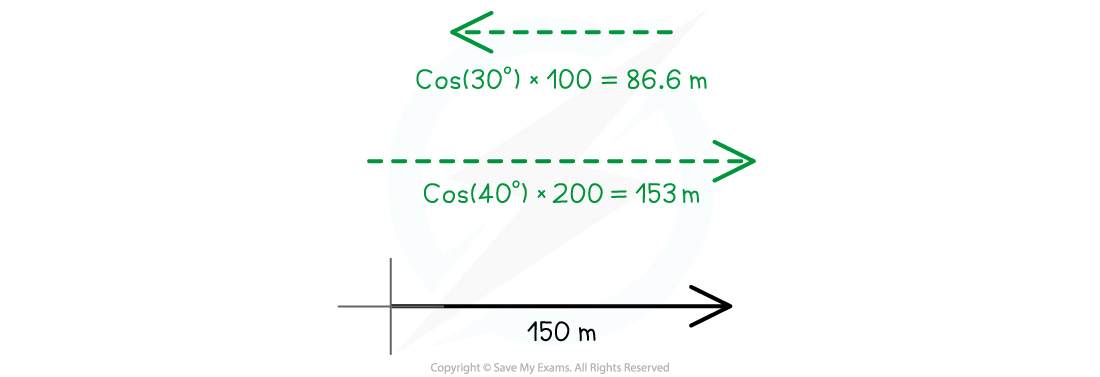
153 + 150 - 86.6 = 166 m
- This is in an Eastern (positive horizontal) direction
Step 6: Combine the vertical (North-South) components
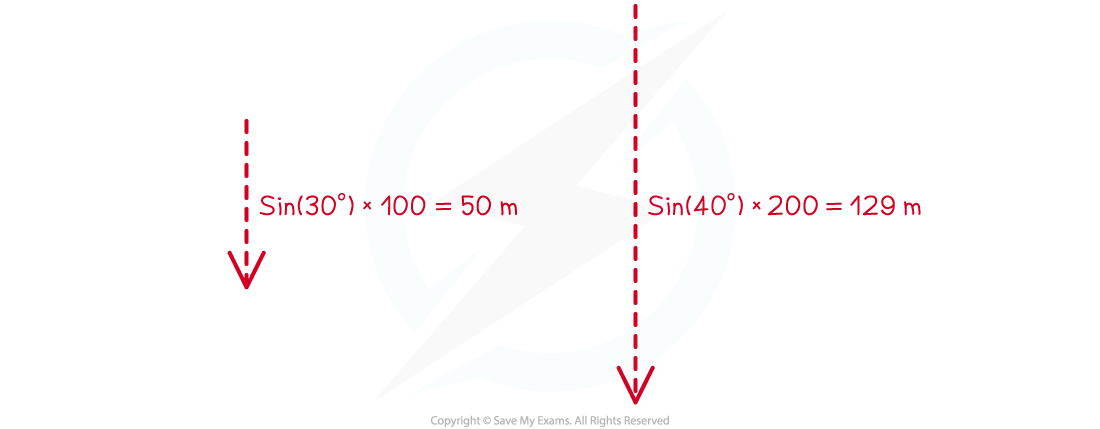
50.0 + 129 = 170 m
- This is in a Southern (positive vertical) direction
Step 7: Using Pythagoras theorem to find the resultant hypotenuse vector
√(1662 + 1792) = 244 m
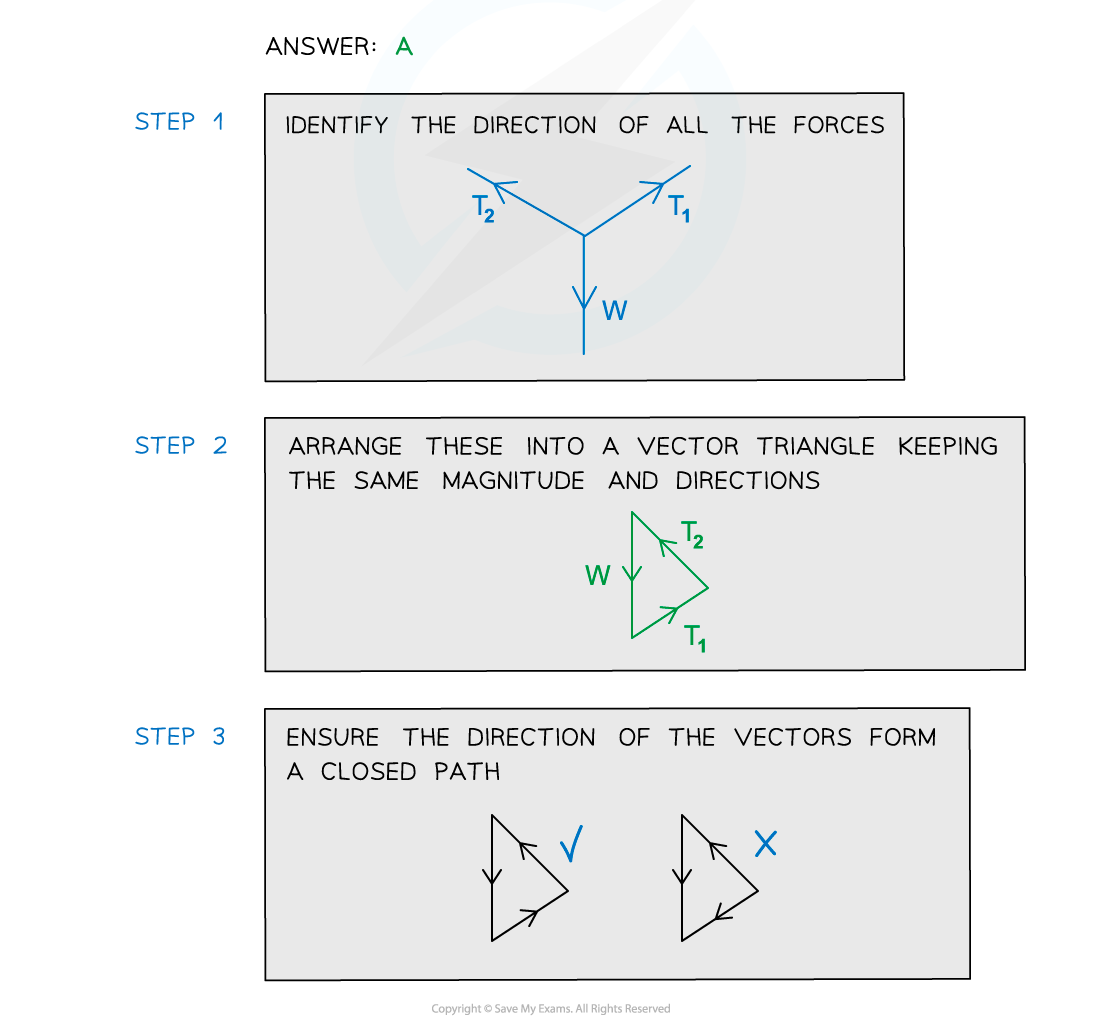
Equilibrium
- Coplanar forces can be represented by vector triangles
- Forces are in equilibrium if an object is either
- At rest
- Moving at constant velocity
- In equilibrium, coplanar forces are represented by closed vector triangles
- The vectors, when joined together, form a closed path
- The most common forces on objects are
- Weight
- Normal reaction force
- Tension (from cords and strings)
- Friction
- The forces on a body in equilibrium are demonstrated below:
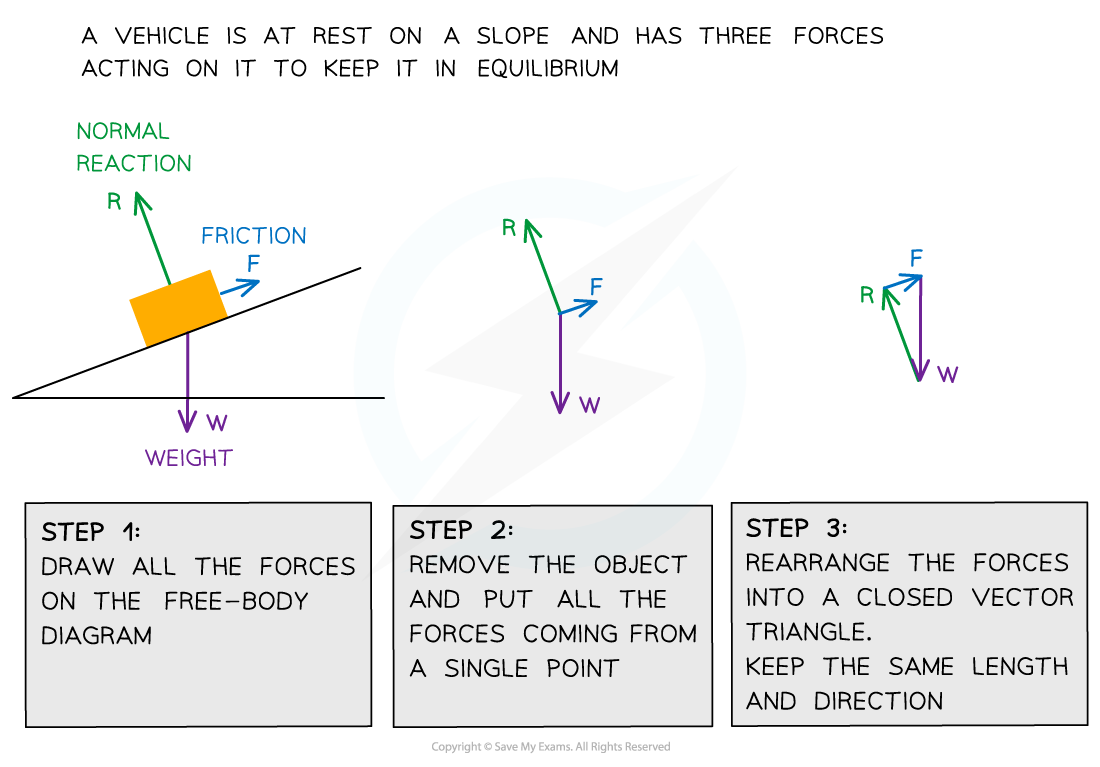
Three forces on an object in equilibrium form a closed vector triangle
Worked Example
A weight hangs in equilibrium from a cable at point X. The tensions in the cables are T1 and T2 as shown. Which diagram correctly represents the forces acting at point X?
Which diagram correctly represents the forces acting at point X?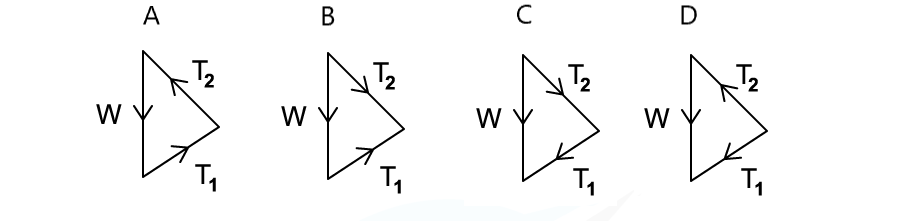
Exam Tip
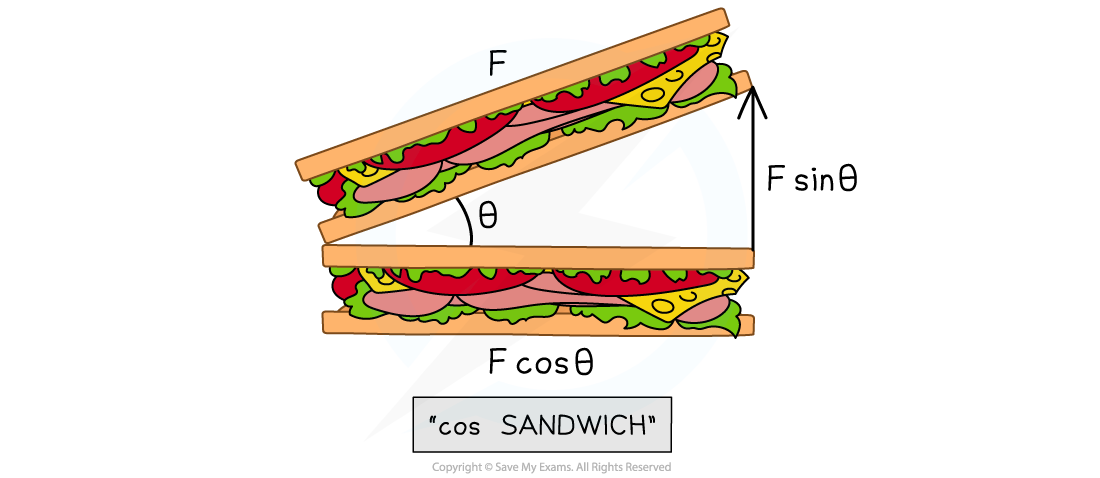
If you're unsure as to which component of the force is cos θ or sin θ, just remember that the cos θ is always the adjacent side of the right-angled triangle AKA, making a 'cos sandwich'