Orbital Motion, Speed & Energy
- Since most planets and satellites have a near circular orbit, the gravitational force FG between the sun or another planet provides the centripetal force needed to stay in an orbit
- Both the gravitational force and centripetal force are perpendicular to the direction of travel of the planet
- Consider a satellite with mass m orbiting Earth with mass M at a distance r from the centre travelling with linear speed v
FG = Fcirc
- Equating the gravitational force to the centripetal force for a planet or satellite in orbit gives:
- The mass of the satellite m will cancel out on both sides to give:
- Where:
- v = linear speed of the mass in orbit (m s-1)
- G = Newton's Gravitational Constant
- M = mass of the object being orbited (kg)
- r = orbital radius (m)
- This means that all satellites, whatever their mass, will travel at the same speed v in a particular orbit radius r
- Since the direction of a planet orbiting in circular motion is constantly changing, the centripetal acceleration acts towards the planet
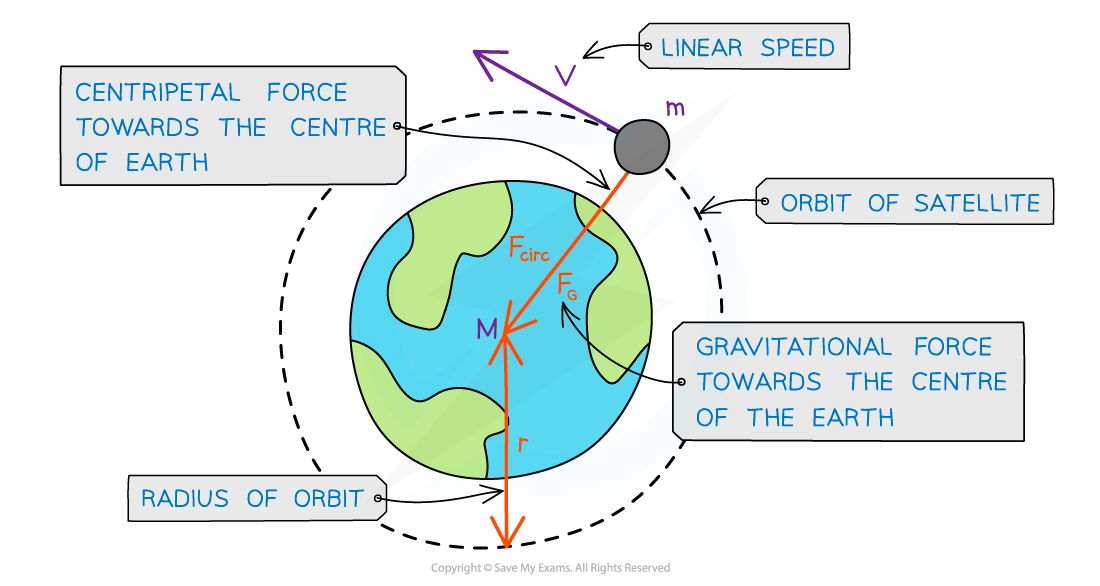
A satellite in orbit around the Earth travels in circular motion
Time Period & Orbital Radius Relation
- Since a planet or a satellite is travelling in circular motion when in order, its orbital time period T to travel the circumference of the orbit 2πr, the linear speed v is:
- This is a result of the well-known equation, speed = distance / time and first introduced in the circular motion topic
- Substituting the value of the linear speed v from equating the gravitational and centripetal force into the above equation gives:
- Squaring out the brackets and rearranging for T2 gives the equation relating the time period T and orbital radius r:
- Where:
- T = time period of the orbit (s)
- r = orbital radius (m)
- G = Newton's Gravitational Constant
- M = mass of the object being orbited (kg)
- The equation shows that the orbital period T is related to the radius r of the orbit. This is also known as Kepler’s third law:
For planets or satellites in a circular orbit about the same central body, the square of the time period is proportional to the cube of the radius of the orbit
- Kepler’s third law can be summarised as:
Graphical Representation of T2 ∝ r3
- The relationship between T and r can be shown using a logarithmic plot
- T2 ∝ r3
- 2 × log(T) ∝ 3 × log(r)
- The graph of log(T) in years against log(r) in AU (astronomical units) for the planets in our solar system is a straight line graph:
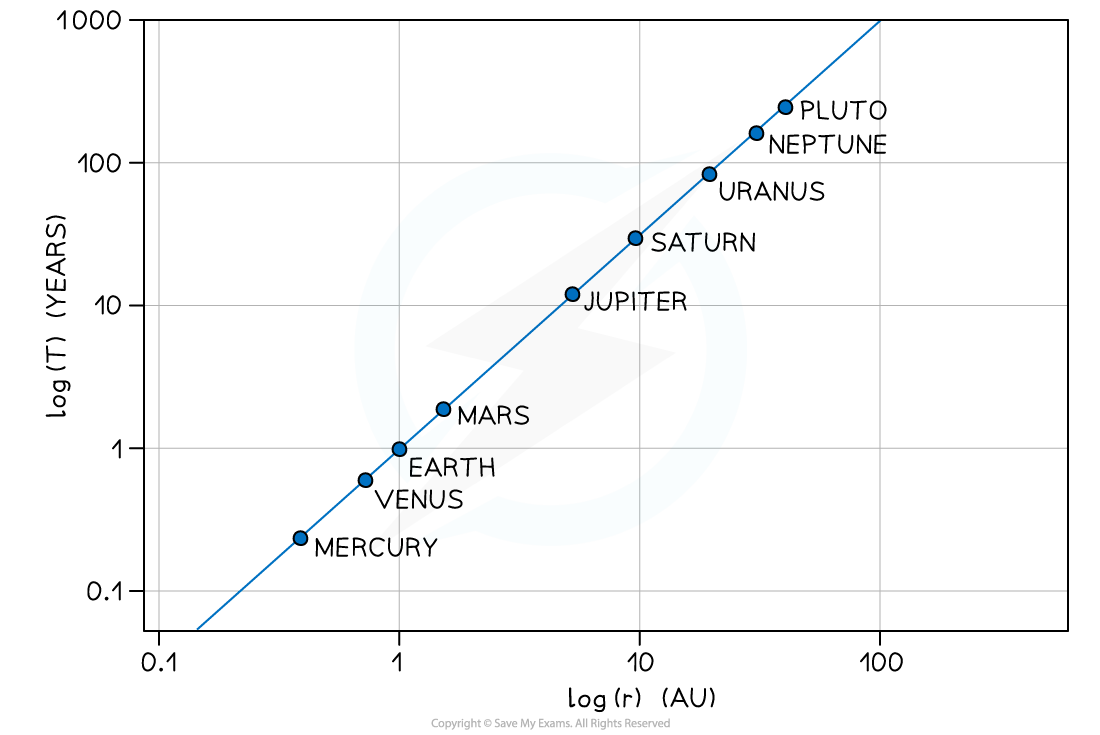
- The graph does not go through the origin since it has a negative y-intercept
- Only the log of both T and r will produce a straight line graph
Worked Example
A binary star system constant of two stars orbiting about a fixed point B. The star of mass M1 has a circular orbit of radius R1 and mass M2 has a radius of R2. Both have linear speed v and an angular speed ⍵ about B.
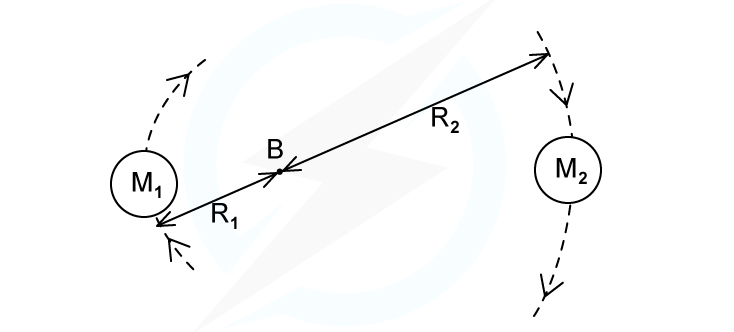
State the following formula, in terms of G, M2, R1 and R2
(i) The angular speed ⍵ of M1
(ii) The time period T for each star in terms of angular speed ⍵


Energy of an Orbiting Satellite
- An orbiting satellite follows a circular path around a planet
- Just like an object moving in circular motion, it has both kinetic energy (KE) and gravitational potential energy (GPE) and its total energy is always constant
- An orbiting satellite's total energy is calculated by:

A graph showing the kinetic, potential and total energy for a mass at varying orbital distances from a massive body
Total energy = Kinetic energy + Gravitational potential energy
- This means that the satellite's KE and GPE are also both constant in a particular orbit
- If the orbital radius of a satellite decreases its KE increases and its GPE decreases
- If the orbital radius of a satellite increases its KE decreases and its GPE increases
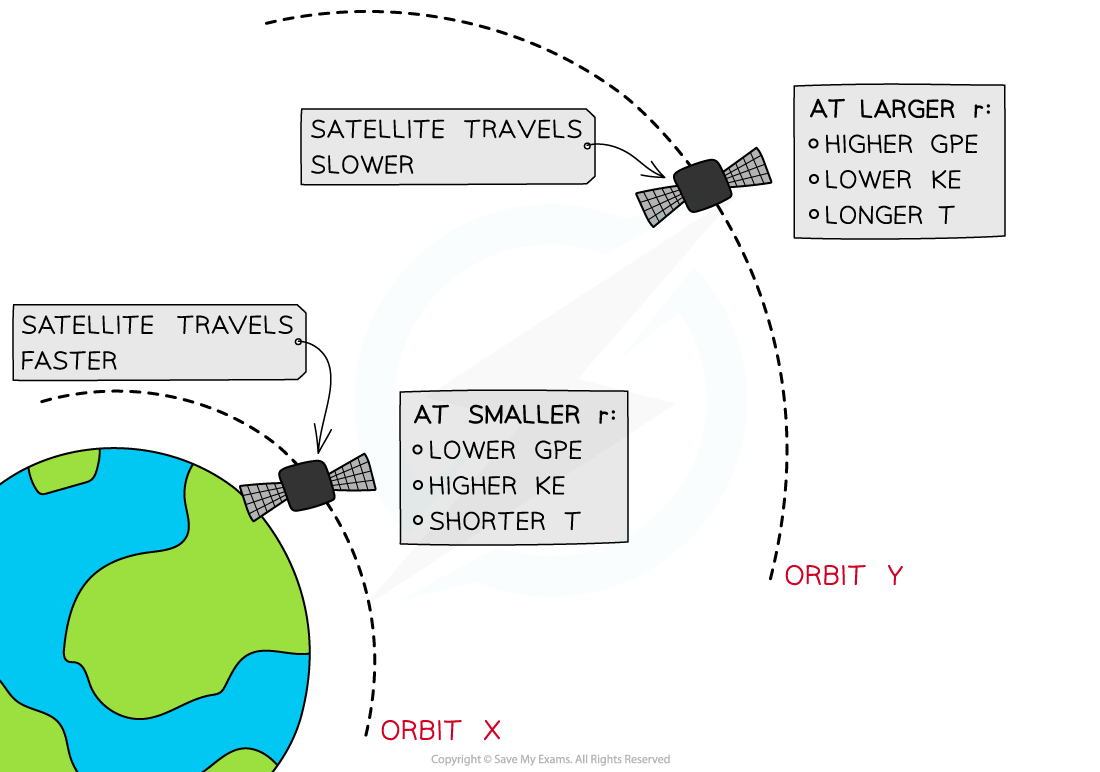
At orbit Y, the satellite has greater GPE and less KE than at at orbit X
- A satellite is placed in two orbits, X and Y, around Earth
- At orbit X, where the radius of orbit r is smaller, the satellite has a:
- Larger gravitational force on it
- Higher speed
- Higher KE
- Lower GPE
- Shorter orbital time period, T
- At orbit Y, where the radius of orbit r is larger, the satellite has a:
- Smaller gravitational force on it
- Smaller speed
- Lower KE
- Higher GPE
- Longer orbital time period, T
Worked Example
Two satellites A and B, of equal mass, orbit a planet at radii R and 3R respectively. Which one of the following statements is incorrect?
A A has more kinetic energy and less potential energy than B
B A has a shorter time period and travels faster than B
C B has less kinetic energy and more potential energy than A
D B has a longer time period and travels faster than A
ANSWER: D
-
- Since B is at a larger orbital radius (3R instead of R) it has a longer time period since T2 ∝ R3 for an orbiting satellite
- However, satellite B will travel much slower than A
- Its larger orbital radius means the force of gravity will be much lower for B than for A
Exam Tip
Orbital Energy Calculations
- A synchronous orbit is:
When an orbiting body has a time period equal to that of the body being orbited and in the same direction of rotation as that body
- These usually refer to satellites (the orbiting body) around planets (the body being orbited)
- The orbit of a synchronous satellite can be above any point on the planet's surface and in any plane
- When the plane of the orbit is directly above the equator, it is known as a geosynchronous orbit
Geostationary Orbit
- Many communication satellites around Earth follow a geostationary orbit
- This is sometimes referred to as a geosynchronous orbit
- This is a specific type of orbit in which the satellite:
- Remains directly above the equator
- Is in the plane of the equator
- Always orbits at the same point above the Earth’s surface
- Moves from west to east (same direction as the Earth spins)
- Has an orbital time period equal to Earth’s rotational period of 24 hours
- Geostationary satellites are used for telecommunication transmissions (e.g. radio) and television broadcast
- A base station on Earth sends the TV signal up to the satellite where it is amplified and broadcast back to the ground to the desired locations
- The satellite receiver dishes on the surface must point towards the same point in the sky
- Since the geostationary orbits of the satellites are fixed, the receiver dishes can be fixed too
Low Orbits
- Some satellites are in low orbits, which means their altitude is closer to the Earth's surface
- One example of this is a polar orbit, where the satellite orbits around the north and south pole of the Earth
- Low orbits are useful for taking high-quality photographs of the Earth's surface. This could be used for:
- Weather
- Military applications
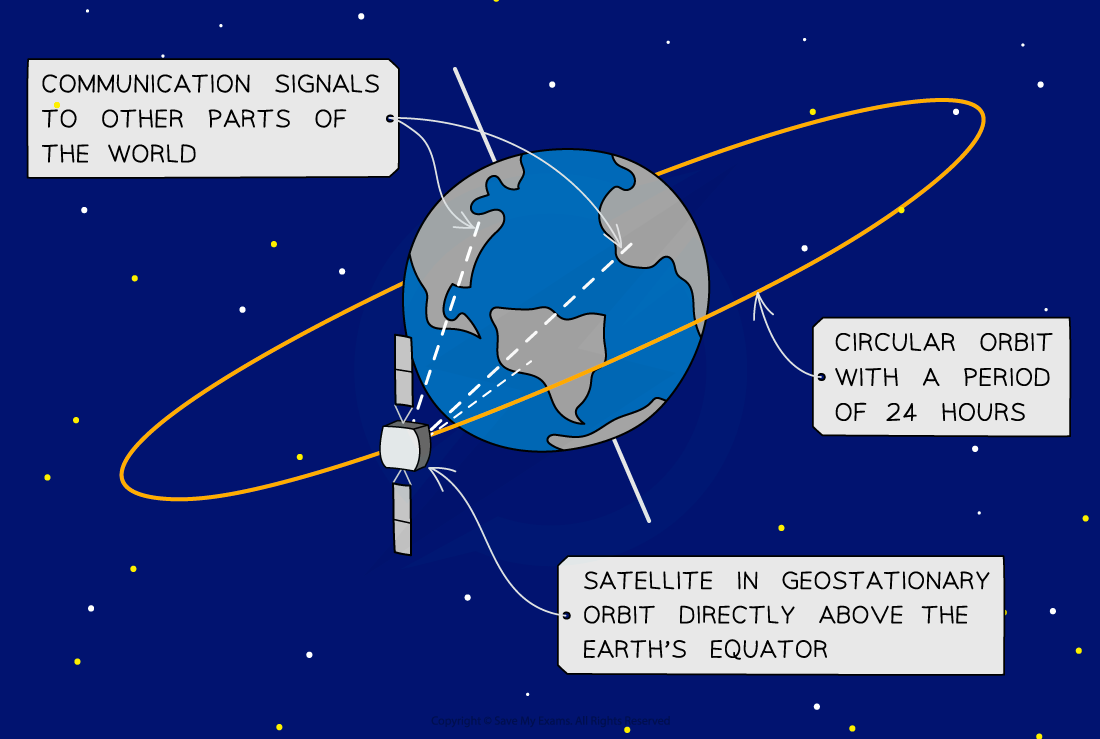
Geostationary satellite in orbit
Worked Example
Orbital Motion
- When a satellite is moving in orbital motion, the velocity of the satellite will be given by:
- Where
- vsatellite = velocity of the satellite (m s-1)
- M = mass of the Earth (or large body being orbited) (kg)
- G = The gravitational constant = 6.67 x 10-11 Nm2kg-2
- r = the orbital radius of the satellite (m)
- Therefore the kinetic energy of the satellite will be:
- Where
- EK = kinetic energy (J)
- v = velocity (m s-1)
- M = mass of the Earth (or large body being orbited) (kg)
- m = mass of satellite or orbiting object (kg)
- G = The gravitational constant = 6.67 x 10-11 Nm2kg-2
- r = the orbital radius of the satellite (m)
- The gravitational potential energy of an orbiting object is:
- Where
- EP = potential energy (J)
- M = mass of the Earth (or large body being orbited) (kg)
- m = mass of satellite or orbiting object (kg)
- G = The gravitational constant = 6.67 x 10-11 Nm2kg-2
- r = the orbital radius of the satellite (m)
- The total energy for any satelite orbiting a massive body is found from the combination of potential energy and kinetic energy
- The result is show in the equation below:
- Where
- ET = The total energy of the satellite (J)
- EP = The potential energy of the satellite (J)
- EK = The kinetic energy of the satellite (J)
- v = the velocity of the satellite (m s-1)
- M = mass of the Earth (or large body being orbited) (kg)
- m = mass of satellite or orbiting object (kg)
- G = The gravitational constant = 6.67 x 10-11 Nm2kg-2
- r = the orbital radius of the satellite (m)

