Orders of Magnitude
- When a number is expressed in an order of 10, this is an order of magnitude.
- Example: If a number is described as 3 × 108 then that number is actually 3 × 100 000 000
- The order of magnitude of 3 × 108 is just 108
- Orders of magnitude follows rules for rounding
- The order of magnitude of 6 × 108 is 109 as the magnitude is rounded up
- A quantity is an order of magnitude larger than another quantity if it is about ten times larger
- Similarly, two orders of magnitude would be 100 times larger, or 102
- In physics, orders of magnitude can be very large or very small
- When estimating values, it’s best to give the estimate of an order of magnitude to the nearest power of 10
- For example, the diameter of the Milky Way is approximately 1 000 000 000 000 000 000 000 m
- It is inconvenient to write this many zeros, so it’s best to use scientific notation as follows:
1 000 000 000 000 000 000 000 = 1 × 1021 m
- The order of magnitude is 1021
- Orders of magnitude make it easier to compare the relative sizes of objects
- For example, a quantity with an order of magnitude of 106 is 10 000 times larger than a quantity with a magnitude of 102
Estimating Physical Quantities Table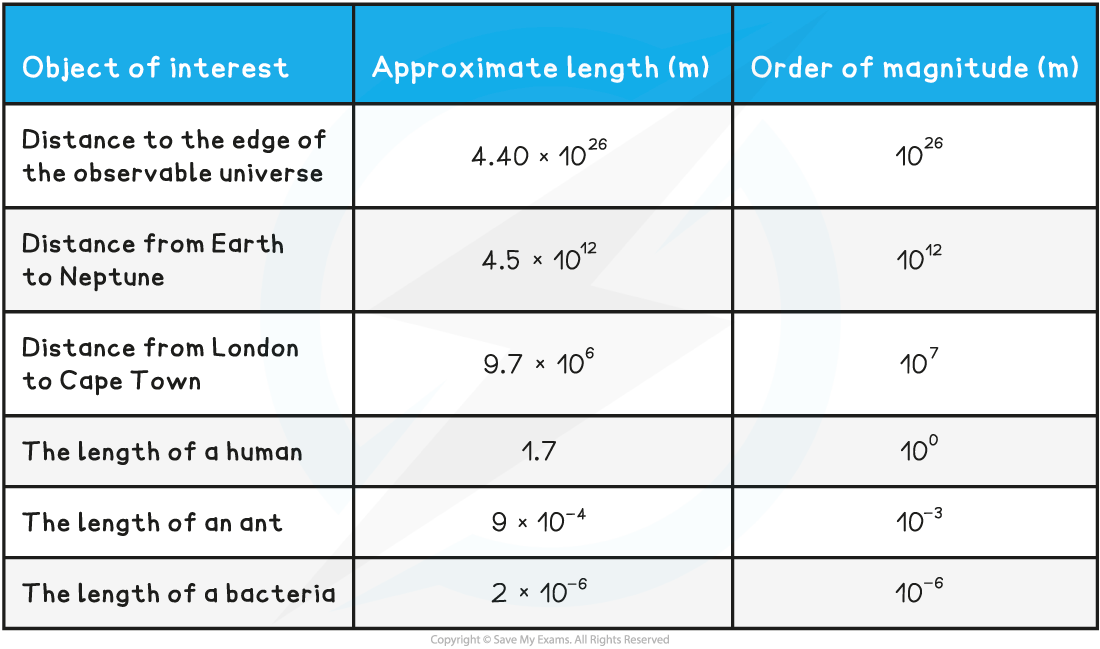
Estimating Physical Quantities
- To estimate is to obtain an approximate value
- For very large or small quantities, using orders of magnitudes to estimate calculations is a valid approach
- Estimation is typically done to the nearest order of magnitude
Worked Example
Estimate the order of magnitude of the following:
a) The temperature of an oven (in Kelvin)
b) The volume of the Earth (in m3)
c) The number of seconds in a person's life if they live to be 95 years old
Part (a)
The temperature of the oven:
Step 1: Identify the approximate temperature of an oven
- A conventional oven works at ∼200 °C which is 473 K
Step 2: Identify the order of magnitude
- Since this could be written as 4.73 × 102 K
- The order of magnitude is ∼102
Part (b)
The volume of the Earth (in m3):
Step 1: Identify the approximate radius of the Earth
- The radius of the Earth is ∼6.4 × 106 m
Step 2: Use the radius to calculate the volume
- The volume of a sphere is equal to:
V = 4/3 π r3
V = 4/3 × π × (6.4 × 106)3
V = 1.1 × 1021 m3
Step 3: Identify the order of magnitude
- The order of magnitude is ∼1021
Part (c)
The number of seconds in 95 years:
Step 1: Find the number of seconds in a single year
1 year = 365 days with 24 hours each with 60 minutes with 60 seconds
365 × 24 × 60 × 60 = 31 536 000 seconds in a year
Step 2: Find the number of seconds in 95 years
95 × 31 536 000 = 283 824 000 seconds
- This is approximately 2.84 × 108 seconds
- Therefore the order of magnitude is ∼108
Exam Tip
When studying IB DP Physics, it is recommended to state your answer on a single line explicitly (if possible) with all necessary details to ensure the examiners can mark correctly and for best practice.
