Potential Energy Calculations
Electric Potential Energy of Two Point Charges
- The electric potential energy Ep at point in an electric field is defined as:
The work done in bringing a charge from infinity to that point
- The electric potential energy of a pair of point charges Q1and Q2 is defined by:
- Where:
- Ep = electric potential energy (J)
- r = separation of the charges Q1 and Q2 (m)
- ε0 = permittivity of free space (F m-1)
- The potential energy equation is defined by the work done in moving point charge Q2 from infinity towards a point charge Q1.
- The work done is equal to:
-
- Where:
- W = work done (J)
- V = electric potential due to a point charge (V)
- Q = Charge producing the potential (C)
- Where:
- This equation is relevant to calculate the work done due on a charge in a uniform field
- Unlike the electric potential, the potential energy will always be positive
- Recall that at infinity, V = 0 therefore Ep = 0
- It is more useful to find the change in potential energy, for example, as one charge moves away from another
-
- The change in potential energy from a charge Q1 at a distance r1 from the centre of charge Q2 to a distance r2 is equal to:
-
- The change in electric potential ΔV is the same, without the charge Q2
- There is another similarity with gravitational potential, as both equations are very similar to the change in gravitational potential between two points near a point mass
Worked Example
An -particle
is moving directly towards a stationary gold nucleus
.
At a distance of 4.7 × 10-15 m, the -particle momentarily comes to rest.
Calculate the electric potential energy of the particles at this instant.
Step 1: Write down the known quantities
-
- Distance, r = 4.7 × 10-15 m
- The charge of one proton, q = +1.60 × 10-19 C
An alpha particle (Helium nucleus) has 2 protons
-
- Charge of alpha particle, Q1 = 2 × 1.60 × 10-19 = +3.2 × 10-19 C
The gold nucleus has 79 protons
-
- Charge of gold nucleus, Q2 = 79 × 1.60 × 10-19 = +1.264 × 10-17 C
Step 2: Write down the equation for electric potential energy
Gravitational Potential Energy Between Two Point Masses
- The gravitational potential energy (G.P.E) at point in a gravitational field is defined as:
The work done in bringing a mass from infinity to that point
- The equation for G.P.E of two point masses m and M at a distance r is:
- G.P.E is calculated using mgh, but recall that at infinity, g = 0 and therefore G.P.E = 0
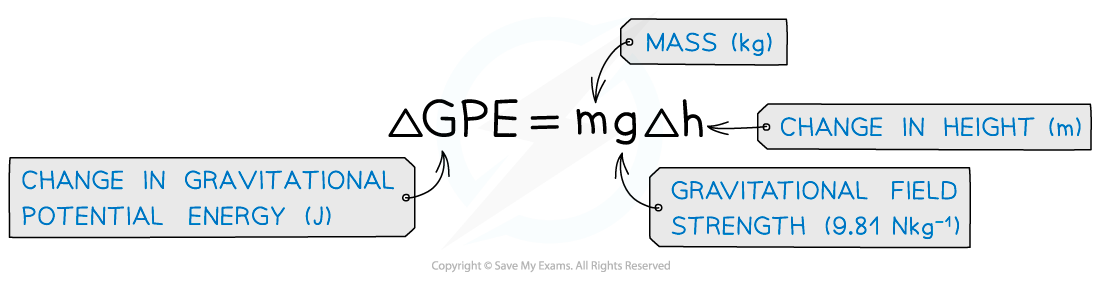
- It is more useful to find the change in G.P.E for example for a satellite which is lifted into space from the Earth’s surface
-
- The change in G.P.E from for an object of mass m at a distance r1 from the centre of mass M, to a distance of r2 further away is:
Change in gravitational potential energy between two points
-
- The change in potential Δg is the same, without the mass of the object m:
Change in gravitational potential between two points
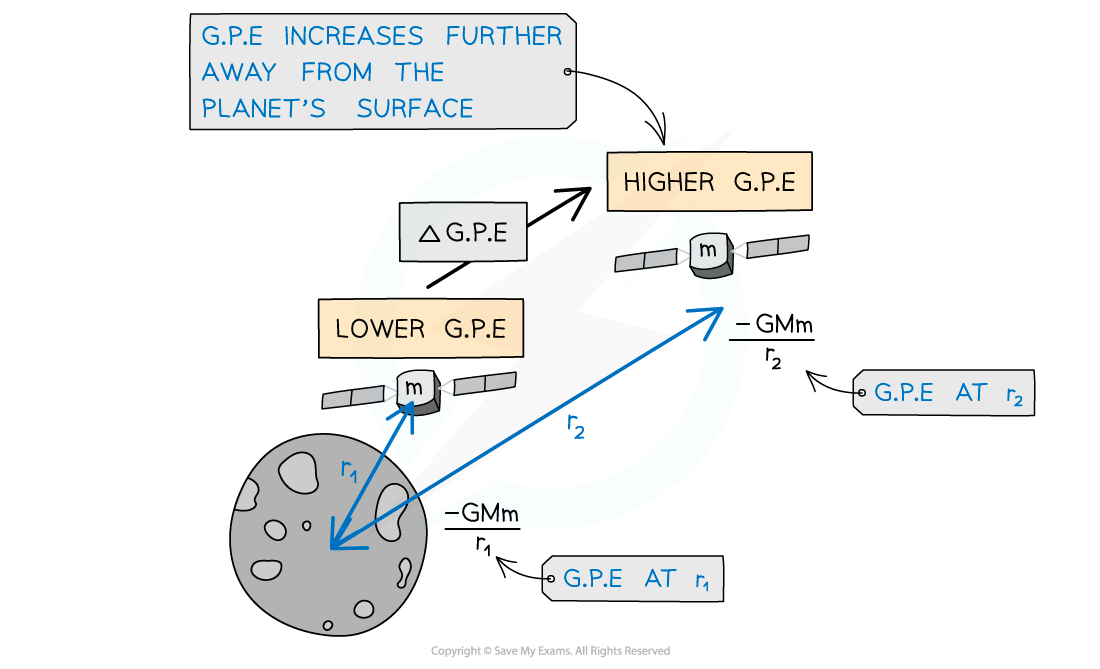
Gravitational potential energy increases as a satellite leaves the surface of the Moon
Worked Example
Calculate the difference in potential energy when a satellite of mass 1450 kg when it is moved from a distant orbit of 980 km above Earth’s surface to a closer orbit of 480 km above the Earth’s surface. Assume the Earth’s mass to be 5.97 x 1024 kg and the radius of the Earth to be 6.38 x 106 m.
-
- Initial distance of orbit above Earth’s surface: 980 km
- Final distance of orbit above Earth’s surface: 480 km
- Mass of the satellite: m = 1450 kg
- Earth’s mass: M = 5.97 x 1024 kg
- Radius of the Earth: 6.38 x 106 m
Step 3: Convert distances into standard units and include Earth radius
-
- Distance from centre of Earth to orbit 1:
9.8 x 105 m + 6.38 x 106 m = 7.36 x 106 m
-
- Distance from centre of Earth to orbit 2:
4.8 x 105 m + 6.38 x 106 m = 6.86 x 106 m
Step 4: Substitute values into the equation
Step 5: State final answer
-
- The difference in gravitational potential energy between the two orbits is: 5.72 x 109 J
