Combining & Resolving Vectors
- Vectors are represented by an arrow
- The arrowhead indicates the direction of the vector
- The length of the arrow represents the magnitude
Combining Vectors
- Vectors can be combined by adding or subtracting them to produce the resultant vector
- The resultant vector is sometimes known as the ‘net’ vector (eg. the net force)
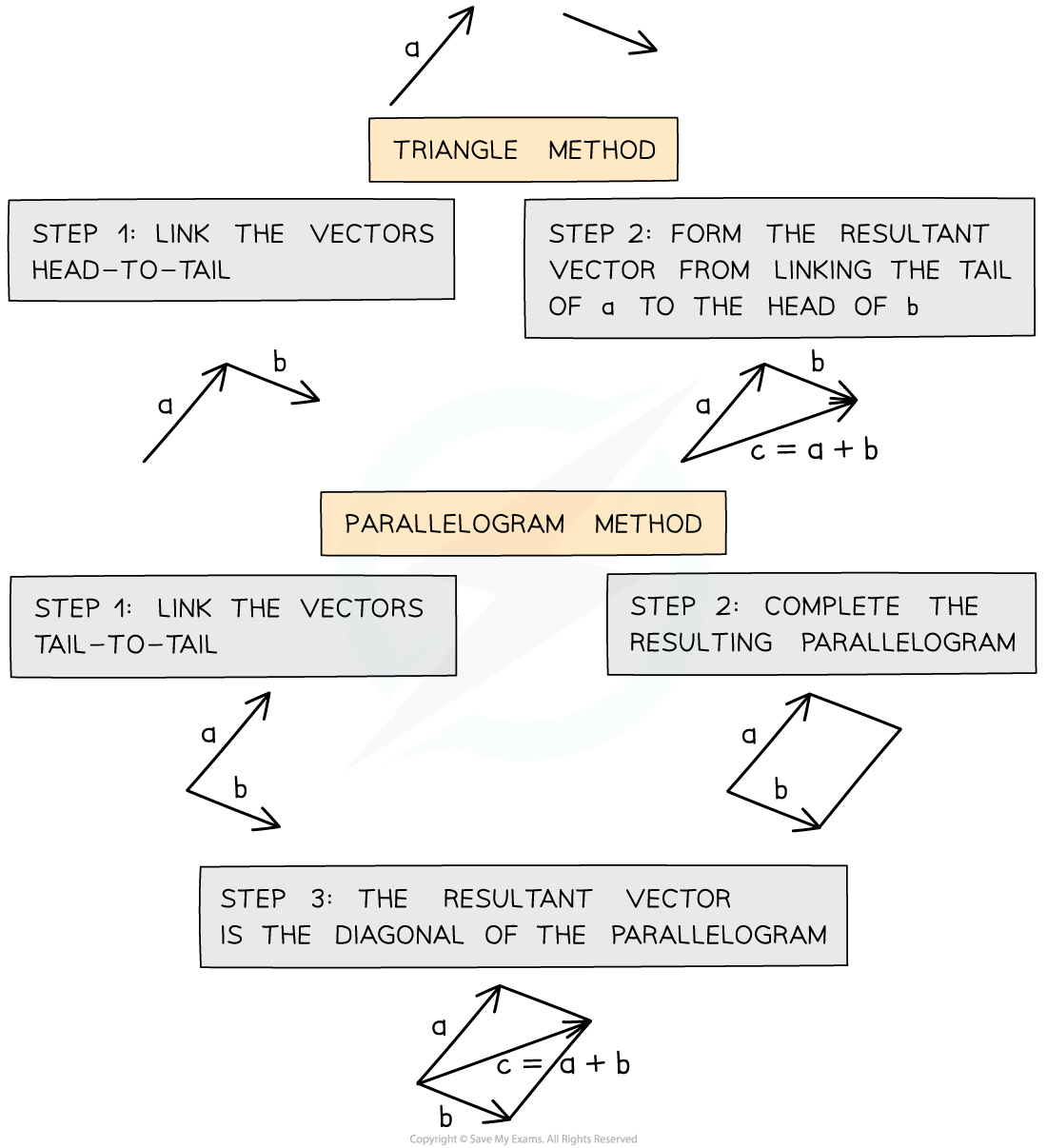
- There are two methods that can be used to combine vectors: the triangle method and the parallelogram method
- To combine vectors using the triangle method:
- Step 1: link the vectors head-to-tail
- Step 2: the resultant vector is formed by connecting the tail of the first vector to the head of the second vector
- To combine vectors using the parallelogram method:
- Step 1: link the vectors tail-to-tail
- Step 2: complete the resulting parallelogram
- Step 3: the resultant vector is the diagonal of the parallelogram
Worked Example
Draw the vector c = a + b
Worked Example
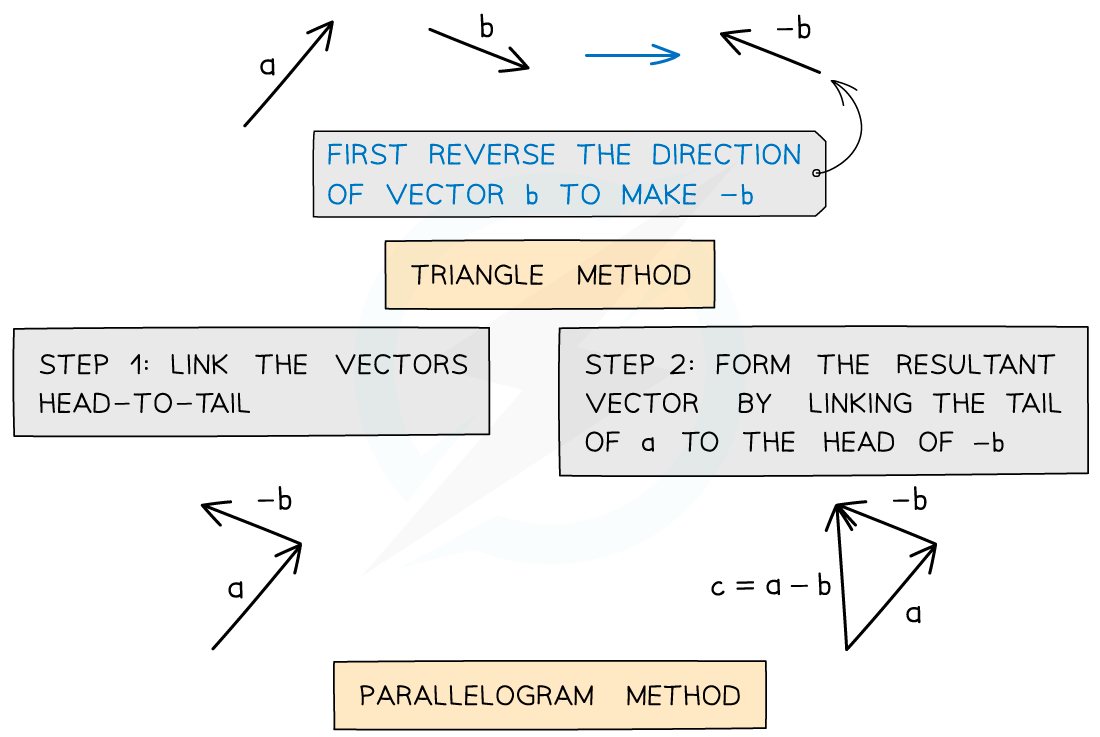
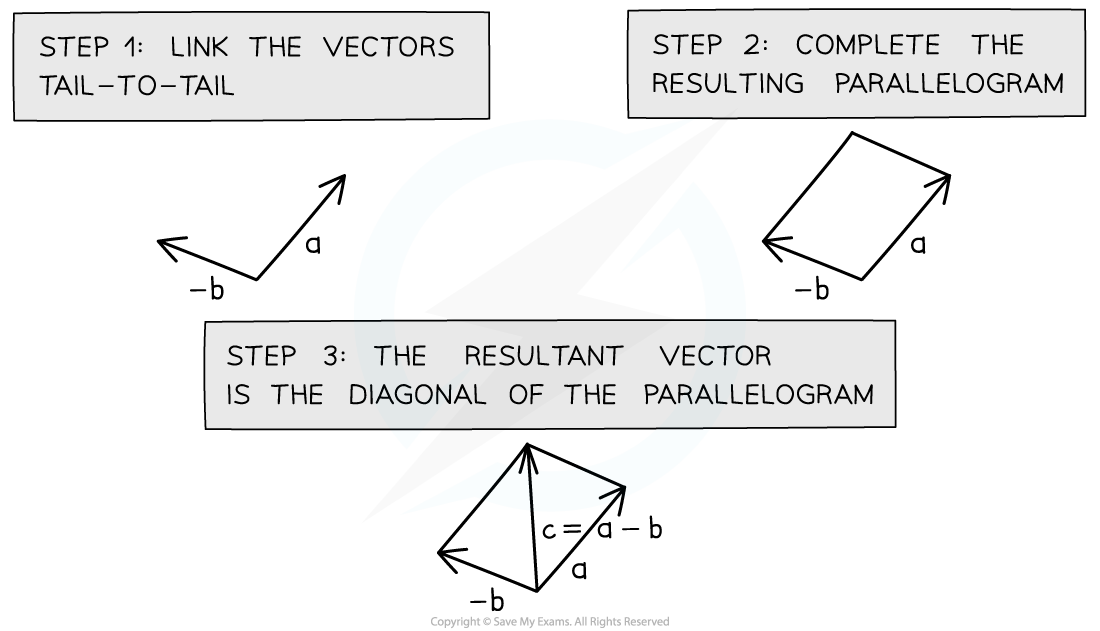
Draw the vector c = a – b
Resolving Vectors
- Two vectors can be represented by a single resultant vector
- Resolving a vector is the opposite of adding vectors
- A single resultant vector can be resolved
- This means it can be represented by two vectors, which in combination have the same effect as the original one
- When a single resultant vector is broken down into its parts, those parts are called components
- For example, a force vector of magnitude F and an angle of θ to the horizontal is shown below

The resultant force F at an angle θ to the horizontal
- It is possible to resolve this vector into its horizontal and vertical components using trigonometry

The resultant force F can be split into its horizontal and vertical components
- For the horizontal component, Fx = F cos θ
- For the vertical component, Fy = F sin θ
Worked Example
A hiker walks a distance of 6 km due east and 10 km due north.
Calculate the magnitude of their displacement and its direction from the horizontal.


Step 4: State the final answer complete with direction
R = 2√34 = 11.66 = 12 km
θ = 59° east and upwards from the horizontal
