AC Electrical Power Distribution
- Energy losses due to the heating of transmission lines in national power grids are significant
- This is because the electrical energy is transmitted across long distances from power stations to buildings
- Inefficiencies in a transformer appear not from just the core, but also in the wires
- The coils of wire have resistance
- This causes heat energy to be lost from the current flowing through the coils
- The larger the current, the greater the amount of heat energy lost
- In the core, the inefficiencies appear from:
- Induced eddy currents
- The reversal of magnetism
- Poor insulation between the primary and secondary coil
- Ways to reduce energy loss in a transformer are:
- Making the core from soft iron or iron alloys to allow easy magnetisation and demagnetisation and reduce hysteresis loss
- Laminating the core
- Using thick wires, especially in the secondary coil of step-down transformers
- Using a core that allows all the flux due to the primary coil to be linked to the secondary coil
- Power losses from the current are calculated using the equation:
P = I2R
- Where:
- P = power (W)
- I = current (A)
- R = resistance (Ω)
- The equation shows that:
- P ∝ I2
- This means doubling the current produces four times the power loss
- Therefore, step-up transformers are used to increase the voltage which decreases the current through transmission lines
- This reduces the overall heat energy lost in the wires during transmission
- A step-down transformer is then used to decrease the voltage to that required in homes and buildings
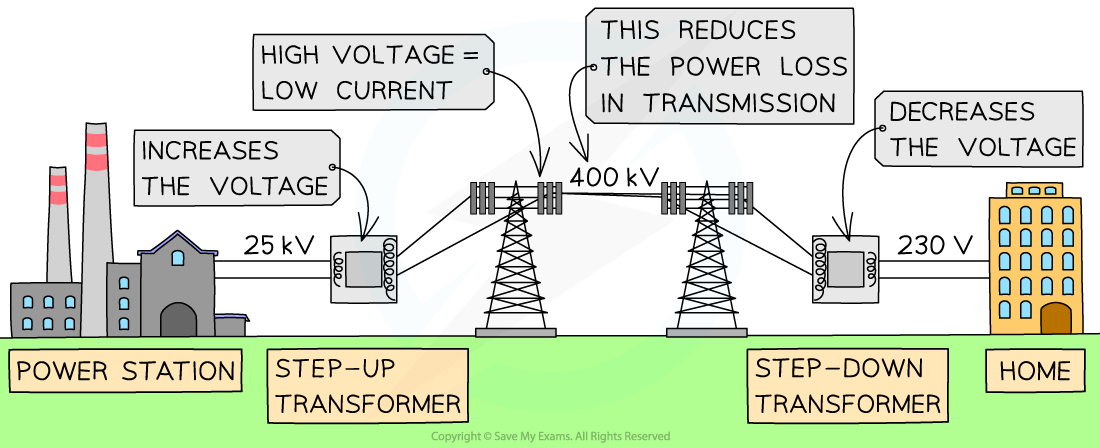
The use of step-up and step-down transformers in the National Grid
Worked Example
A current of 2500 A is transmitted through 150 km of cables. The resistance of the transmission cable is 0.15 Ω per km.
Calculate the power wasted.
Step 1: List the known quantities
- Current, I = 2500 A
- Length of cables, L = 150 km = 150 × 103 m
- Resistance of the cables, R = 0.15 Ω km-1
Step 2: Write out the power equation
P = I2R
Step 3: Determine the total resistance, R
R = Resistance of the wires × Length of wires
R = 0.15 × 150
Step 4: Substitute values into the power equation
Power lost = (2500)2 × (0.15 × 150) = 141 MW
