The Law of Radioactive Decay
- Since radioactive decay is spontaneous and random, it is useful to consider the average number of nuclei which are expected to decay per unit of time
- This is known as the average decay rate
- As a result, each radioactive element can be assigned a decay constant
- The decay constant λ is defined as:
The probability that an individual nucleus will decay per unit of time
- When a sample is highly radioactive, this means the number of decays per unit time is very high
- This suggests it has a high level of activity
- Activity, or the number of decays per unit time can be calculated using:
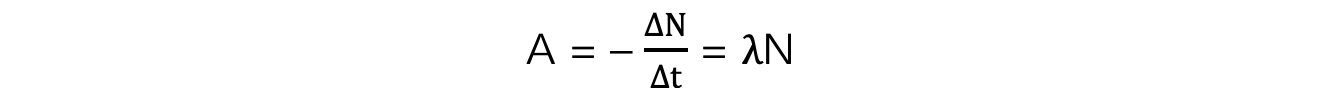
- Where:
- A = activity of the sample (Bq)
- ΔN = number of decayed nuclei
- Δt = time interval (s)
- λ = decay constant (s-1)
- N = number of nuclei remaining in a sample
- In radioactive decay, the number of undecayed nuclei falls very rapidly, without ever reaching zero
- Such a model is known as exponential decay
- The graph of number of undecayed nuclei against time has a very distinctive shape:
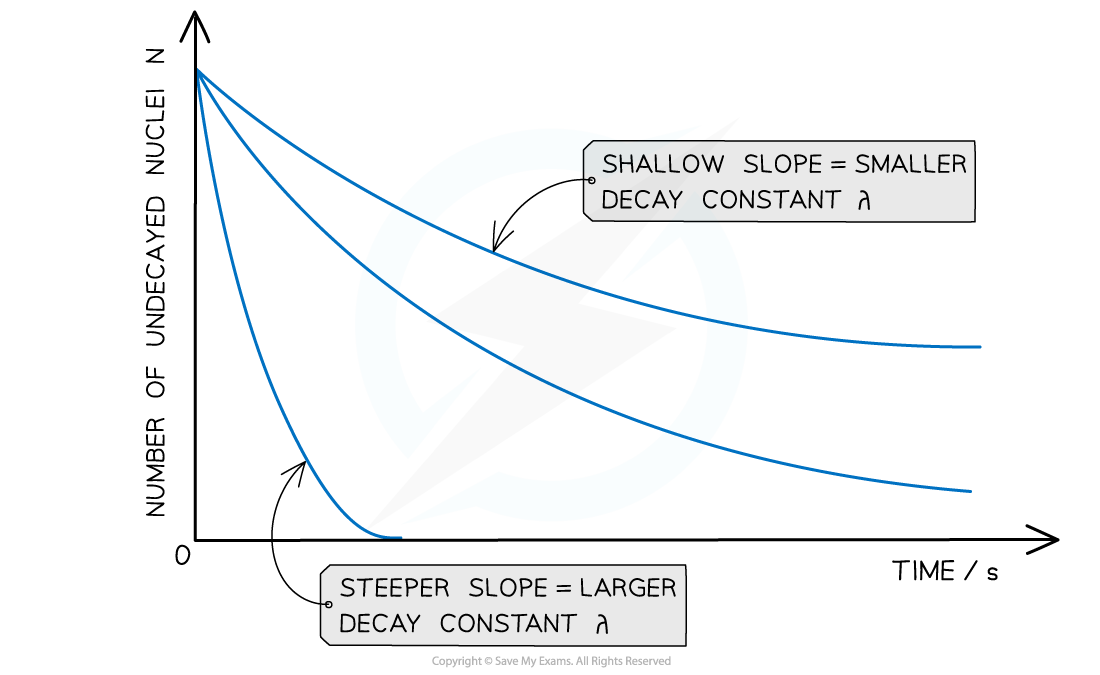
Radioactive decay follows an exponential pattern. The graph shows three different isotopes each with a different rate of decay
- The key features of this graph are:
- The steeper the slope, the larger the decay constant λ (and vice versa)
- The decay curves always start on the y-axis at the initial number of undecayed nuclei (N0)
- The law of radioactive decay states:
The rate of decay of a nuclide is proportional to the amount of radioactive material remaining
- The number of undecayed nuclei N can be represented in exponential form by the equation:
N = N0 e–λt
- Where:
- N0 = the initial number of undecayed nuclei (when t = 0)
- N = number of undecayed nuclei at a certain time t
- λ = decay constant (s-1)
- t = time interval (s)
- The number of nuclei can be substituted for other quantities
- For example, the activity A is directly proportional to N, so it can also be represented in exponential form by the equation:
A = A0 e–λt
- Where:
- A = activity at a certain time t (Bq)
- A0 = initial activity (Bq)
- The received count rate C is related to the activity of the sample, hence it can also be represented in exponential form by the equation:
C = C0 e–λt
- Where:
- C = count rate at a certain time t (counts per minute or cpm)
- C0 = initial count rate (counts per minute or cpm)
Exam Tip
The symbol e represents the exponential constant - it is approximately equal to e = 2.718
On a calculator, it is shown by the button ex
The inverse function of ex is ln(y), known as the natural logarithmic function - this is because, if ex = y, then x = ln(y)
Make sure you are confident using the exponential and natural logarithmic functions, they are a major component of the mathematics in this topic!
Problems Involving the Radioactive Decay Law
Worked Example
Strontium-90 decays with the emission of a β-particle to form Yttrium-90. The decay constant of Strontium-90 is 0.025 year -1.
Determine the activity A of the sample after 5.0 years, expressing the answer as a fraction of the initial activity A0.
Step 1: Write out the known quantities
-
- Decay constant, λ = 0.025 year -1
- Time interval, t = 5.0 years
- Both quantities have the same unit, so there is no need for conversion
Step 2: Write the equation for activity in exponential form
A = A0 e–λt
Step 3: Rearrange the equation for the ratio between A and A0
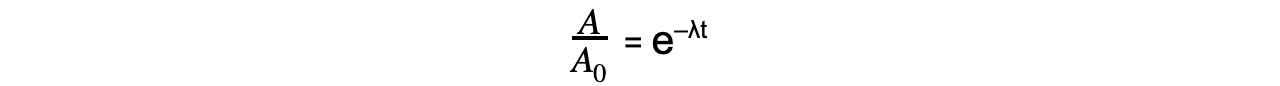
Step 4: Calculate the ratio A/A0
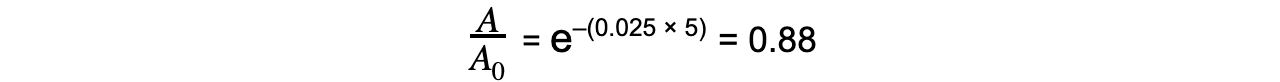
-
- Therefore, the activity of Strontium-90 decreases by a factor of 0.88, or 12%, after 5 years
Worked Example
Americium-241 is an artificially produced radioactive element that emits α-particles.
In a smoke detector, a sample of americium-241 of mass 5.1 µg is found to have an activity of 5.9 × 105 Bq. The supplier’s website says the americium-241 in their smoke detectors initially has an activity level of 6.1 × 105 Bq.
Part (a)
Step 1: Write down the known quantities
-
-
- Mass = 5.1 μg = 5.1 × 10-6 g
- Molecular mass of americium = 241
- NA = the Avogadro constant
-
Step 2: Write down the equation relating to the number of nuclei, mass and molecular mass
Step 3: Calculate the number of nuclei
Part (b)
Step 1: Write down the known quantities
-
-
- Activity, A = 5.9 × 105 Bq
- Number of nuclei, N = 1.27 × 1016
-
Step 2: Write the equation for activity
Activity, A = λN
Step 3: Rearrange for decay constant λ and calculate the answer
Part (c)
Step 1: Write down the known quantities
-
-
- Activity, A = 5.9 × 105 Bq
- Initial activity, A0 = 6.1 × 105 Bq
- Decay constant, λ = 4.65 × 10–11 s–1
-
Step 2: Write the equation for activity in exponential form
A = A0 e–λt
Step 3: Rearrange for time t
Step 4: Calculate the age of the smoke detector and convert to years
-
-
- Therefore, the smoke detector is 22.7 years old
-
