9.3.1 Young’s Double-Slit Experiment

• Young’s double-slit experiment demonstrates how light waves can produce an interference pattern
• The setup of the experiment is shown below:

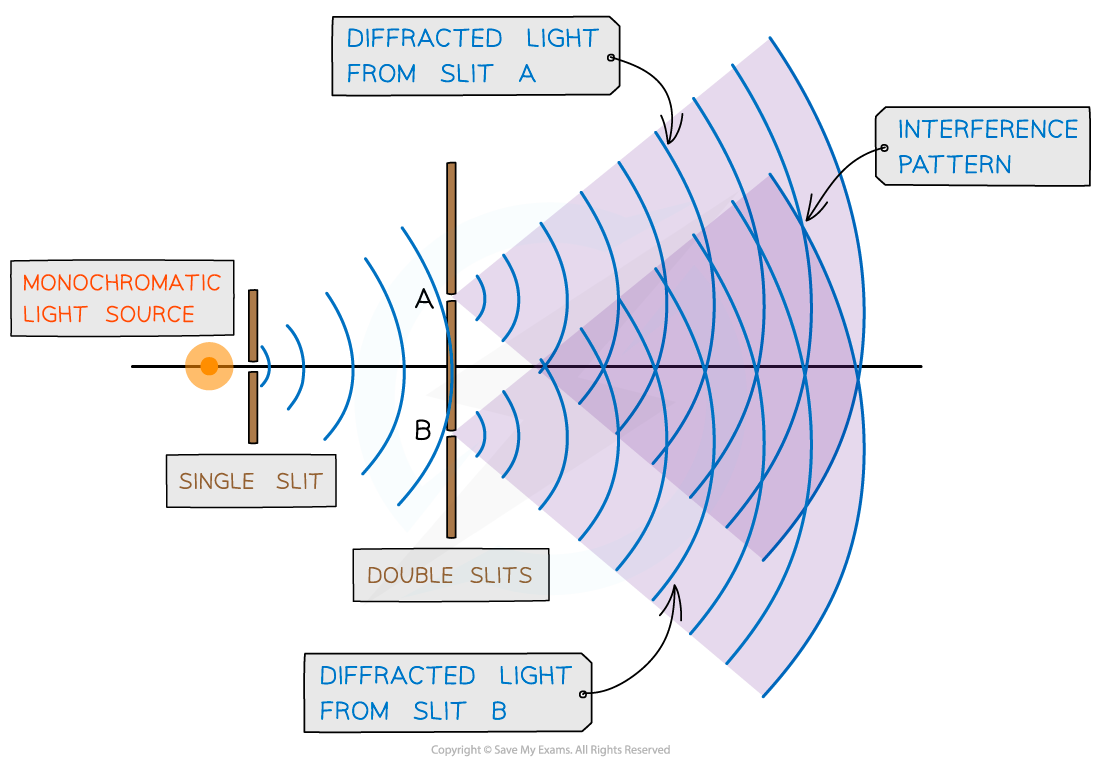
Young’s double-slit experiment arrangement

• When a monochromatic light source is placed behind a single slit, the light is diffracted producing two light sources at the double slits A and B
• Since both light sources originate from the same primary source, they are coherent and will therefore create an observable interference pattern
  • Both diffracted light from the double slits create an interference pattern made up of bright and dark fringes
• The distance between the fringes can be calculated using the double-slit equation:

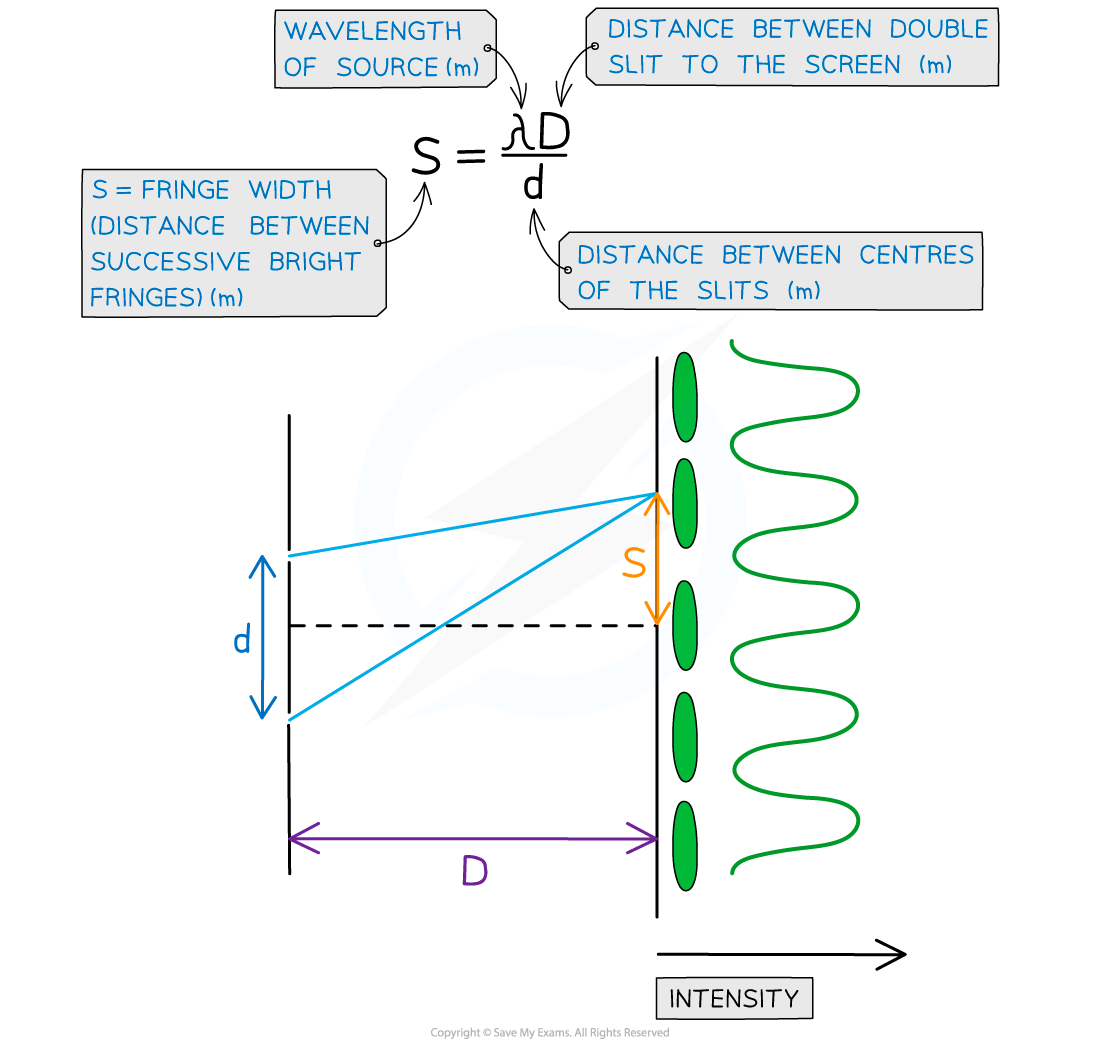
Double slit interference equation with d, s and D represented on a diagram

Investigating Young’s Double-Slits Experimentally

The overall aim of this experiment is to investigate the relationship between the distance between the slits and the screen, D, and the fringe width, s

• Independent variable = Fringe width, s
• Dependent variable = Distance between the slits and the screen, D
• Control variables
  • Laser wavelength, λ
  • Slit separation, d

Method

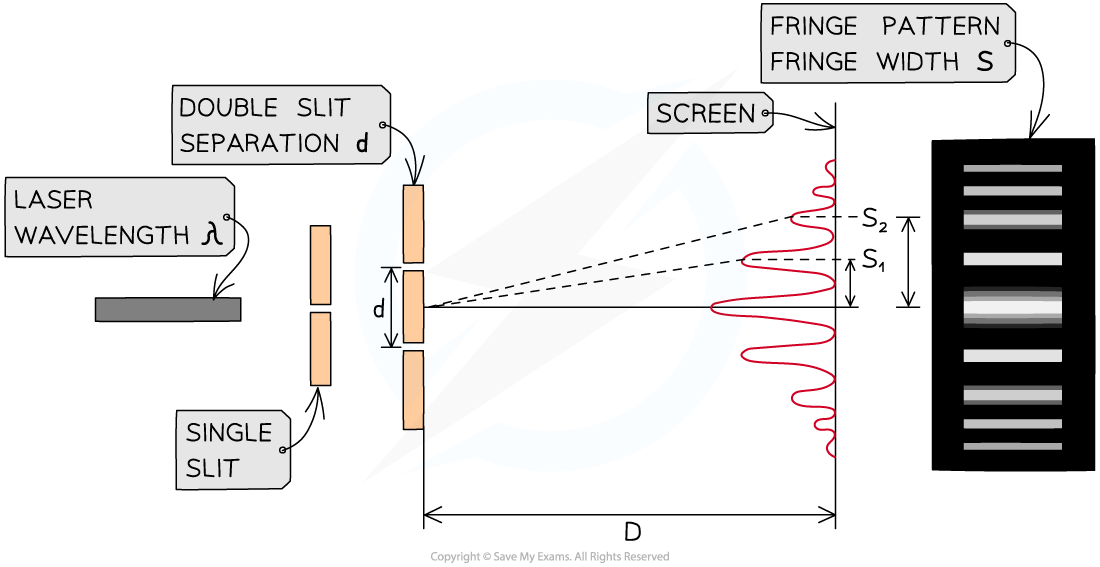
The setup of apparatus required to measure the fringe width s for different values of D

1. Set up the apparatus by fixing the laser and the slits to a retort stand and place the screen so that D is 0.5 m, measured using the metre ruler
2. Darken the room and turn on the laser
3. Measure from the central fringe across many fringes using the vernier callipers (or ideally, a travelling microscope) and divide by the number of fringe widths to find the fringe width, s
4. Increase the distance D by 0.1 m and repeat the procedure, increasing it by 0.1 m each time up to around 1.5 m
5. Repeat the experiment twice more and calculate and record the mean fringe width, s, for each distance D

• An example table might look like this:

Analysing the Results

• The fringe spacing equation is given by:

• Where:
  • s = the distance between each fringe (m)
  • λ = the wavelength of the laser light (m)
  • D = the distance between the slit and the screen (m)
  • d = the slit separation (m)

• Comparing this to the equation of a straight line: y = mx
  • y = s (m)
  • x = D (m)
  • Gradient =  (unitless)

• Plot a graph of s against D and draw a line of best fit
• The wavelength of the laser light is equal to the gradient multiplied by the slit separation, as shown by the graph:

Evaluating the Experiment

Systematic errors:

• Ensure the use of the set square to avoid parallax error in the measurement of the fringe width
• The distance between fringes is very small due to the short wavelength of visible light
  • A monochromatic light source must be used so that the fringes easier to observe

Random errors:

• The fringe spacing can be subjective depending on its intensity on the screen, therefore, take multiple measurements of s (between 3-8) and find the average
• Use a Vernier scale to record distances s to reduce percentage uncertainty
  • Use a travelling microscope, if available, for the greatest accuracy
• Reduce the uncertainty in s by measuring across all visible fringes and dividing by the number of fringes
• Conduct the experiment in a darkened room, so the fringes are clear

Safety Considerations

• Lasers should be Class 2 and have a maximum output of no more than 1 mW
• Do not allow laser beams to shine into anyone’s eyes
• Remove reflective surfaces from the room to ensure no laser light is reflected into anyone’s eyes