6.2.3 Gravitational Field Strength

• There is a universal force of attraction between all matter with mass
  • This force is known as the ‘force due to gravity’ or the weight

• The Earth’s gravitational field is responsible for the weight of all objects on Earth
• A gravitational field is defined as:

A region of space where a test mass experiences a force due to the gravitational attraction of another mass

•  The direction of the gravitational field is always towards the centre of the mass causing the field
  • Gravitational forces cannot be repulsive

• Gravity has an infinite range, meaning it affects all objects in the universe
  • There is a greater gravitational force around objects with a large mass (such as planets)
  • There is a smaller gravitational force around objects with a small mass (almost negligible for atoms)

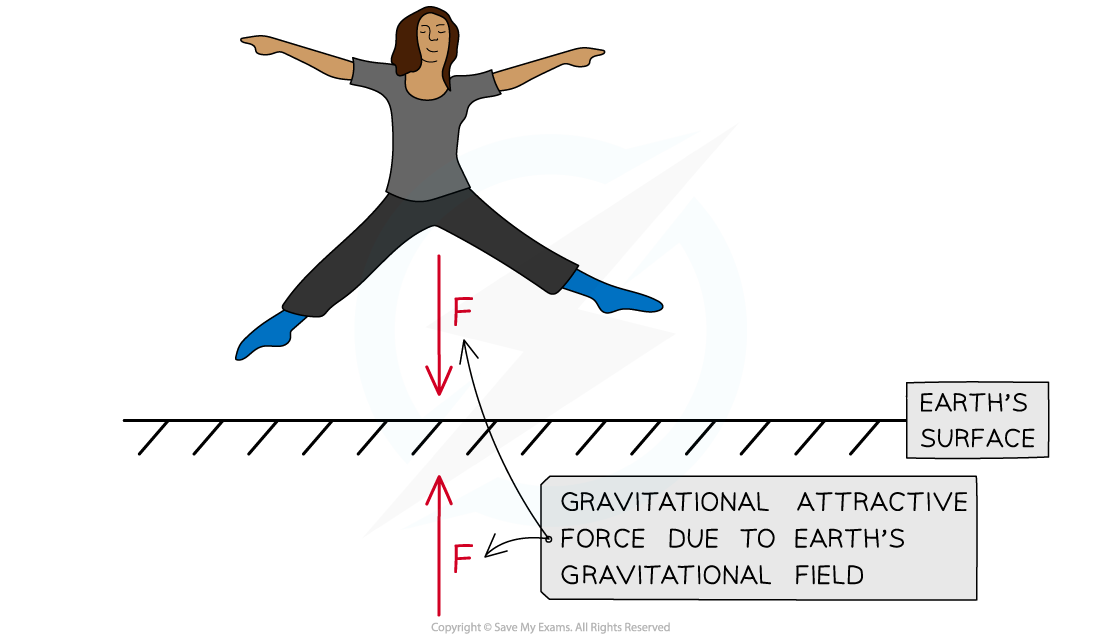
The Earth's gravitational field produces an attractive force. The force of gravity is always attractive

• The gravitational field strength at a point is defined as:

The force per unit mass experienced by a test mass at that point

• This can be written in equation form as:

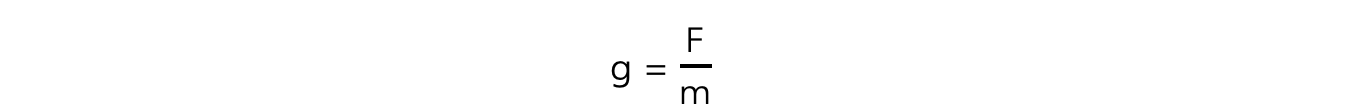
• Where:
  • g = gravitational field strength (N kg⁻¹)
  • F = force due to gravity, or weight (N)
  • m = mass of test mass in the field (kg)

• This equation shows that:
  • On planets with a large value of g, the gravitational force per unit mass is greater than on planets with a smaller value of g

• An object's mass remains the same at all points in space
  • However, on planets such as Jupiter, the weight of an object will be greater than on a less massive planet, such as Earth
  • This means the gravitational force would be so high that humans, for example, would not be unable to fully stand up

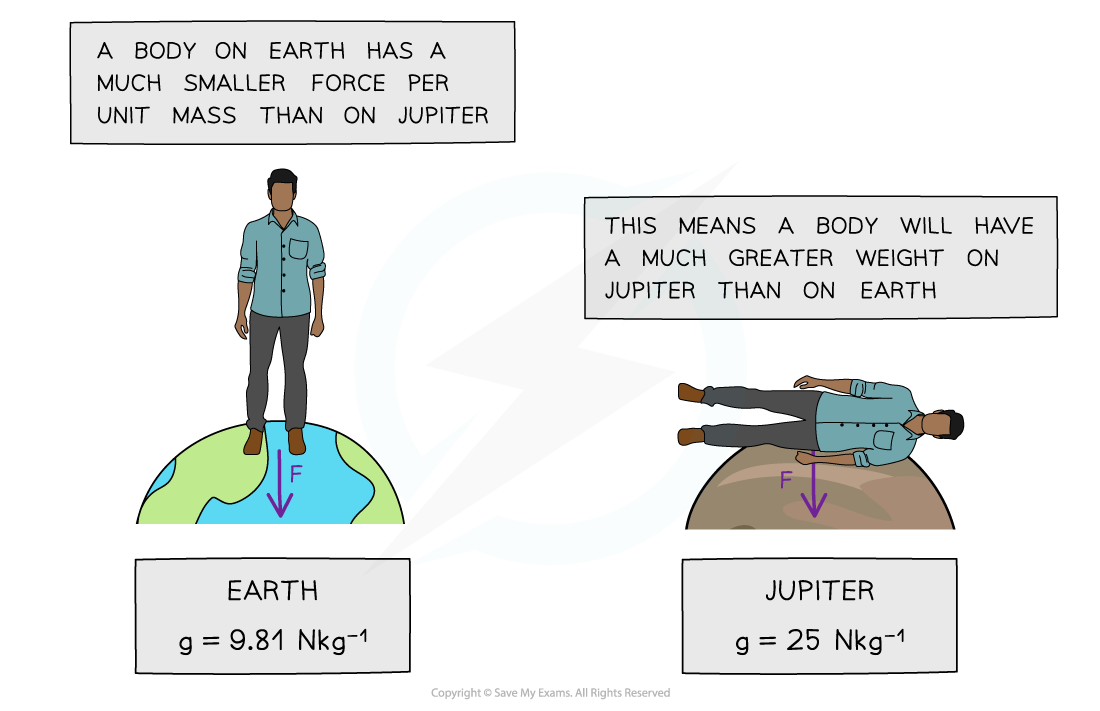
A person’s weight on Jupiter would be so large that a human would be unable to fully stand up

• Factors that affect the gravitational field strength at the surface of a planet are:
  • The radius r (or diameter) of the planet
  • The mass M (or density) of the planet

• This can be shown by equating the equation F = mg with Newton's law of gravitation:

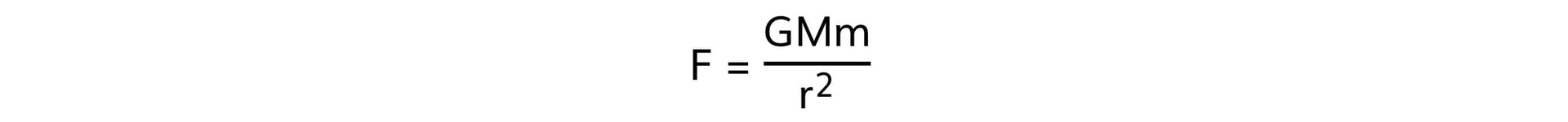
• Substituting the force F with the gravitational force mg leads to:

• Cancelling the mass of the test mass, m, leads to the equation:

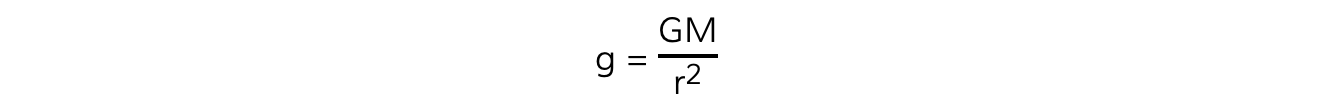
• Where:
  • G = Newton's Gravitational Constant
  • M = mass of the body causing the field (kg)
  • r = distance from the mass where you are calculating the field strength (m)

• This equation shows that: 
  • The gravitational field strength g depends only on the mass of the body M causing the field
  • Hence, objects with any mass m in that field will experience the same gravitational field strength
  • The gravitational field strength g is inversely proportional to the square of the radial distance, r²

• In a similar way to other vectors, such as force or velocity, the gravitational field strength due to two bodies can be determined
  • This is because gravitational field strength is a vector, meaning it has both a magnitude and direction

• The resultant gravitational field strength is, therefore, the vector sum of the gravitational field strength due to each body

Step 1: List the known quantities

• • Mass of one star, M = 5.0 × 10³⁰ kg
  • Distance between one star and the planet, r = 3.0 × 10¹² m
  • Angle between the gravitational field strength and the planet, θ = 42°

Step 2: Write out the equation for gravitational field strength

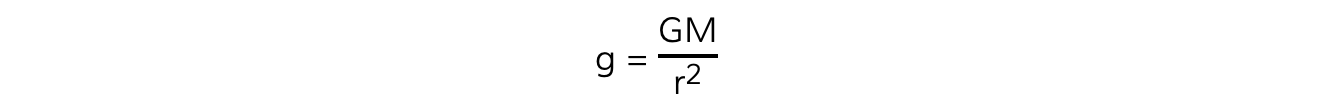
Step 3: Calculate the gravitational field strength due to one star 

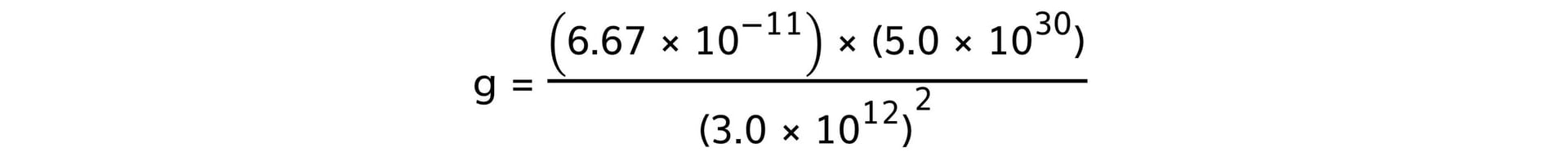
g = 3.7 × 10⁻⁵ N kg⁻¹

Step 4: Resolve the vectors vertically

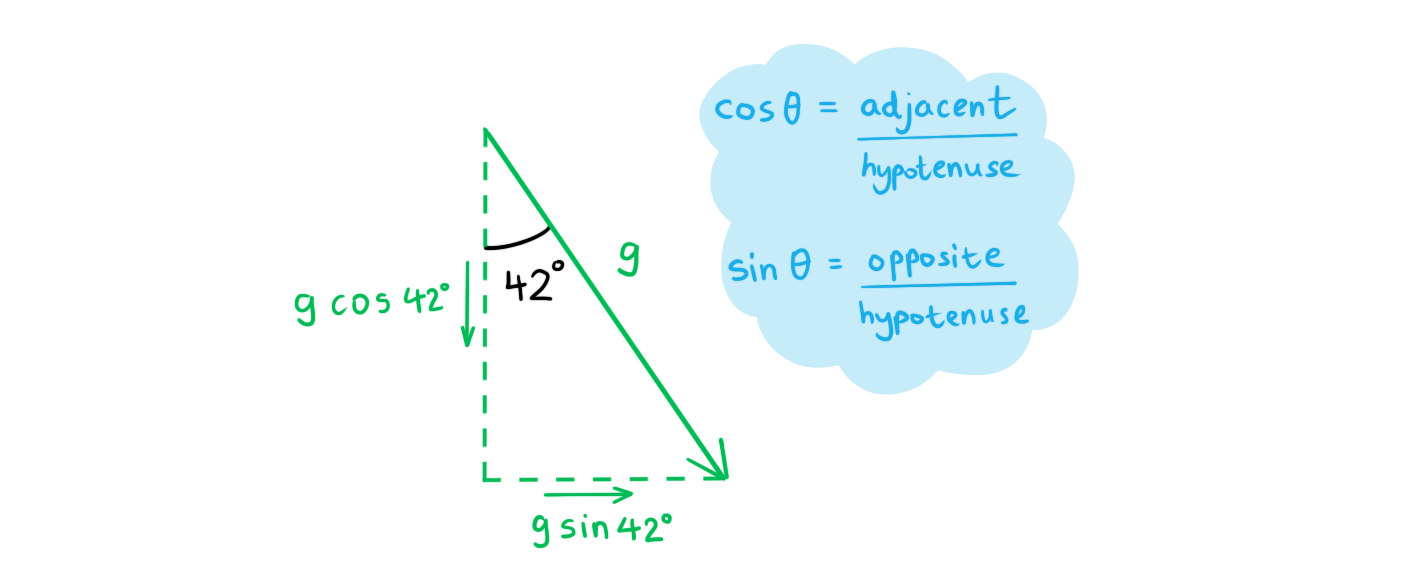
• • The vertical component of each vector is g cos 42°

Step 5: Use vector addition to determine the resultant gravitational field strength

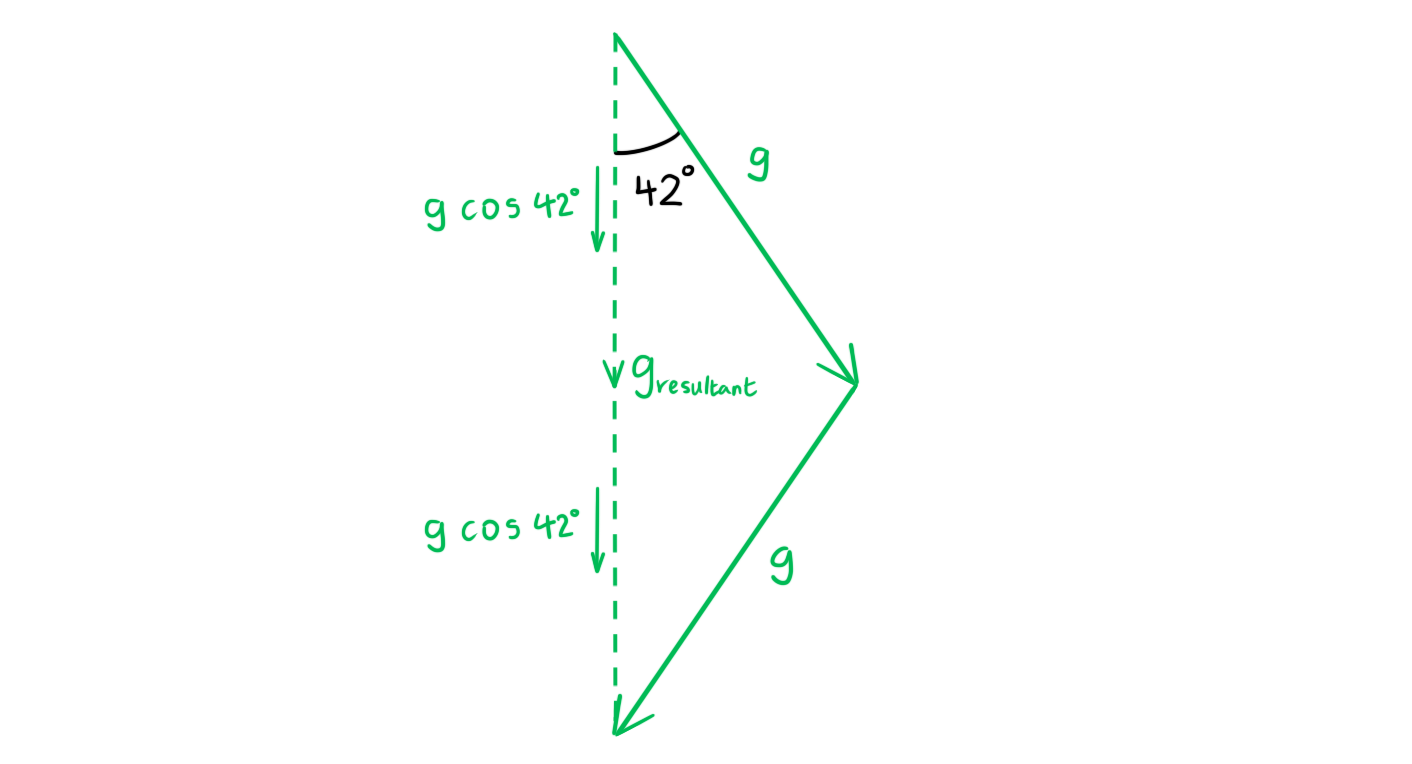
g_resultant = g cos 42° + g cos 42° = 2g cos 42°

g_resultant = 2 × (3.7 × 10⁻⁵) × cos 42°

g_resultant = 5.5 × 10⁻⁵ N kg⁻¹