4.2.4 Sound Waves

• Sound waves are longitudinal waves and, as such, require a medium in which to propagate
• Sound waves are generated by oscillating sources, which produce a change in density of the surrounding medium
• The sound wave then travels with a series of compressions and rarefactions

A sound wave travelling through air

• Sound waves form a continuous spectrum based on their frequency

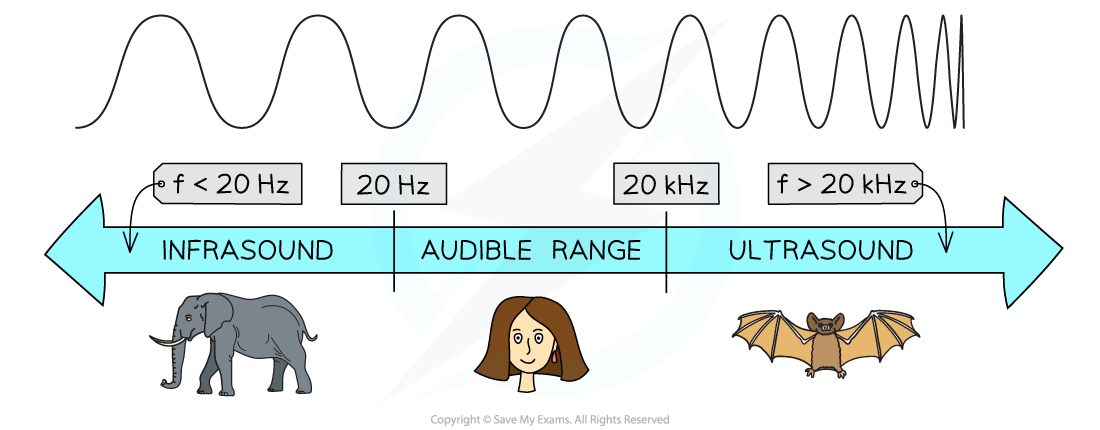
The spectrum of sound waves

• Humans can only hear sounds with frequencies in the range 20 Hz - 20 kHz, known as the audible range 
• Sounds with frequencies below and above this range cannot be detected by the human ear

Pitch and Volume

• The frequency of a sound wave is related to its pitch
  • Sounds with a high pitch have a high frequency (or short wavelength)
  • Sounds with a low pitch have a low frequency (or long wavelength)

• The amplitude of a sound wave is related to its volume
  • Sounds with a large amplitude have a high volume
  • Sounds with a small amplitude have a low volume

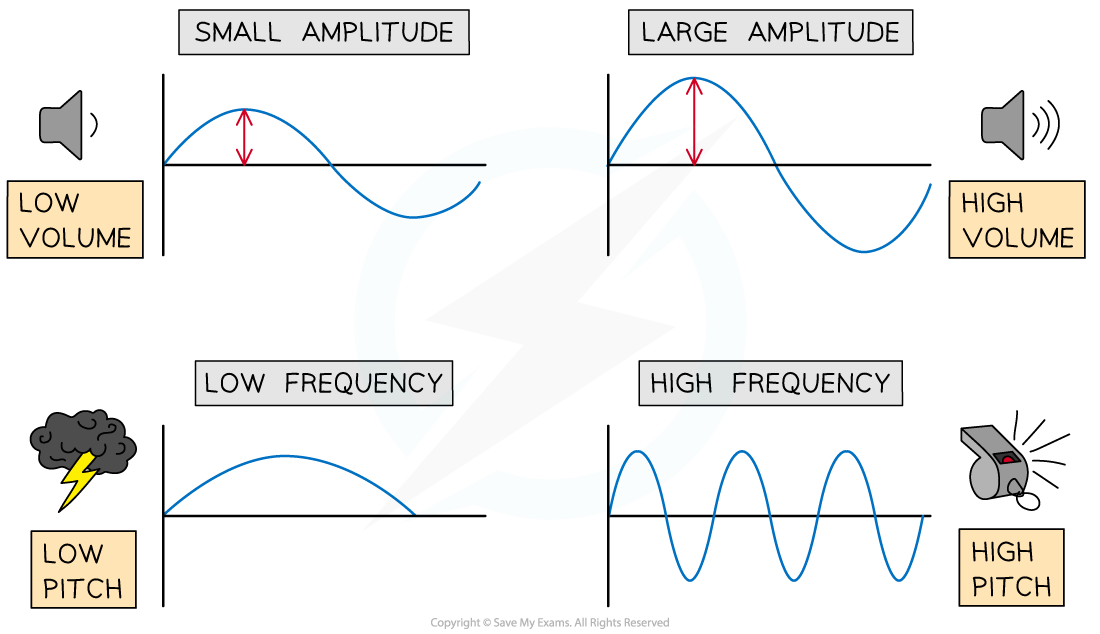
Pitch and amplitude of sound

Speed of Sound

• Sound waves travel at a speed of about 340 m s^–1 in air at room temperature
  • The higher the air temperature, the greater the speed of sound
  • The is because the average kinetic energy of the particles is higher

• Sound travels the fastest through solids, since solid particles are closely packed and can pass the oscillations onto their neighbours much faster
• Sound travels the slowest in gases, since gas particles are spread out and less efficient in transferring the oscillations to their neighbours

Echo

• Sound waves reflect off hard surfaces
• This phenomenon is known as echo
• Echo can be used to obtain an experimental value of the speed of sound. This is calculated using the equation

• Where:
  • v = speed of sound in metres per second (m s^–1)
  • d = distance between the sound source and the hard surface (m)
  • t = time taken to travel from the source to the hard surface and back (s)

Measuring the Speed of Sound Experimentally - Fast Timer

• The speed of sound can be measured using a fast timer (one which can measure to the nearest millisecond or even microsecond)
• Two microphones separated 1 m apart are connected to a fast timer
  • The first microphone triggers the timer to start
  • The second microphone triggers the timer to stop

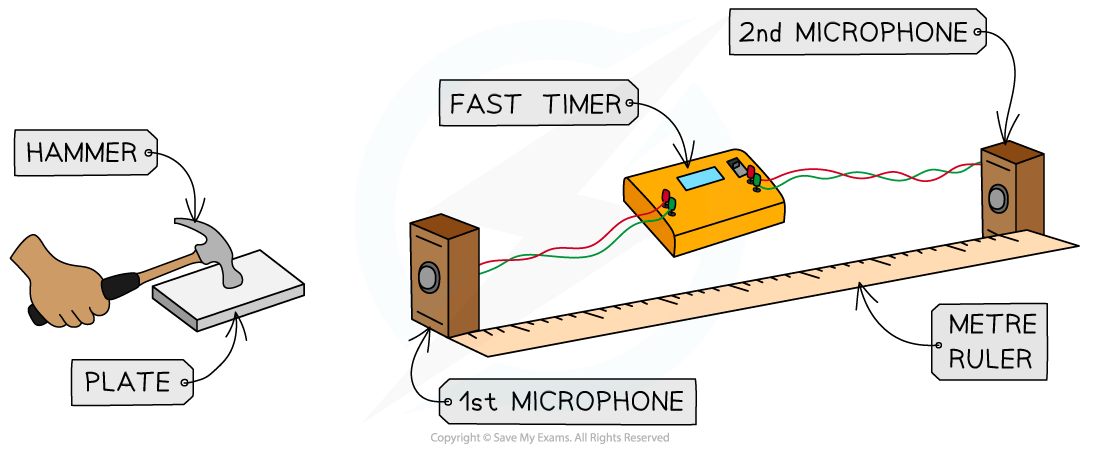
• A hammer is made to strike a plate
• The sound waves from the plate travel to the two microphones triggering the first and then the second
  • The time delay will be around 3.2 ms

• The speed of the waves can be calculated by rearranging the equation: distance = speed × time

Measuring the Speed of Sound Experimentally - Double Beam Oscilloscope

• Two microphones are connected to the input of a double beam oscilloscope
• A signal generator is connected to a loudspeaker and set to a frequency between 500 Hz and 2.0 kHz
  • One of the microphones is close to the loud speaker
  • The other microphone is 1 m away

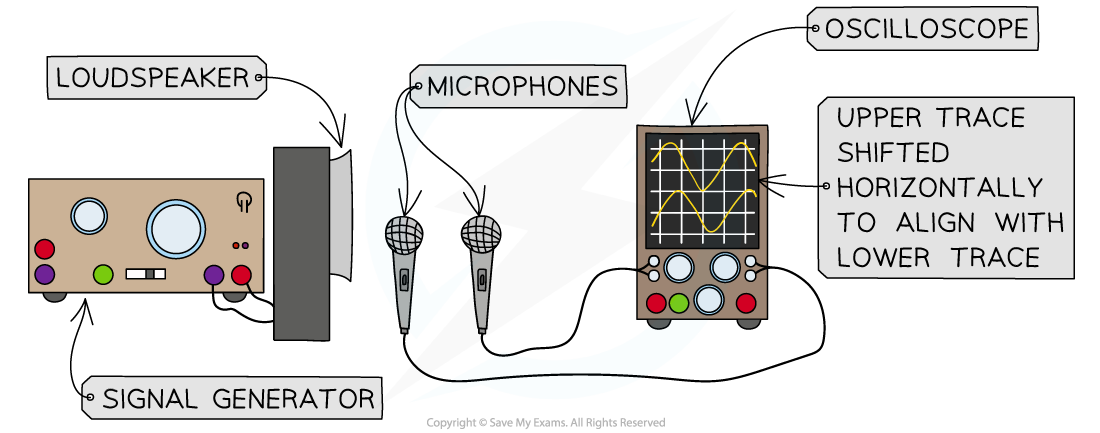
• There will be two traces that appear on the screen
• The traces are compared as the second microphone is moved back and forth in line with the first microphone and the speaker
• Use a ruler to measure the distance that the second microphone needs to move for the traces to be in phase then out and phase and back in phase again
  • This distance is equal to the wavelength of the wave

• The speed of the waves are therefore calculated using c = fλ

Step 1: Write down the known quantities

• • Distance between the person and the wall, d = 50 m
  • Time between the claps, t = 0.30 s

Step 2: Write down the "echo equation" 

Step 3: Substitute the numbers into the above equation and calculate the speed of sound v 

v = 330 m s^–1