| Date | May 2016 | Marks available | 4 | Reference code | 16M.3ca.hl.TZ0.5 |
| Level | HL only | Paper | Paper 3 Calculus | Time zone | TZ0 |
| Command term | Show that | Question number | 5 | Adapted from | N/A |
Question
Consider the infinite series \(S = \sum\limits_{n = 0}^\infty {{u_n}} \) where \({u_n} = \int_{nx}^{(n + 1)\pi } {\frac{{\sin t}}{t}{\text{d}}t} \).
Explain why the series is alternating.
(i) Use the substitution \(T = t - \pi \) in the expression for \({u_{n + 1}}\) to show that \(\left| {{u_{n + 1}}} \right| < \left| {{u_n}} \right|\).
(ii) Show that the series is convergent.
Show that \(S < 1.65\).
Markscheme
as \(t\) moves through the intervals \([0,{\text{ }}\pi ],{\text{ }}[\pi ,{\text{ }}2\pi ],{\text{ }}[2\pi ,{\text{ }}3\pi ],{\text{ }}[3\pi ,{\text{ }}4\pi ]\), etc, the sign of \(\sin t\), (and therefore the sign of the integral) alternates \( + ,{\text{ }} - ,{\text{ }} + ,{\text{ }} - \), etc, so that the series is alternating R1
Note: Award R1 only if it includes a clear reason that justifies that the sign of the integrand alternates between − and + and this pattern is valid for all the terms.
The change of signs can be justified by a labelled graph of \(y = \sin (x)\) or \(y = \frac{{\sin x}}{x}\) that shows the intervals \([0,{\text{ }}\pi ],{\text{ }}[\pi ,{\text{ }}2\pi ],{\text{ }}[2\pi ,{\text{ }}3\pi ],{\text{ }} \ldots \)
[1 mark]
(i) \({u_{n + 1}} = \int_{(n + 1)\pi }^{(n + 2)\pi } {\frac{{\sin t}}{t}{\text{d}}t} \)
(M1)
put \(T = t--\pi \) and \({\text{d}}T = {\text{d}}t\) (M1)
the limits change to \(n\pi ,{\text{ }}(n + 1)\pi \)
\(\left| {{u_{n + 1}}} \right| = \int_{n\pi }^{(n + 1)\pi } {\frac{{\left| {\sin (T + \pi )} \right|}}{{T + \pi }}{\text{d}}T} \) (or equivalent) A1
\(\left| {\sin (T + \pi )} \right| = \left| {\sin (T)} \right|\) or \(\sin (T + \pi ) = - \sin (T)\) (M1)
\( = \int_{n\pi }^{(n + 1)\pi } {\frac{{\left| {\sin T} \right|}}{{T + \pi }}{\text{d}}T} \)
\( < \int_{n\pi }^{(n + 1)\pi } {\frac{{\left| {\sin T} \right|}}{T}{\text{d}}T = \left| {{u_n}} \right|} \) A1AG
(ii) \(\left| {{u_n}} \right| = \int_{n\pi }^{(n + 1)\pi } {\frac{{\sin t}}{t}{\text{d}}t} \)
\( < \int_{n\pi }^{(n + 1)\pi } {\frac{1}{t}{\text{d}}t} \) M1
\( = [\ln t]_{n\pi }^{(n + 1)\pi }\) A1
\( = \ln \left( {\frac{{n + 1}}{n}} \right)\) A1
\( \to \ln 1 = 0\) as \(n \to \infty \)
from part (i) \(\left| {{u_n}} \right|\) is a decreasing sequence and since \(\mathop {\lim }\limits_{n \to \infty } \left| {{u_n}} \right| = 0\), R1
the series is convergent AG
[9 marks]
attempt to calculate the partial sums \(\sum\limits_{i = 0}^{n - 1} {{u_i} = \int_0^{n\pi } {\frac{{\sin t}}{t}{\text{d}}t} } \) (M1)
the first partial sums are
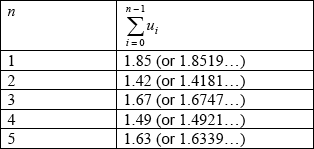
two consecutive partial sums for \(n \geqslant 4\) A1A1
(eg \({S_4} = 1.49\) and \({S_5} = 1.63\) or \({S_{100}} = 1.567 \ldots \) and \({S_{101}} = 1.573 \ldots \))
Note: These answers must be given to a minimum of 3 significant figures.
the sum to infinity lies between any two consecutive partial sums,
eg between 1.49 and 1.63 R1
so that \(S < 1.65\) AG
Note: Award A1A1R1 to candidates who calculate at least two partial sums for only odd values of \(n\) and state that the upper bound is less than these values.
[4 marks]
Examiners report
Very few candidates presented a valid reason to justify the alternating nature of the series. In most cases candidates just reformulated the wording of the question by saying that it changed signs and completely ignored the interval over which the expression had to be integrated to obtain each term.
(i) Most candidates achieved 1 or 2 marks for attempting the given substitution; in most cases candidates failed to find the correct limits of integration for the new variable and then relate the expressions of the consecutive terms of the series. In part (ii) very few correct attempts were seen; in some cases candidates did recognize the conditions for the alternating series to be convergent but very few got close to establish that the limit of the general term was zero.
A few good attempts to use partial sums were seen although once again candidates showed difficulties in identifying what was needed to show the given answer. In most cases candidates just verified with GDC that in fact for high values of n the series was indeed less than the upper bound given but could not provide a valid argument that justified the given statement.

