| Date | November 2013 | Marks available | 9 | Reference code | 13N.3ca.hl.TZ0.5 |
| Level | HL only | Paper | Paper 3 Calculus | Time zone | TZ0 |
| Command term | Justify, Sketch, State, and Write down | Question number | 5 | Adapted from | N/A |
Question
A function \(f\) is defined in the interval \(\left] { - k,{\text{ }}k} \right[\), where \(k > 0\). The gradient function \({f'}\) exists at each point of the domain of \(f\).
The following diagram shows the graph of \(y = f(x)\), its asymptotes and its vertical symmetry axis.
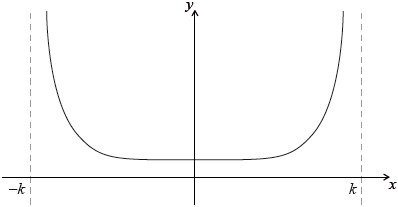
(a) Sketch the graph of \(y = f'(x)\).
Let \(p(x) = a + bx + c{x^2} + d{x^3} + \ldots \) be the Maclaurin expansion of \(f(x)\).
(b) (i) Justify that \(a > 0\).
(ii) Write down a condition for the largest set of possible values for each of the parameters \(b\), \(c\) and \(d\).
(c) State, with a reason, an upper bound for the radius of convergence.
Markscheme
(a)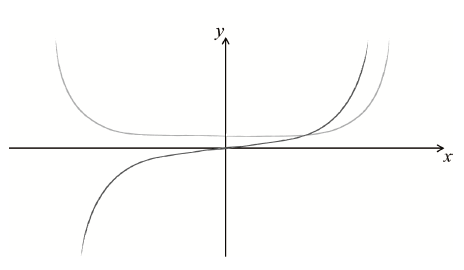
A1 for shape, A1 for passing through origin A1A1
Note: Asymptotes not required.
[2 marks]
(b) \(p(x) = \underbrace {f(0)}_a + \underbrace {f'(0)}_bx + \underbrace {\frac{{f''(0)}}{{2!}}}_c{x^2} + \underbrace {\frac{{{f^{(3)}}(0)}}{{3!}}}_d{x^3} + \ldots \)
(i) because the y-intercept of \(f\) is positive R1
(ii) \(b = 0\) A1
\(c \geqslant 0\) A1A1
Note: A1 for \( > \) and A1 for \( = \).
\(d = 0\) A1
[5 marks]
(c) as the graph has vertical asymptotes \(x = \pm k,{\text{ }}k > 0\), R1
the radius of convergence has an upper bound of \(k\) A1
Note: Accept \(r < k\).
[2 marks]
Examiners report
Overall candidates made good attempts to parts (a) and most candidates realized that the graph contained the origin; however many candidates had difficulty rendering the correct shape of the graph of \(f'\). Part b(i) was also well answered although some candidates where not very clear and digressed a lot. Part (ii) was less successful with most candidates scoring just part of the marks. A small number of candidates answered part (c) correctly with a valid reason.

