| Date | May 2013 | Marks available | 5 | Reference code | 13M.3ca.hl.TZ0.5 |
| Level | HL only | Paper | Paper 3 Calculus | Time zone | TZ0 |
| Command term | Find, Hence, and Show that | Question number | 5 | Adapted from | N/A |
Question
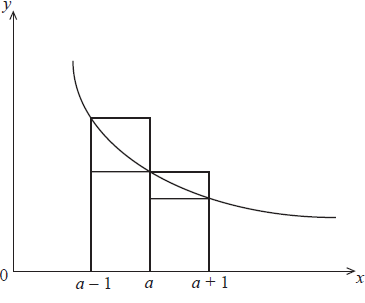
Figure 1
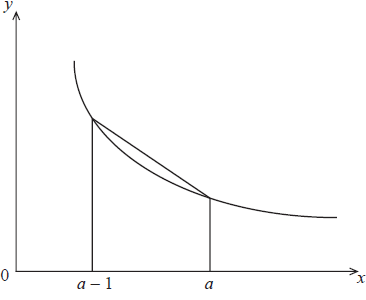
Figure 2
Figure 1 shows part of the graph of \(y = \frac{1}{x}\) together with line segments parallel to the coordinate axes.
(i) By considering the areas of appropriate rectangles, show that
\[\frac{{2a + 1}}{{a(a + 1)}} < \ln \left( {\frac{{a + 1}}{{a - 1}}} \right) < \frac{{2a - 1}}{{a(a - 1)}}.\]
(ii) Hence find lower and upper bounds for \(\ln (1.2)\).
An improved upper bound can be found by considering Figure 2 which again shows part of the graph of \(y = \frac{1}{x}\).
(i) By considering the areas of appropriate regions, show that
\[\ln \left( {\frac{a}{{a - 1}}} \right) < \frac{{2a - 1}}{{2a(a - 1)}}.\]
(ii) Hence find an upper bound for \(\ln (1.2)\).
Markscheme
(i) the area under the curve between a – 1 and a + 1
\( = \int_{a - 1}^{a + 1} {\frac{{{\text{d}}x}}{x}} \) M1
\( = [\ln x]_{a - 1}^{a + 1}\) A1
\( = \ln \left( {\frac{{a + 1}}{{a - 1}}} \right)\) A1
lower sum \( = \frac{1}{a} + \frac{1}{{a + 1}}\) M1A1
\( = \frac{{2a + 1}}{{a(a + 1)}}\) AG
upper sum \( = \frac{1}{{a - 1}} + \frac{1}{a}\) A1
\( = \frac{{2a - 1}}{{a(a - 1)}}\) AG
it follows that
\(\frac{{2a + 1}}{{a(a + 1)}} < \ln \left( {\frac{{a + 1}}{{a - 1}}} \right) < \frac{{2a - 1}}{{a(a - 1)}}\)
because the area of the region under the curve lies between the areas of the regions defined by the lower and upper sums R1
(ii) putting
\(\left( {\frac{{a + 1}}{{a - 1}} = 1.2} \right) \Rightarrow a = 11\) A1
therefore, \({\text{UB}} = \frac{{21}}{{110}}( = 0.191),{\text{ LB}} = \frac{{23}}{{132}}( = 0.174)\) A1
[9 marks]
(i) the area under the curve between a – 1 and a
\( = \int_{a - 1}^a {\frac{{{\text{d}}x}}{x}} \) A1
\( = [\ln x]_{a - 1}^a = \ln \left( {\frac{a}{{a - 1}}} \right)\)
attempt to find area of trapezium M1
area of trapezoidal “upper sum” \( = \frac{1}{2}\left( {\frac{1}{{a - 1}} + \frac{1}{a}} \right)\) or equivalent A1
\( = \frac{{2a - 1}}{{2a(a - 1)}}\)
it follows that \(\ln \left( {\frac{a}{{a - 1}}} \right) < \frac{{2a - 1}}{{2a(a - 1)}}\) AG
(ii) putting
\(\left( {\frac{a}{{a - 1}} = 1.2} \right) \Rightarrow a = 6\) A1
therefore, \({\text{UB}} = \frac{{11}}{{60}}( = 0.183)\) A1
[5 marks]
Examiners report
Many candidates made progress with this problem. This was pleasing since whilst being relatively straightforward it was not a standard problem. There were still some candidates who did not use the definite integral correctly to find the area under the curve in part (a) and part (b). Also candidates should take care to show all the required working in a “show that” question, even when demonstrating familiar results. The ability to find upper and lower bounds was often well done in parts (a) (ii) and (b) (ii).
Many candidates made progress with this problem. This was pleasing since whilst being relatively straightforward it was not a standard problem. There were still some candidates who did not use the definite integral correctly to find the area under the curve in part (a) and part (b). Also candidates should take care to show all the required working in a “show that” question, even when demonstrating familiar results. The ability to find upper and lower bounds was often well done in parts (a) (ii) and (b) (ii).

