| Date | November 2017 | Marks available | 6 | Reference code | 17N.3ca.hl.TZ0.4 |
| Level | HL only | Paper | Paper 3 Calculus | Time zone | TZ0 |
| Command term | Use and Find | Question number | 4 | Adapted from | N/A |
Question
The mean value theorem states that if \(f\) is a continuous function on \([a,{\text{ }}b]\) and differentiable on \(]a,{\text{ }}b[\) then \(f’(c) = \frac{{f(b) - f(a)}}{{b - a}}\) for some \(c \in ]a,{\text{ }}b[\).
The function \(g\), defined by \(g(x) = x\cos \left( {\sqrt x } \right)\), satisfies the conditions of the mean value theorem on the interval \([0,{\text{ }}5\pi ]\).
For \(a = 0\) and \(b = 5\pi \), use the mean value theorem to find all possible values of \(c\) for the function \(g\).
Sketch the graph of \(y = g(x)\) on the interval \([0,{\text{ }}5\pi ]\) and hence illustrate the mean value theorem for the function \(g\).
Markscheme
\(\frac{{g(5\pi ) - g(0)}}{{5\pi - 0}} = - 0.6809 \ldots {\text{ }}\left( { = \cos \sqrt {5\pi } } \right)\) (gradient of chord) (A1)
\(g’(x) = \cos \left( {\sqrt x } \right) - \frac{{\sqrt x \sin \left( {\sqrt x } \right)}}{2}\) (or equivalent) (M1)(A1)
Note: Award M1 to candidates who attempt to use the product and chain rules.
attempting to solve \(\cos \left( {\sqrt c } \right) - \frac{{\sqrt c \sin \left( {\sqrt c } \right)}}{2} = - 0.6809 \ldots \) for \(c\) (M1)
Notes: Award M1 to candidates who attempt to solve their \(g’(c) = \) gradient of chord.
Do not award M1 to candidates who just attempt to rearrange their equation.
\(c = 2.26,{\text{ }}11.1\) A1A1
Note: Condone candidates working in terms of \(x\).
[6 marks]
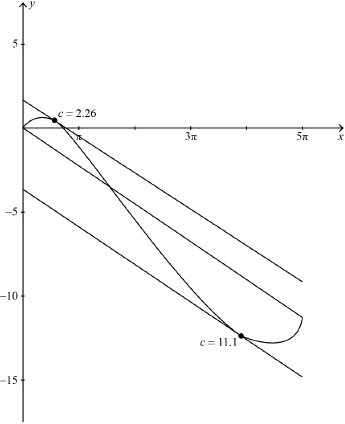
correct graph: 2 turning points close to the endpoints, endpoints indicated and correct endpoint behaviour A1
Notes: Endpoint coordinates are not required. Candidates do not need to indicate axes scales.
correct chord A1
tangents drawn at their values of \(c\) which are approximately parallel to the chord A1A1
Notes: Award A1A0A1A0 to candidates who draw a correct graph, do not draw a chord but draw 2 tangents at their values of \(c\). Condone the absence of their \(c - \) values stated on their sketch. However do not award marks for tangents if no \(c - \) values were found in (a).
[4 marks]

