| Date | November 2015 | Marks available | 2 | Reference code | 15N.3ca.hl.TZ0.5 |
| Level | HL only | Paper | Paper 3 Calculus | Time zone | TZ0 |
| Command term | Show that | Question number | 5 | Adapted from | N/A |
Question
The curves \(y = f(x)\) and \(y = g(x)\) both pass through the point \((1,{\text{ }}0)\) and are defined by the differential equations \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = x - {y^2}\) and \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = y - {x^2}\) respectively.
Show that the tangent to the curve \(y = f(x)\) at the point \((1,{\text{ }}0)\) is normal to the curve \(y = g(x)\) at the point \((1,{\text{ }}0)\).
Find \(g(x)\).
Use Euler’s method with steps of \(0.2\) to estimate \(f(2)\) to \(5\) decimal places.
Explain why \(y = f(x)\) cannot cross the isocline \(x - {y^2} = 0\), for \(x > 1\).
(i) Sketch the isoclines \(x - {y^2} = - 2,{\text{ }}0,{\text{ }}1\).
(ii) On the same set of axes, sketch the graph of \(f\).
Markscheme
gradient of \(f\) at \((1,{\text{ }}0)\) is \(1 - {0^2} = 1\) and the gradient of \(g\) at \((1,{\text{ }}0)\) is \(0 - {1^2} = - 1\) A1
so gradient of normal is \(1\) A1
= Gradient of the tangent of \(f\) at \((1,{\text{ }}0)\) AG
[2 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} - y = - {x^2}\)
integrating factor is \({{\text{e}}^{\int { - 1{\text{d}}x} }} = {{\text{e}}^{ - x}}\) M1
\(y{{\text{e}}^{ - x}} = \int { - {x^2}{{\text{e}}^{ - x}}{\text{d}}x} \) A1
\( = {x^2}{{\text{e}}^{ - x}} - \int {2x{{\text{e}}^{ - x}}{\text{d}}x} \) M1
\( = {x^2}{{\text{e}}^{ - x}} + 2x{{\text{e}}^{ - x}} - \int {2{{\text{e}}^{ - x}}{\text{d}}x} \)
\( = {x^2}{{\text{e}}^{ - x}} + 2x{{\text{e}}^{ - x}} + 2{{\text{e}}^{ - x}} + c\) A1
Note: Condone missing \( + c\) at this stage.
\( \Rightarrow g(x) = {x^2} + 2x + 2 + c{{\text{e}}^x}\)
\(g(1) = 0 \Rightarrow c = - \frac{5}{{\text{e}}}\) M1
\( \Rightarrow g(x) = {x^2} + 2x + 2 - 5{{\text{e}}^{x - 1}}\) A1
[6 marks]
use of \({y_{n + 1}} = {y_n} + hf'({x_n},{\text{ }}{y_n})\) (M1)
\({x_0} = 1,{\text{ }}{y_0} = 0\)
\({x_1} = 1.2,{\text{ }}{y_1} = 0.2\) A1
\({x_2} = 1.4,{\text{ }}{y_2} = 0.432\) (M1)(A1)
\({x_3} = 1.6,{\text{ }}{y_3} = 0.67467 \ldots \)
\({x_4} = 1.8,{\text{ }}{y_4} = 0.90363 \ldots \)
\({x_5} = 2,{\text{ }}{y_5} = 1.1003255 \ldots \)
answer \( = 1.10033\) A1 N3
Note: Award A0 or N1 if \(1.10\) given as answer.
[5 marks]
at the point \((1,{\text{ }}0)\), the gradient of \(f\) is positive so the graph of \(f\) passes into the first quadrant for \(x > 1\)
in the first quadrant below the curve \(x - {y^2} = 0\) the gradient of \(f\) is positive R1
the curve \(x - {y^2} = 0\) has positive gradient in the first quadrant R1
if \(f\) were to reach \(x - {y^2} = 0\) it would have gradient of zero, and therefore would not cross R1
[3 marks]
(i) and (ii)
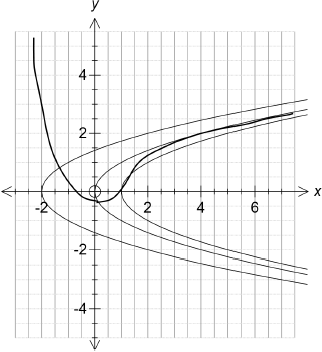 A4
A4
Note: Award A1 for 3 correct isoclines.
Award A1 for \(f\) not reaching \(x - {y^2} = 0\).
Award A1 for turning point of \(f\) on \(x - {y^2} = 0\).
Award A1 for negative gradient to the left of the turning point.
Note: Award A1 for correct shape and position if curve drawn without any isoclines.
[4 marks]
Total [20 marks]

